Accelerated Sampling from Masked Diffusion Models via Entropy Bounded Unmasking

Recent masked diffusion models (MDMs) have shown competitive performance compared to autoregressive models (ARMs) for language modeling. While most literature has focused on performance enhancing sampling procedures, efficient sampling from MDMs has been scarcely explored. We make the observation that often a given sequence of partially masked tokens determines the values of multiple unknown tokens deterministically, meaning that a single prediction of a masked model holds additional information unused by standard sampling procedures. Based on this observation, we introduce EB-Sampler, a simple drop-in replacement for existing samplers, utilizing an Entropy Bounded unmasking procedure that dynamically unmasks multiple tokens in one function evaluation with predefined approximate error tolerance. We formulate the EB-Sampler as part of a broad family of adaptive samplers for which we provide an error analysis that motivates our algorithmic choices. EB-Sampler accelerates sampling from current state of the art MDMs by roughly 2-3x on standard coding and math reasoning benchmarks without loss in performance. We also validate the same procedure works well on smaller reasoning tasks including maze navigation and Sudoku, tasks ARMs often struggle with.

Learning Distributions over Permutations and Rankings with Factorized Representations

Learning distributions over permutations is a fundamental problem in machine learning, with applications in ranking, combinatorial optimization, structured prediction, and data association. Existing methods rely on mixtures of parametric families or neural networks with expensive variational inference procedures. In this work, we propose a novel approach that leverages alternative representations for permutations, including Lehmer codes, Fisher-Yates draws, and Insertion-Vectors. These representations form a bijection with the symmetric group, allowing for unconstrained learning using conventional deep learning techniques, and can represent any probability distribution over permutations. Our approach enables a trade-off between expressivity of the model family and computational requirements. In the least expressive and most computationally efficient case, our method subsumes previous families of well established probabilistic models over permutations, including Mallow's and the Repeated Insertion Model. Experiments indicate our method significantly outperforms current approaches on the jigsaw puzzle benchmark, a common task for permutation learning. However, we argue this benchmark is limited in its ability to assess learning probability distributions, as the target is a delta distribution (i.e., a single correct solution exists). We therefore propose two additional benchmarks: learning cyclic permutations and re-ranking movies based on user preference. We show that our method learns non-trivial distributions even in the least expressive mode, while traditional models fail to even generate valid permutations in this setting.

Flow Matching with General Discrete Paths: A Kinetic-Optimal Perspective

The design space of discrete-space diffusion or flow generative models are significantly less well-understood than their continuous-space counterparts, with many works focusing only on a simple masked construction. In this work, we aim to take a holistic approach to the construction of discrete generative models based on continuous-time Markov chains, and for the first time, allow the use of arbitrary discrete probability paths, or colloquially, corruption processes. Through the lens of optimizing the symmetric kinetic energy, we propose velocity formulas that can be applied to any given probability path, completely decoupling the probability and velocity, and giving the user the freedom to specify any desirable probability path based on expert knowledge specific to the data domain. Furthermore, we find that a special construction of mixture probability paths optimizes the symmetric kinetic energy for the discrete case. We empirically validate the usefulness of this new design space across multiple modalities: text generation, inorganic material generation, and image generation. We find that we can outperform the mask construction even in text with kinetic-optimal mixture paths, while we can make use of domain-specific constructions of the probability path over the visual domain.

Random Cycle Coding: Lossless Compression of Cluster Assignments via Bits-Back Coding

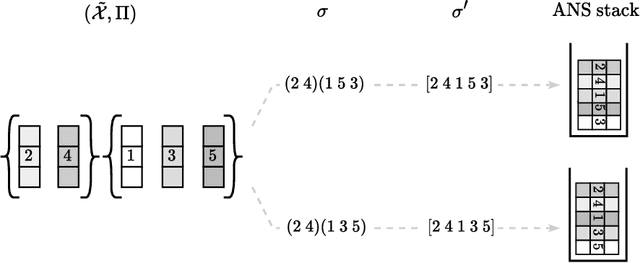
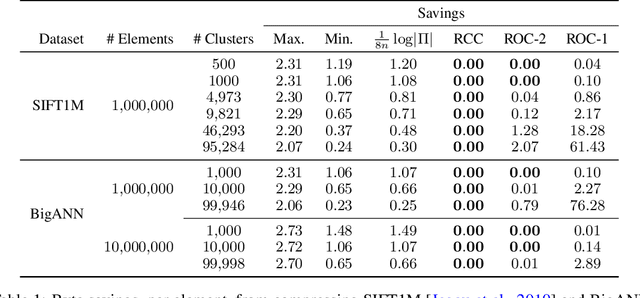
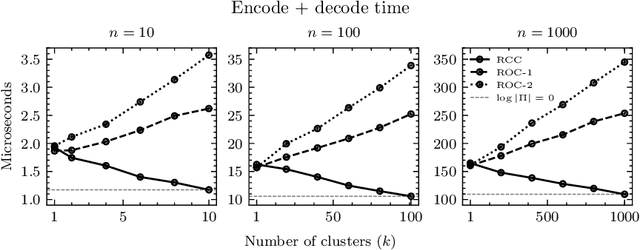
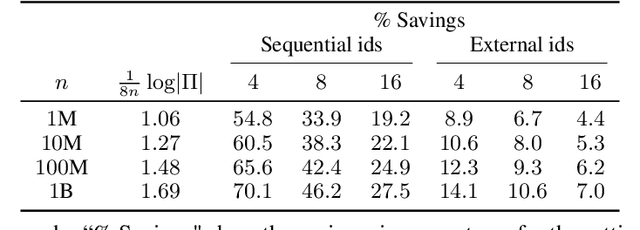
We present an optimal method for encoding cluster assignments of arbitrary data sets. Our method, Random Cycle Coding (RCC), encodes data sequentially and sends assignment information as cycles of the permutation defined by the order of encoded elements. RCC does not require any training and its worst-case complexity scales quasi-linearly with the size of the largest cluster. We characterize the achievable bit rates as a function of cluster sizes and number of elements, showing RCC consistently outperforms previous methods while requiring less compute and memory resources. Experiments show RCC can save up to 2 bytes per element when applied to vector databases, and removes the need for assigning integer ids to identify vectors, translating to savings of up to 70% in vector database systems for similarity search applications.

Random Permutation Codes: Lossless Source Coding of Non-Sequential Data

This thesis deals with the problem of communicating and storing non-sequential data. We investigate this problem through the lens of lossless source coding, also sometimes referred to as lossless compression, from both an algorithmic and information-theoretic perspective. Lossless compression algorithms typically preserve the ordering in which data points are compressed. However, there are data types where order is not meaningful, such as collections of files, rows in a database, nodes in a graph, and, notably, datasets in machine learning applications. Compressing with traditional algorithms is possible if we pick an order for the elements and communicate the corresponding ordered sequence. However, unless the order information is somehow removed during the encoding process, this procedure will be sub-optimal, because the order contains information and therefore more bits are used to represent the source than are truly necessary. In this work we give a formal definition for non-sequential objects as random sets of equivalent sequences, which we refer to as Combinatorial Random Variables (CRVs). The definition of equivalence, formalized as an equivalence relation, establishes the non-sequential data type represented by the CRV. The achievable rates of CRVs is fully characterized as a function of the equivalence relation as well as the data distribution. The optimal rates of CRVs are achieved within the family of Random Permutation Codes (RPCs) developed in later chapters. RPCs randomly select one-of-many possible sequences that can represent the instance of the CRV. Specialized RPCs are given for the case of multisets, graphs, and partitions/clusterings, providing new algorithms for compression of databases, social networks, and web data in the JSON file format.

Entropy Coding of Unordered Data Structures

We present shuffle coding, a general method for optimal compression of sequences of unordered objects using bits-back coding. Data structures that can be compressed using shuffle coding include multisets, graphs, hypergraphs, and others. We release an implementation that can easily be adapted to different data types and statistical models, and demonstrate that our implementation achieves state-of-the-art compression rates on a range of graph datasets including molecular data.

The Unreasonable Effectiveness of Linear Prediction as a Perceptual Metric

We show how perceptual embeddings of the visual system can be constructed at inference-time with no training data or deep neural network features. Our perceptual embeddings are solutions to a weighted least squares (WLS) problem, defined at the pixel-level, and solved at inference-time, that can capture global and local image characteristics. The distance in embedding space is used to define a perceptual similarity metric which we call LASI: Linear Autoregressive Similarity Index. Experiments on full-reference image quality assessment datasets show LASI performs competitively with learned deep feature based methods like LPIPS (Zhang et al., 2018) and PIM (Bhardwaj et al., 2020), at a similar computational cost to hand-crafted methods such as MS-SSIM (Wang et al., 2003). We found that increasing the dimensionality of the embedding space consistently reduces the WLS loss while increasing performance on perceptual tasks, at the cost of increasing the computational complexity. LASI is fully differentiable, scales cubically with the number of embedding dimensions, and can be parallelized at the pixel-level. A Maximum Differentiation (MAD) competition (Wang & Simoncelli, 2008) between LASI and LPIPS shows that both methods are capable of finding failure points for the other, suggesting these metrics can be combined.

Random Edge Coding: One-Shot Bits-Back Coding of Large Labeled Graphs

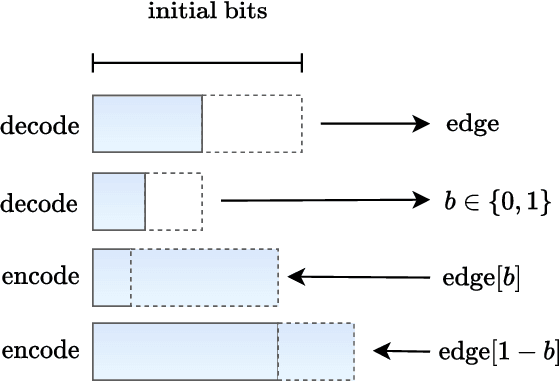
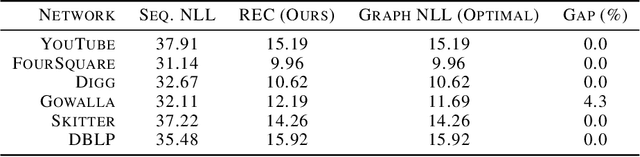
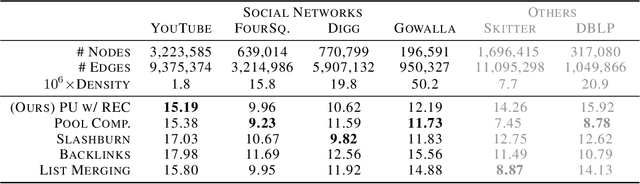
We present a one-shot method for compressing large labeled graphs called Random Edge Coding. When paired with a parameter-free model based on P\'olya's Urn, the worst-case computational and memory complexities scale quasi-linearly and linearly with the number of observed edges, making it efficient on sparse graphs, and requires only integer arithmetic. Key to our method is bits-back coding, which is used to sample edges and vertices without replacement from the edge-list in a way that preserves the structure of the graph. Optimality is proven under a class of random graph models that are invariant to permutations of the edges and of vertices within an edge. Experiments indicate Random Edge Coding can achieve competitive compression performance on real-world network datasets and scales to graphs with millions of nodes and edges.

Action Matching: A Variational Method for Learning Stochastic Dynamics from Samples

Stochastic dynamics are ubiquitous in many fields of science, from the evolution of quantum systems in physics to diffusion-based models in machine learning. Existing methods such as score matching can be used to simulate these physical processes by assuming that the dynamics is a diffusion, which is not always the case. In this work, we propose a method called "Action Matching" that enables us to learn a much broader family of stochastic dynamics. Our method requires access only to samples from different time-steps, makes no explicit assumptions about the underlying dynamics, and can be applied even when samples are uncorrelated (i.e., are not part of a trajectory). Action Matching directly learns an underlying mechanism to move samples in time without modeling the distributions at each time-step. In this work, we showcase how Action Matching can be used for several computer vision tasks such as generative modeling, super-resolution, colorization, and inpainting; and further discuss potential applications in other areas of science.

Compressing Multisets with Large Alphabets

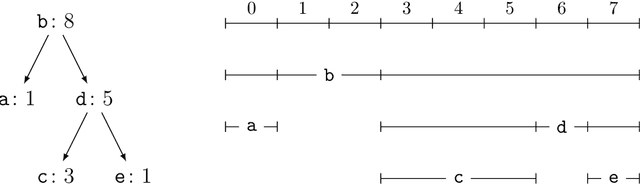
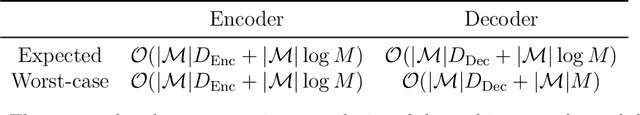
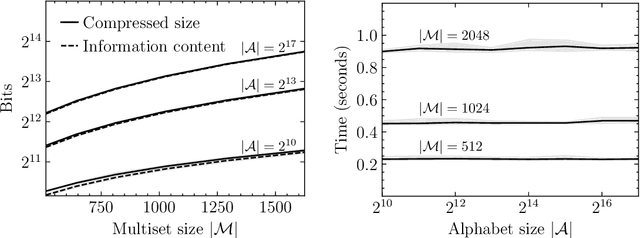
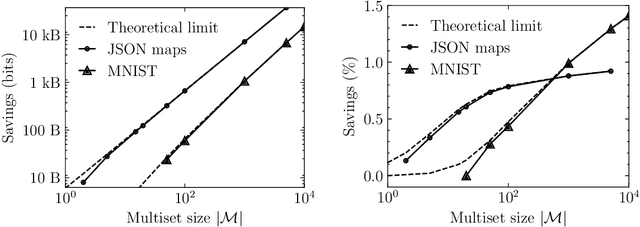
Current methods that optimally compress multisets are not suitable for high-dimensional symbols, as their compute time scales linearly with alphabet size. Compressing a multiset as an ordered sequence with off-the-shelf codecs is computationally more efficient, but has a sub-optimal compression rate, as bits are wasted encoding the order between symbols. We present a method that can recover those bits, assuming symbols are i.i.d., at the cost of an additional $\mathcal{O}(|\mathcal{M}|\log M)$ in average time complexity, where $|\mathcal{M}|$ and $M$ are the total and unique number of symbols in the multiset. Our method is compatible with any prefix-free code. Experiments show that, when paired with efficient coders, our method can efficiently compress high-dimensional sources such as multisets of images and collections of JSON files.