Gumbel-max List Sampling for Distribution Coupling with Multiple Samples

We study a relaxation of the problem of coupling probability distributions -- a list of samples is generated from one distribution and an accept is declared if any one of these samples is identical to the sample generated from the other distribution. We propose a novel method for generating samples, which extends the Gumbel-max sampling suggested in Daliri et al. (arXiv:2408.07978) for coupling probability distributions. We also establish a corresponding lower bound on the acceptance probability, which we call the list matching lemma. We next discuss two applications of our setup. First, we develop a new mechanism for multi-draft speculative sampling that is simple to implement and achieves performance competitive with baselines such as SpecTr and SpecInfer across a range of language tasks. Our method also guarantees a certain degree of drafter invariance with respect to the output tokens which is not supported by existing schemes. We also provide a theoretical lower bound on the token level acceptance probability. As our second application, we consider distributed lossy compression with side information in a setting where a source sample is compressed and available to multiple decoders, each with independent side information. We propose a compression technique that is based on our generalization of Gumbel-max sampling and show that it provides significant gains in experiments involving synthetic Gaussian sources and the MNIST image dataset.

List-Level Distribution Coupling with Applications to Speculative Decoding and Lossy Compression

We study a relaxation of the problem of coupling probability distributions -- a list of samples is generated from one distribution and an accept is declared if any one of these samples is identical to the sample generated from the other distribution. We propose a novel method for generating samples, which extends the Gumbel-max sampling suggested in Daliri et al. (arXiv:2408.07978) for coupling probability distributions. We also establish a corresponding lower bound on the acceptance probability, which we call the list matching lemma. We next discuss two applications of our setup. First, we develop a new mechanism for multi-draft speculative sampling that is simple to implement and achieves performance competitive with baselines such as SpecTr and SpecInfer across a range of language tasks. Our method also guarantees a certain degree of drafter invariance with respect to the output tokens which is not supported by existing schemes. We also provide a theoretical lower bound on the token level acceptance probability. As our second application, we consider distributed lossy compression with side information in a setting where a source sample is compressed and available to multiple decoders, each with independent side information. We propose a compression technique that is based on our generalization of Gumbel-max sampling and show that it provides significant gains in experiments involving synthetic Gaussian sources and the MNIST image dataset.

Robust Federated Finetuning of LLMs via Alternating Optimization of LoRA

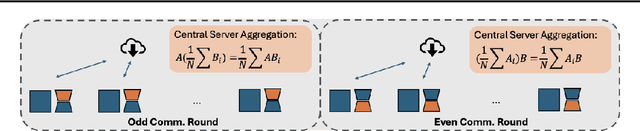
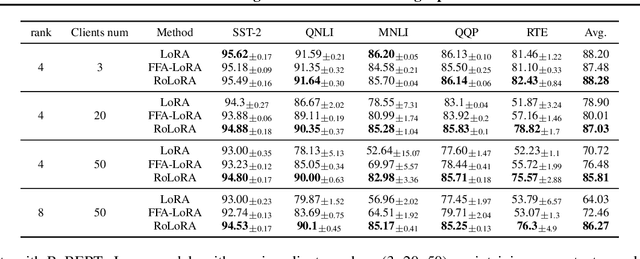
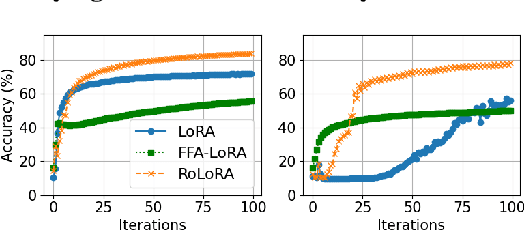
Parameter-Efficient Fine-Tuning (PEFT) methods like Low-Rank Adaptation (LoRA) optimize federated training by reducing computational and communication costs. We propose RoLoRA, a federated framework using alternating optimization to fine-tune LoRA adapters. Our approach emphasizes the importance of learning up and down projection matrices to enhance expressiveness and robustness. We use both theoretical analysis and extensive experiments to demonstrate the advantages of RoLoRA over prior approaches that either generate imperfect model updates or limit expressiveness of the model. We present theoretical analysis on a simplified linear model to demonstrate the importance of learning both down-projection and up-projection matrices in LoRA. We provide extensive experimental evaluations on a toy neural network on MNIST as well as large language models including RoBERTa-Large, Llama-2-7B on diverse tasks to demonstrate the advantages of RoLoRA over other methods.

Random Cycle Coding: Lossless Compression of Cluster Assignments via Bits-Back Coding

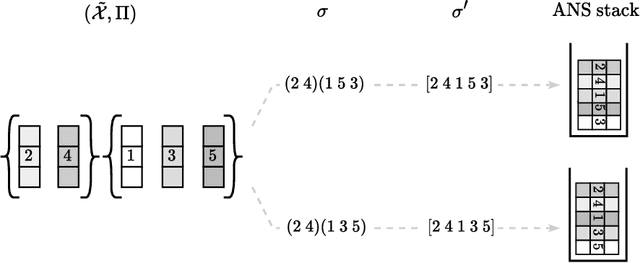
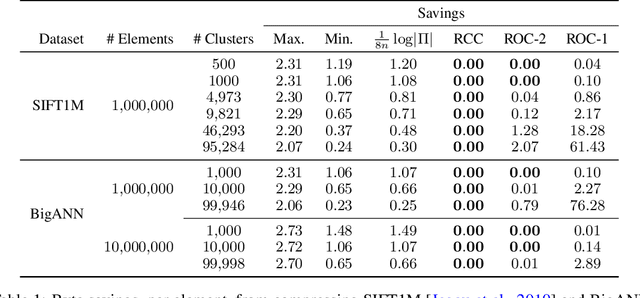
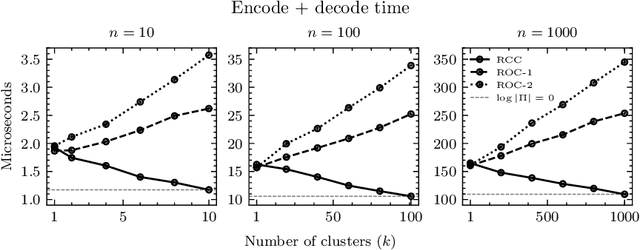
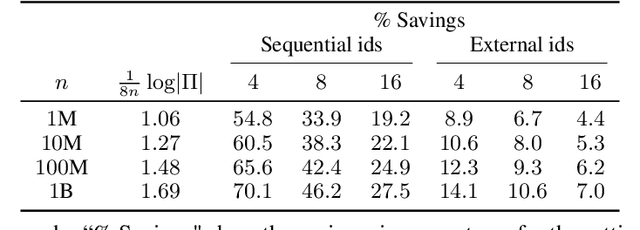
We present an optimal method for encoding cluster assignments of arbitrary data sets. Our method, Random Cycle Coding (RCC), encodes data sequentially and sends assignment information as cycles of the permutation defined by the order of encoded elements. RCC does not require any training and its worst-case complexity scales quasi-linearly with the size of the largest cluster. We characterize the achievable bit rates as a function of cluster sizes and number of elements, showing RCC consistently outperforms previous methods while requiring less compute and memory resources. Experiments show RCC can save up to 2 bytes per element when applied to vector databases, and removes the need for assigning integer ids to identify vectors, translating to savings of up to 70% in vector database systems for similarity search applications.

Minimum Entropy Coupling with Bottleneck

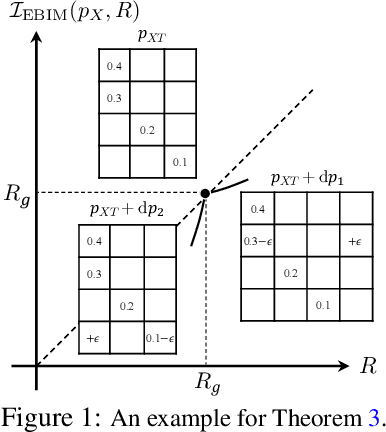
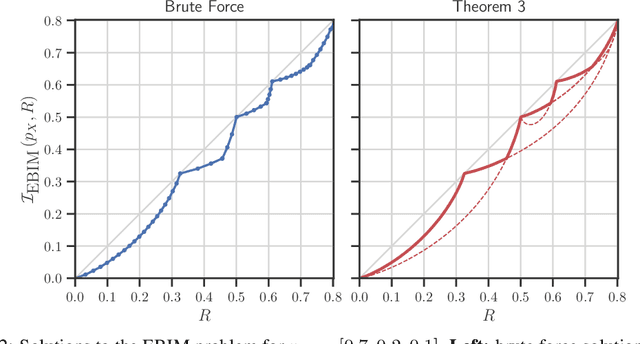
This paper investigates a novel lossy compression framework operating under logarithmic loss, designed to handle situations where the reconstruction distribution diverges from the source distribution. This framework is especially relevant for applications that require joint compression and retrieval, and in scenarios involving distributional shifts due to processing. We show that the proposed formulation extends the classical minimum entropy coupling framework by integrating a bottleneck, allowing for a controlled degree of stochasticity in the coupling. We explore the decomposition of the Minimum Entropy Coupling with Bottleneck (MEC-B) into two distinct optimization problems: Entropy-Bounded Information Maximization (EBIM) for the encoder, and Minimum Entropy Coupling (MEC) for the decoder. Through extensive analysis, we provide a greedy algorithm for EBIM with guaranteed performance, and characterize the optimal solution near functional mappings, yielding significant theoretical insights into the structural complexity of this problem. Furthermore, we illustrate the practical application of MEC-B through experiments in Markov Coding Games (MCGs) under rate limits. These games simulate a communication scenario within a Markov Decision Process, where an agent must transmit a compressed message from a sender to a receiver through its actions. Our experiments highlight the trade-offs between MDP rewards and receiver accuracy across various compression rates, showcasing the efficacy of our method compared to conventional compression baseline.

Multi-Draft Speculative Sampling: Canonical Architectures and Theoretical Limits

We consider multi-draft speculative sampling, where the proposal sequences are sampled independently from different draft models. At each step, a token-level draft selection scheme takes a list of valid tokens as input and produces an output token whose distribution matches that of the target model. Previous works have demonstrated that the optimal scheme (which maximizes the probability of accepting one of the input tokens) can be cast as a solution to a linear program. In this work we show that the optimal scheme can be decomposed into a two-step solution: in the first step an importance sampling (IS) type scheme is used to select one intermediate token; in the second step (single-draft) speculative sampling is applied to generate the output token. For the case of two identical draft models we further 1) establish a necessary and sufficient condition on the distributions of the target and draft models for the acceptance probability to equal one and 2) provide an explicit expression for the optimal acceptance probability. Our theoretical analysis also motives a new class of token-level selection scheme based on weighted importance sampling. Our experimental results demonstrate consistent improvements in the achievable block efficiency and token rates over baseline schemes in a number of scenarios.

Robust Federated Finetuning of Foundation Models via Alternating Minimization of LoRA

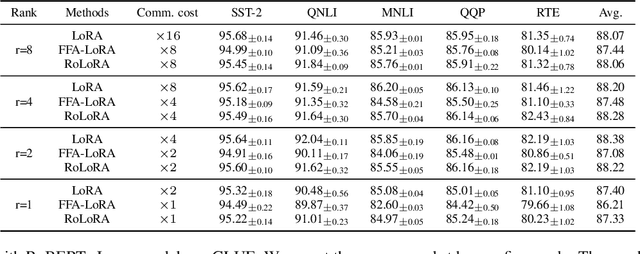
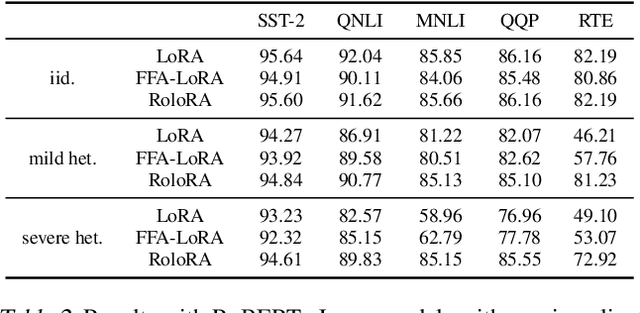
Parameter-Efficient Fine-Tuning (PEFT) has risen as an innovative training strategy that updates only a select few model parameters, significantly lowering both computational and memory demands. PEFT also helps to decrease data transfer in federated learning settings, where communication depends on the size of updates. In this work, we explore the constraints of previous studies that integrate a well-known PEFT method named LoRA with federated fine-tuning, then introduce RoLoRA, a robust federated fine-tuning framework that utilizes an alternating minimization approach for LoRA, providing greater robustness against decreasing fine-tuning parameters and increasing data heterogeneity. Our results indicate that RoLoRA not only presents the communication benefits but also substantially enhances the robustness and effectiveness in multiple federated fine-tuning scenarios.

Rate-Distortion-Perception Tradeoff Based on the Conditional-Distribution Perception Measure

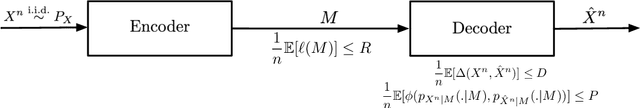
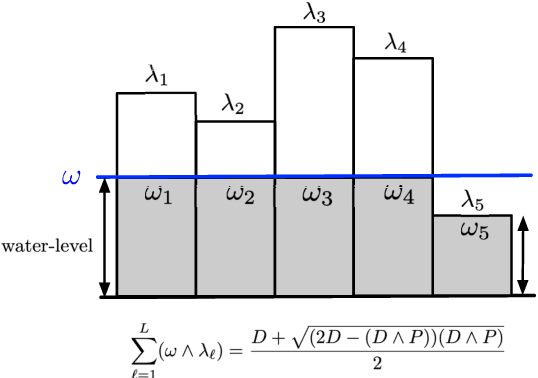
We study the rate-distortion-perception (RDP) tradeoff for a memoryless source model in the asymptotic limit of large block-lengths. Our perception measure is based on a divergence between the distributions of the source and reconstruction sequences conditioned on the encoder output, which was first proposed in [1], [2]. We consider the case when there is no shared randomness between the encoder and the decoder. For the case of discrete memoryless sources we derive a single-letter characterization of the RDP function, thus settling a problem that remains open for the marginal metric introduced in Blau and Michaeli [3] (with no shared randomness). Our achievability scheme is based on lossy source coding with a posterior reference map proposed in [4]. For the case of continuous valued sources under squared error distortion measure and squared quadratic Wasserstein perception measure we also derive a single-letter characterization and show that a noise-adding mechanism at the decoder suffices to achieve the optimal representation. For the case of zero perception loss, we show that our characterization interestingly coincides with the results for the marginal metric derived in [5], [6] and again demonstrate that zero perception loss can be achieved with a $3$-dB penalty in the minimum distortion. Finally we specialize our results to the case of Gaussian sources. We derive the RDP function for vector Gaussian sources and propose a waterfilling type solution. We also partially characterize the RDP function for a mixture of vector Gaussians.

On the Choice of Perception Loss Function for Learned Video Compression

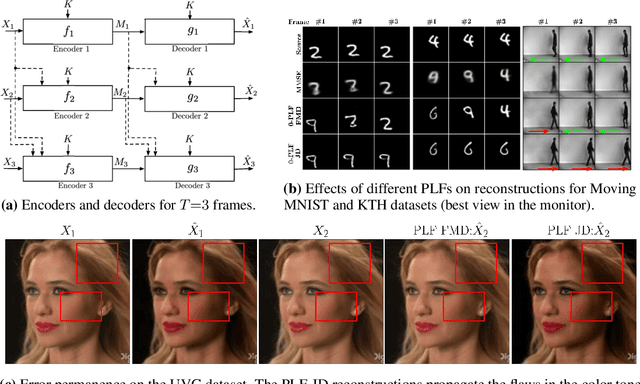
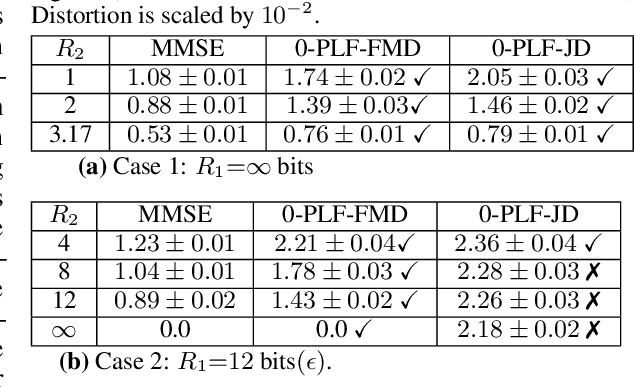
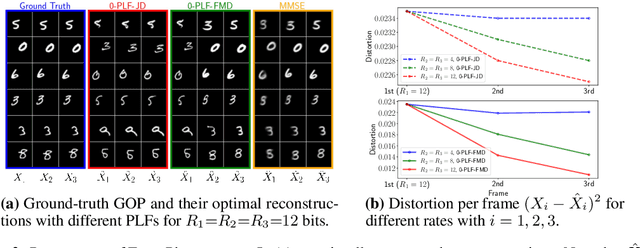
We study causal, low-latency, sequential video compression when the output is subjected to both a mean squared-error (MSE) distortion loss as well as a perception loss to target realism. Motivated by prior approaches, we consider two different perception loss functions (PLFs). The first, PLF-JD, considers the joint distribution (JD) of all the video frames up to the current one, while the second metric, PLF-FMD, considers the framewise marginal distributions (FMD) between the source and reconstruction. Using information theoretic analysis and deep-learning based experiments, we demonstrate that the choice of PLF can have a significant effect on the reconstruction, especially at low-bit rates. In particular, while the reconstruction based on PLF-JD can better preserve the temporal correlation across frames, it also imposes a significant penalty in distortion compared to PLF-FMD and further makes it more difficult to recover from errors made in the earlier output frames. Although the choice of PLF decisively affects reconstruction quality, we also demonstrate that it may not be essential to commit to a particular PLF during encoding and the choice of PLF can be delegated to the decoder. In particular, encoded representations generated by training a system to minimize the MSE (without requiring either PLF) can be {\em near universal} and can generate close to optimal reconstructions for either choice of PLF at the decoder. We validate our results using (one-shot) information-theoretic analysis, detailed study of the rate-distortion-perception tradeoff of the Gauss-Markov source model as well as deep-learning based experiments on moving MNIST and KTH datasets.

Random Edge Coding: One-Shot Bits-Back Coding of Large Labeled Graphs

We present a one-shot method for compressing large labeled graphs called Random Edge Coding. When paired with a parameter-free model based on P\'olya's Urn, the worst-case computational and memory complexities scale quasi-linearly and linearly with the number of observed edges, making it efficient on sparse graphs, and requires only integer arithmetic. Key to our method is bits-back coding, which is used to sample edges and vertices without replacement from the edge-list in a way that preserves the structure of the graph. Optimality is proven under a class of random graph models that are invariant to permutations of the edges and of vertices within an edge. Experiments indicate Random Edge Coding can achieve competitive compression performance on real-world network datasets and scales to graphs with millions of nodes and edges.