Entropy Coding of Unordered Data Structures

We present shuffle coding, a general method for optimal compression of sequences of unordered objects using bits-back coding. Data structures that can be compressed using shuffle coding include multisets, graphs, hypergraphs, and others. We release an implementation that can easily be adapted to different data types and statistical models, and demonstrate that our implementation achieves state-of-the-art compression rates on a range of graph datasets including molecular data.

Random Edge Coding: One-Shot Bits-Back Coding of Large Labeled Graphs

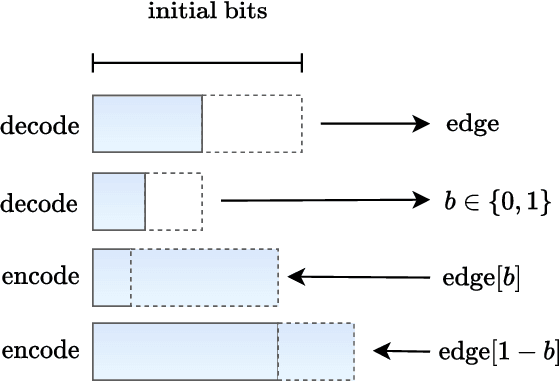
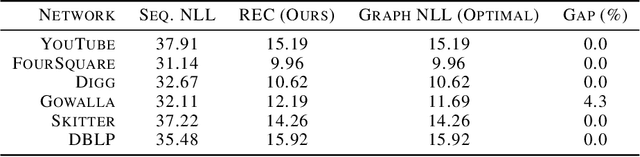
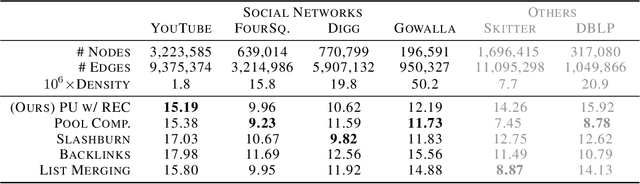
We present a one-shot method for compressing large labeled graphs called Random Edge Coding. When paired with a parameter-free model based on P\'olya's Urn, the worst-case computational and memory complexities scale quasi-linearly and linearly with the number of observed edges, making it efficient on sparse graphs, and requires only integer arithmetic. Key to our method is bits-back coding, which is used to sample edges and vertices without replacement from the edge-list in a way that preserves the structure of the graph. Optimality is proven under a class of random graph models that are invariant to permutations of the edges and of vertices within an edge. Experiments indicate Random Edge Coding can achieve competitive compression performance on real-world network datasets and scales to graphs with millions of nodes and edges.

Verified Reversible Programming for Verified Lossless Compression

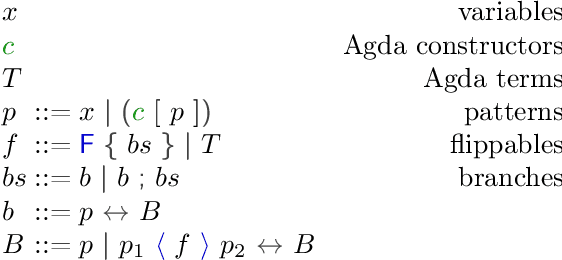
Lossless compression implementations typically contain two programs, an encoder and a decoder, which are required to be inverse to one another. Maintaining consistency between two such programs during development requires care, and incorrect data decoding can be costly and difficult to debug. We observe that a significant class of compression methods, based on asymmetric numeral systems (ANS), have shared structure between the encoder and decoder -- the decoder program is the 'reverse' of the encoder program -- allowing both to be simultaneously specified by a single, reversible, 'codec' function. To exploit this, we have implemented a small reversible language, embedded in Agda, which we call 'Flipper'. Agda supports formal verification of program properties, and the compiler for our reversible language (which is implemented as an Agda macro), produces not just an encoder/decoder pair of functions but also a proof that they are inverse to one another. Thus users of the language get formal verification 'for free'. We give a small example use-case of Flipper in this paper, and plan to publish a full compression implementation soon.

Parallel Neural Local Lossless Compression

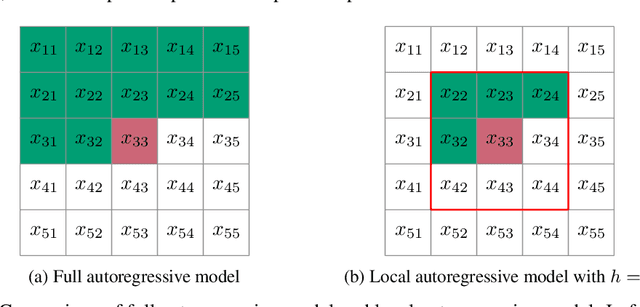
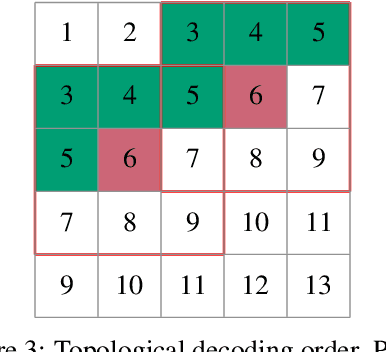
The recently proposed Neural Local Lossless Compression (NeLLoC), which is based on a local autoregressive model, has achieved state-of-the-art (SOTA) out-of-distribution (OOD) generalization performance in the image compression task. In addition to the encouragement of OOD generalization, the local model also allows parallel inference in the decoding stage. In this paper, we propose a parallelization scheme for local autoregressive models. We discuss the practicalities of implementing this scheme, and provide experimental evidence of significant gains in compression runtime compared to the previous, non-parallel implementation.

Adaptive Optimization with Examplewise Gradients

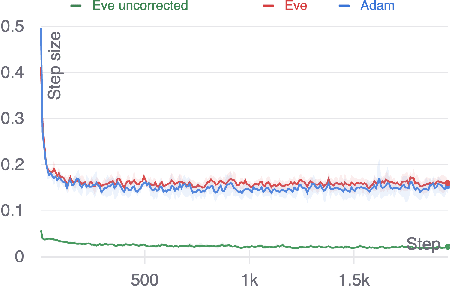
We propose a new, more general approach to the design of stochastic gradient-based optimization methods for machine learning. In this new framework, optimizers assume access to a batch of gradient estimates per iteration, rather than a single estimate. This better reflects the information that is actually available in typical machine learning setups. To demonstrate the usefulness of this generalized approach, we develop Eve, an adaptation of the Adam optimizer which uses examplewise gradients to obtain more accurate second-moment estimates. We provide preliminary experiments, without hyperparameter tuning, which show that the new optimizer slightly outperforms Adam on a small scale benchmark and performs the same or worse on larger scale benchmarks. Further work is needed to refine the algorithm and tune hyperparameters.

Compressing Multisets with Large Alphabets

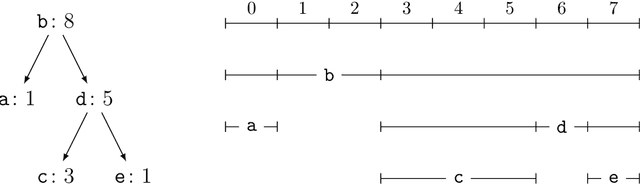
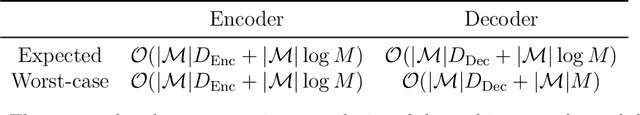
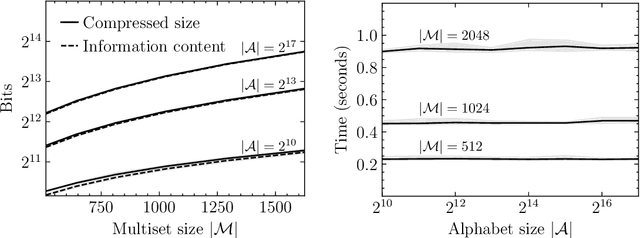
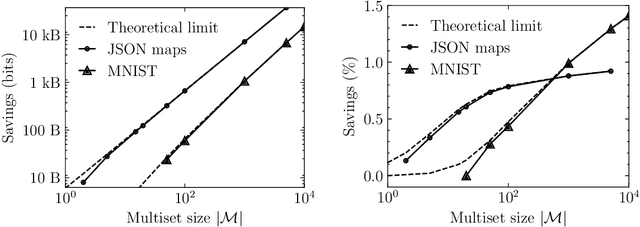
Current methods that optimally compress multisets are not suitable for high-dimensional symbols, as their compute time scales linearly with alphabet size. Compressing a multiset as an ordered sequence with off-the-shelf codecs is computationally more efficient, but has a sub-optimal compression rate, as bits are wasted encoding the order between symbols. We present a method that can recover those bits, assuming symbols are i.i.d., at the cost of an additional $\mathcal{O}(|\mathcal{M}|\log M)$ in average time complexity, where $|\mathcal{M}|$ and $M$ are the total and unique number of symbols in the multiset. Our method is compatible with any prefix-free code. Experiments show that, when paired with efficient coders, our method can efficiently compress high-dimensional sources such as multisets of images and collections of JSON files.

Lossless Compression with Latent Variable Models

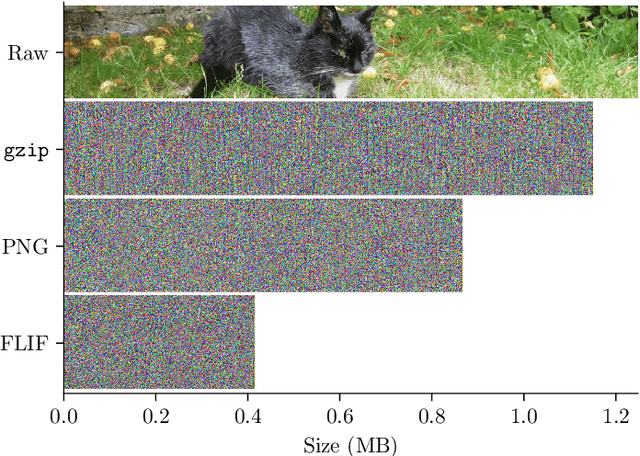
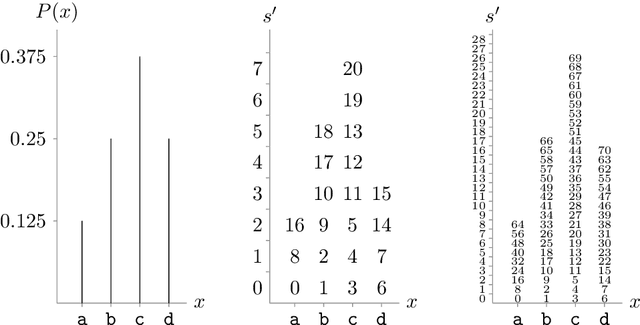
We develop a simple and elegant method for lossless compression using latent variable models, which we call 'bits back with asymmetric numeral systems' (BB-ANS). The method involves interleaving encode and decode steps, and achieves an optimal rate when compressing batches of data. We demonstrate it firstly on the MNIST test set, showing that state-of-the-art lossless compression is possible using a small variational autoencoder (VAE) model. We then make use of a novel empirical insight, that fully convolutional generative models, trained on small images, are able to generalize to images of arbitrary size, and extend BB-ANS to hierarchical latent variable models, enabling state-of-the-art lossless compression of full-size colour images from the ImageNet dataset. We describe 'Craystack', a modular software framework which we have developed for rapid prototyping of compression using deep generative models.

Lossless compression with state space models using bits back coding

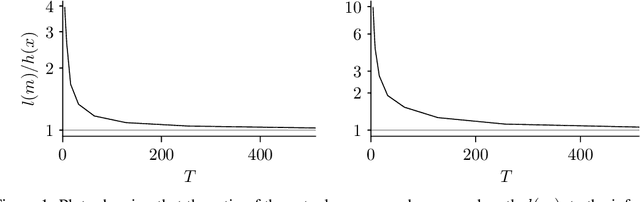
We generalize the 'bits back with ANS' method to time-series models with a latent Markov structure. This family of models includes hidden Markov models (HMMs), linear Gaussian state space models (LGSSMs) and many more. We provide experimental evidence that our method is effective for small scale models, and discuss its applicability to larger scale settings such as video compression.

Improving Lossless Compression Rates via Monte Carlo Bits-Back Coding

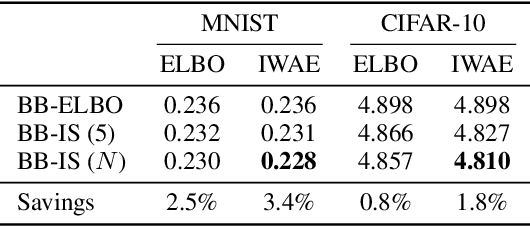
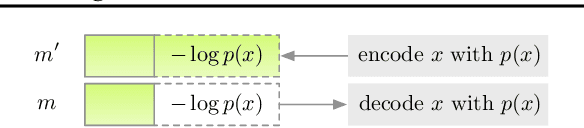
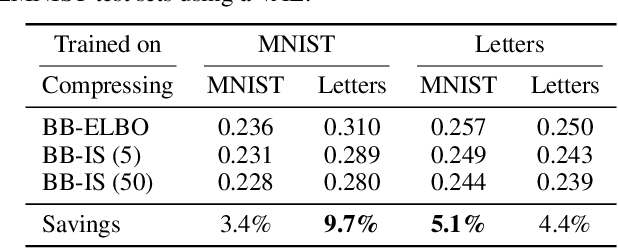
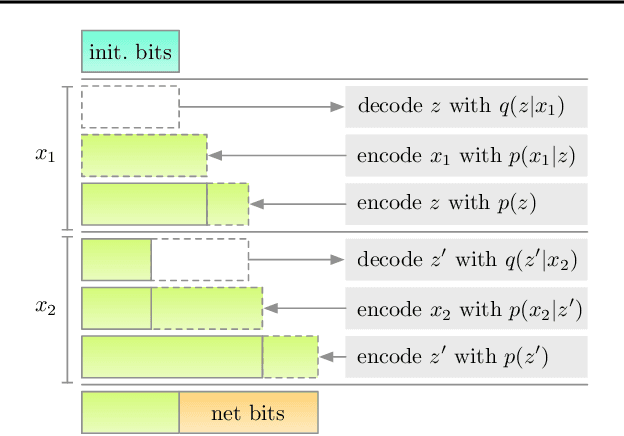
Latent variable models have been successfully applied in lossless compression with the bits-back coding algorithm. However, bits-back suffers from an increase in the bitrate equal to the KL divergence between the approximate posterior and the true posterior. In this paper, we show how to remove this gap asymptotically by deriving bits-back coding algorithms from tighter variational bounds. The key idea is to exploit extended space representations of Monte Carlo estimators of the marginal likelihood. Naively applied, our schemes would require more initial bits than the standard bits-back coder, but we show how to drastically reduce this additional cost with couplings in the latent space. When parallel architectures can be exploited, our coders can achieve better rates than bits-back with little additional cost. We demonstrate improved lossless compression rates in a variety of settings, including entropy coding for lossy compression.

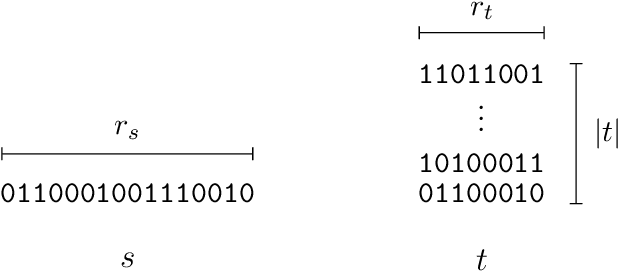
A tutorial on the range variant of asymmetric numeral systems

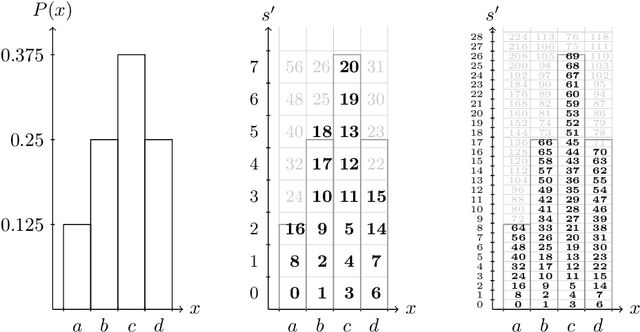
This paper is intended to be an accessible introduction to the range variant of Asymmetric Numeral Systems (rANS). This version of ANS can be used as a drop in replacement for traditional arithmetic coding (AC). Implementing rANS is more straightforward than AC, and this paper includes pseudo-code which could be converted without too much effort into a working implementation. An example implementation, based on this tutorial, is available at https://raw.githubusercontent.com/j-towns/ans-notes/master/rans.py. After reading (and understanding) this tutorial, the reader should understand how rANS works, and be able to implement it and prove that it attains a near optimal compression rate.