Random Edge Coding: One-Shot Bits-Back Coding of Large Labeled Graphs
Paper and Code
May 16, 2023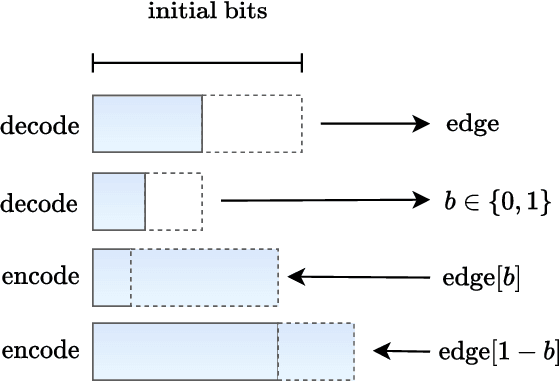
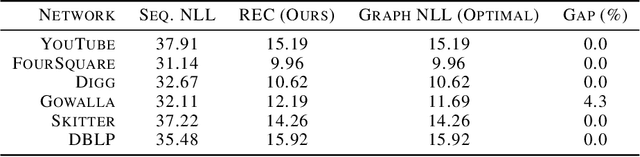

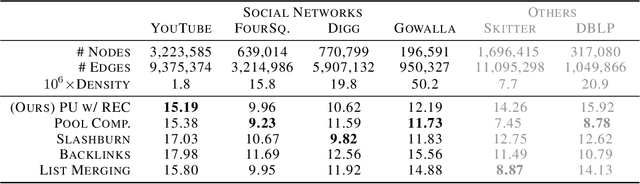
We present a one-shot method for compressing large labeled graphs called Random Edge Coding. When paired with a parameter-free model based on P\'olya's Urn, the worst-case computational and memory complexities scale quasi-linearly and linearly with the number of observed edges, making it efficient on sparse graphs, and requires only integer arithmetic. Key to our method is bits-back coding, which is used to sample edges and vertices without replacement from the edge-list in a way that preserves the structure of the graph. Optimality is proven under a class of random graph models that are invariant to permutations of the edges and of vertices within an edge. Experiments indicate Random Edge Coding can achieve competitive compression performance on real-world network datasets and scales to graphs with millions of nodes and edges.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge