Lossless compression with state space models using bits back coding

We generalize the 'bits back with ANS' method to time-series models with a latent Markov structure. This family of models includes hidden Markov models (HMMs), linear Gaussian state space models (LGSSMs) and many more. We provide experimental evidence that our method is effective for small scale models, and discuss its applicability to larger scale settings such as video compression.

Density Deconvolution with Normalizing Flows

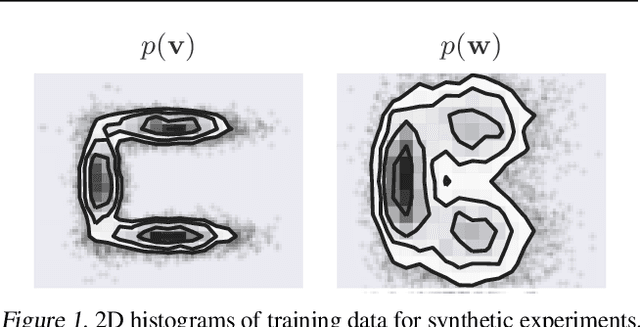
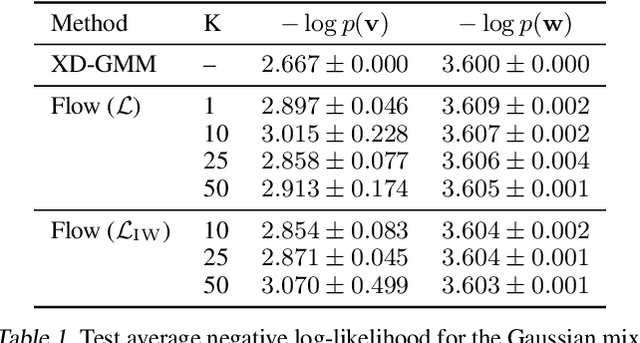
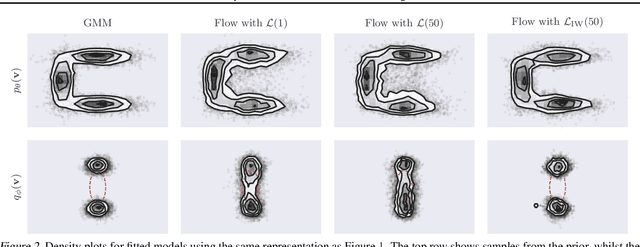
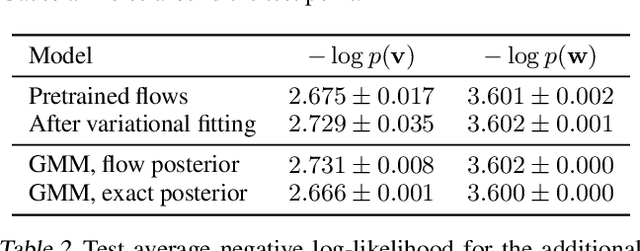
Density deconvolution is the task of estimating a probability density function given only noise-corrupted samples. We can fit a Gaussian mixture model to the underlying density by maximum likelihood if the noise is normally distributed, but would like to exploit the superior density estimation performance of normalizing flows and allow for arbitrary noise distributions. Since both adjustments lead to an intractable likelihood, we resort to amortized variational inference. We demonstrate some problems involved in this approach, however, experiments on real data demonstrate that flows can already out-perform Gaussian mixtures for density deconvolution.

Diverse Ensembles Improve Calibration

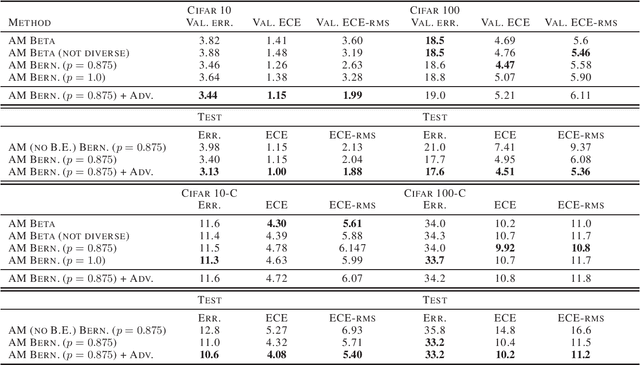
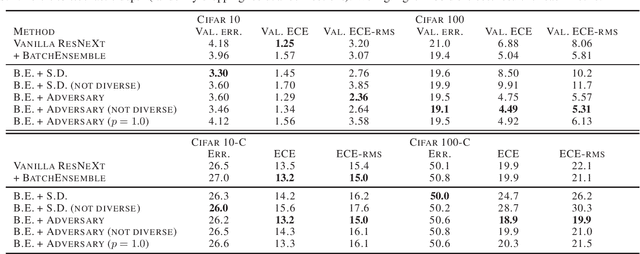
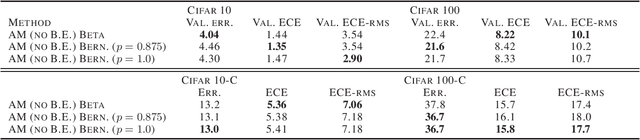
Modern deep neural networks can produce badly calibrated predictions, especially when train and test distributions are mismatched. Training an ensemble of models and averaging their predictions can help alleviate these issues. We propose a simple technique to improve calibration, using a different data augmentation for each ensemble member. We additionally use the idea of `mixing' un-augmented and augmented inputs to improve calibration when test and training distributions are the same. These simple techniques improve calibration and accuracy over strong baselines on the CIFAR10 and CIFAR100 benchmarks, and out-of-domain data from their corrupted versions.

Ordering Dimensions with Nested Dropout Normalizing Flows

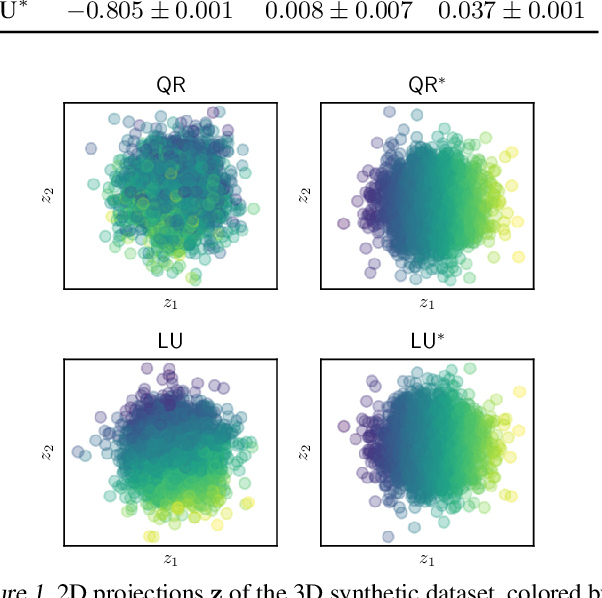
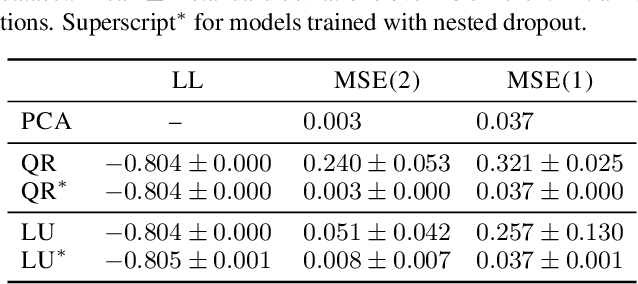
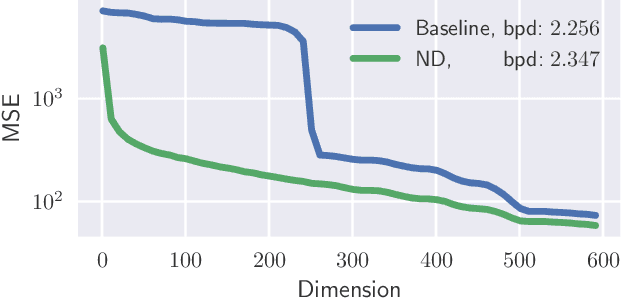
The latent space of normalizing flows must be of the same dimensionality as their output space. This constraint presents a problem if we want to learn low-dimensional, semantically meaningful representations. Recent work has provided compact representations by fitting flows constrained to manifolds, but hasn't defined a density off that manifold. In this work we consider flows with full support in data space, but with ordered latent variables. Like in PCA, the leading latent dimensions define a sequence of manifolds that lie close to the data. We note a trade-off between the flow likelihood and the quality of the ordering, depending on the parameterization of the flow.

On Contrastive Learning for Likelihood-free Inference

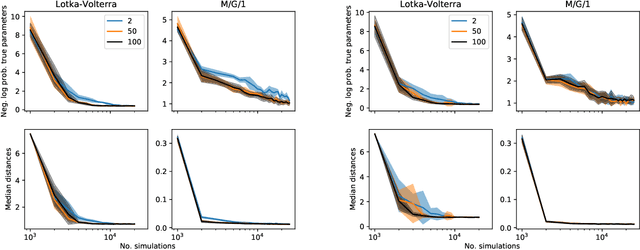
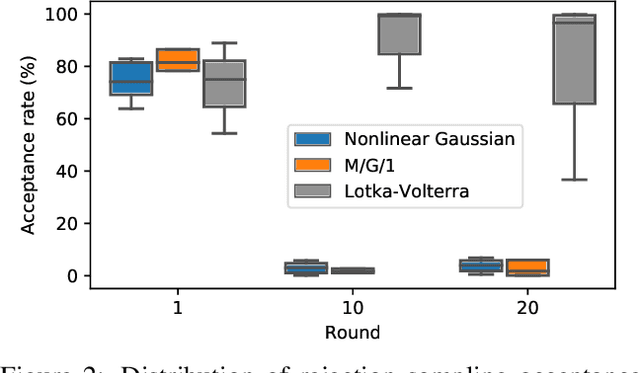
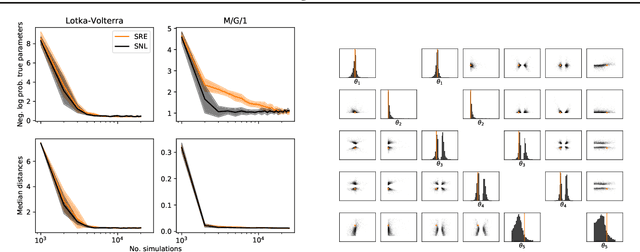
Likelihood-free methods perform parameter inference in stochastic simulator models where evaluating the likelihood is intractable but sampling synthetic data is possible. One class of methods for this likelihood-free problem uses a classifier to distinguish between pairs of parameter-observation samples generated using the simulator and pairs sampled from some reference distribution, which implicitly learns a density ratio proportional to the likelihood. Another popular class of methods fits a conditional distribution to the parameter posterior directly, and a particular recent variant allows for the use of flexible neural density estimators for this task. In this work, we show that both of these approaches can be unified under a general contrastive learning scheme, and clarify how they should be run and compared.

Scalable Extreme Deconvolution

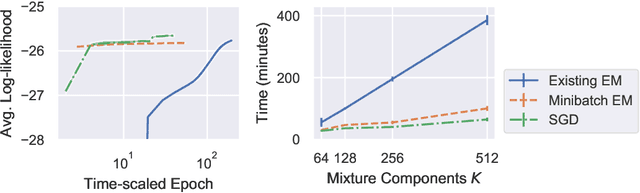
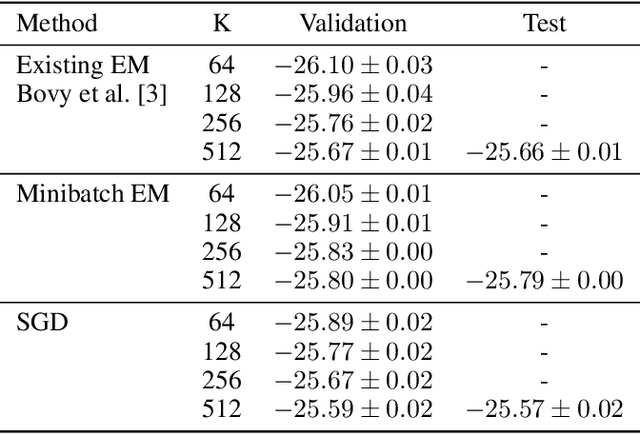
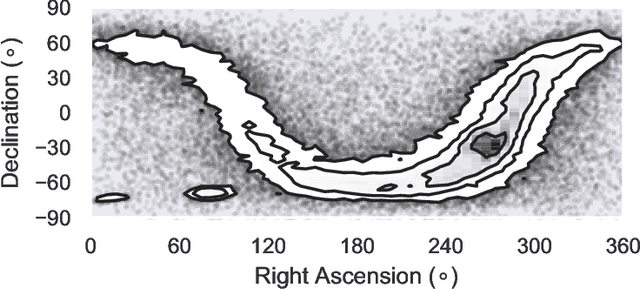
The Extreme Deconvolution method fits a probability density to a dataset where each observation has Gaussian noise added with a known sample-specific covariance, originally intended for use with astronomical datasets. The existing fitting method is batch EM, which would not normally be applied to large datasets such as the Gaia catalog containing noisy observations of a billion stars. We propose two minibatch variants of extreme deconvolution, based on an online variation of the EM algorithm, and direct gradient-based optimisation of the log-likelihood, both of which can run on GPUs. We demonstrate that these methods provide faster fitting, whilst being able to scale to much larger models for use with larger datasets.

CloudLSTM: A Recurrent Neural Model for Spatiotemporal Point-cloud Stream Forecasting

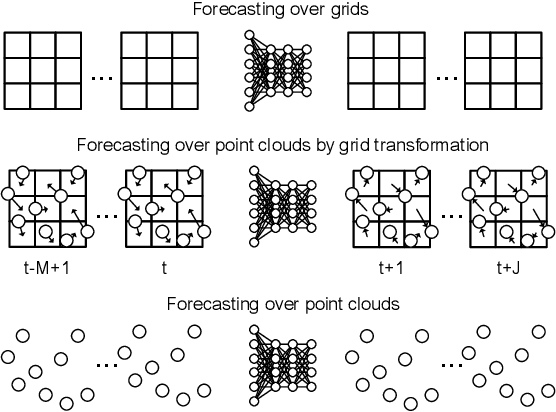
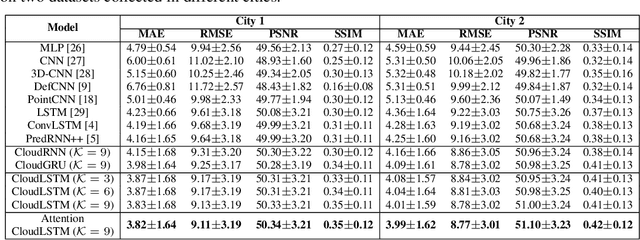
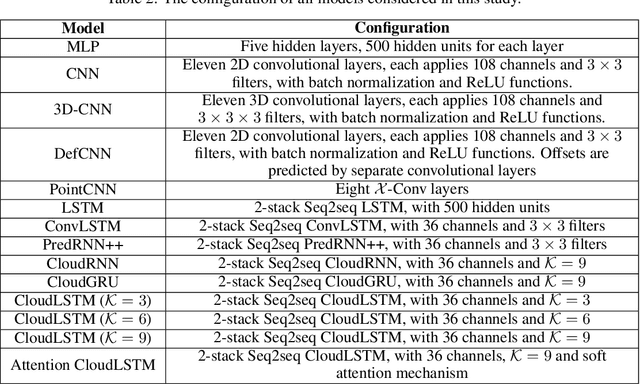
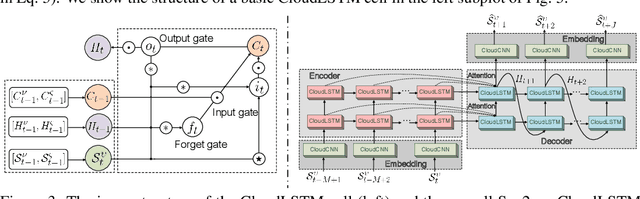
This paper introduces CloudLSTM, a new branch of recurrent neural network models tailored to forecasting over data streams generated by geospatial point-cloud sources. We design a Dynamic Convolution (D-Conv) operator as the core component of CloudLSTMs, which allows performing convolution operations directly over point-clouds and extracts local spatial features from sets of neighboring points that surround different elements of the input. This maintains the permutation invariance of sequence-to-sequence learning frameworks, while enabling learnable neighboring correlations at each time step -- an important aspect in spatiotemporal predictive learning. The D-Conv operator resolves the grid-structural data requirements of existing spatiotemporal forecasting models (e.g. ConvLSTM) and can be easily plugged into traditional LSTM architectures with sequence-to-sequence learning and attention mechanisms. As a case study, we perform antenna-level forecasting of the data traffic generated by mobile services, demonstrating that the proposed CloudLSTM achieves state-of-the-art performance with measurement datasets collected in operational metropolitan-scale mobile network deployments.

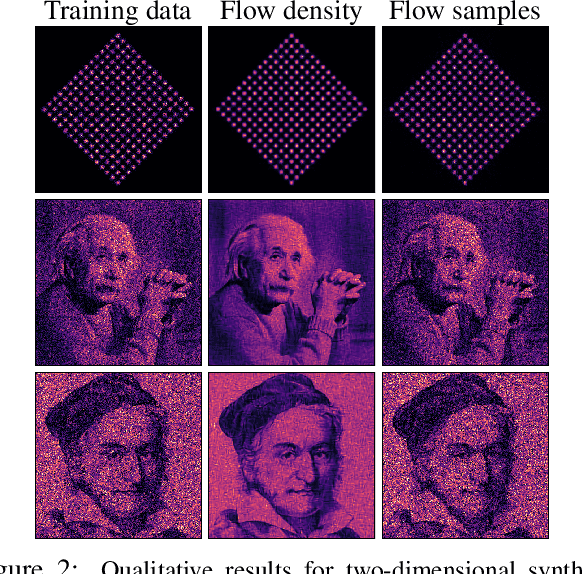
Neural Spline Flows

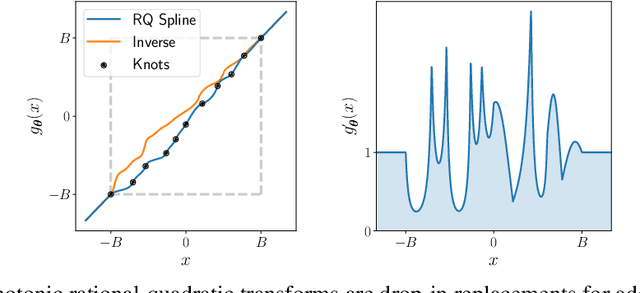
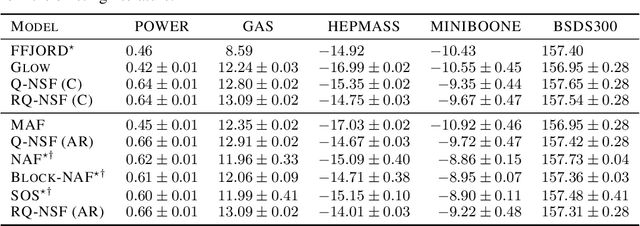
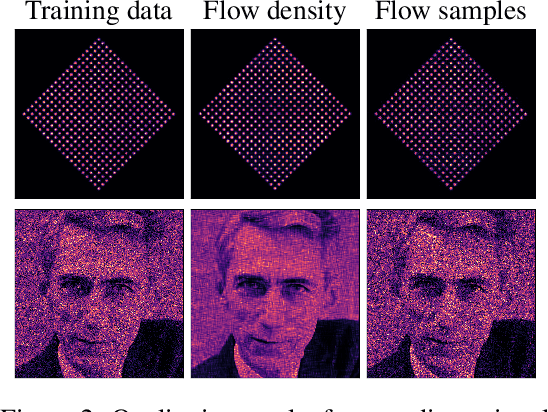
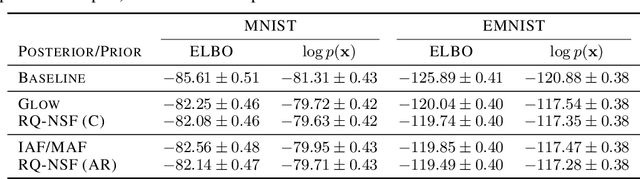
A normalizing flow models a complex probability density as an invertible transformation of a simple base density. Flows based on either coupling or autoregressive transforms both offer exact density evaluation and sampling, but rely on the parameterization of an easily invertible elementwise transformation, whose choice determines the flexibility of these models. Building upon recent work, we propose a fully-differentiable module based on monotonic rational-quadratic splines, which enhances the flexibility of both coupling and autoregressive transforms while retaining analytic invertibility. We demonstrate that neural spline flows improve density estimation, variational inference, and generative modeling of images.

Cubic-Spline Flows

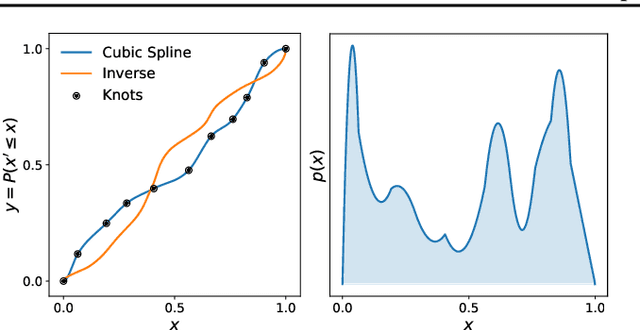
A normalizing flow models a complex probability density as an invertible transformation of a simple density. The invertibility means that we can evaluate densities and generate samples from a flow. In practice, autoregressive flow-based models are slow to invert, making either density estimation or sample generation slow. Flows based on coupling transforms are fast for both tasks, but have previously performed less well at density estimation than autoregressive flows. We stack a new coupling transform, based on monotonic cubic splines, with LU-decomposed linear layers. The resulting cubic-spline flow retains an exact one-pass inverse, can be used to generate high-quality images, and closes the gap with autoregressive flows on a suite of density-estimation tasks.

Dynamic Evaluation of Transformer Language Models

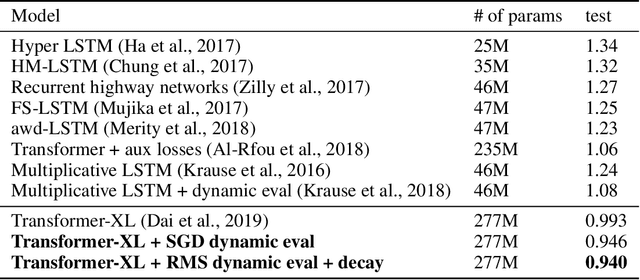
This research note combines two methods that have recently improved the state of the art in language modeling: Transformers and dynamic evaluation. Transformers use stacked layers of self-attention that allow them to capture long range dependencies in sequential data. Dynamic evaluation fits models to the recent sequence history, allowing them to assign higher probabilities to re-occurring sequential patterns. By applying dynamic evaluation to Transformer-XL models, we improve the state of the art on enwik8 from 0.99 to 0.94 bits/char, text8 from 1.08 to 1.04 bits/char, and WikiText-103 from 18.3 to 16.4 perplexity points.