On Contrastive Learning for Likelihood-free Inference
Paper and Code
Feb 10, 2020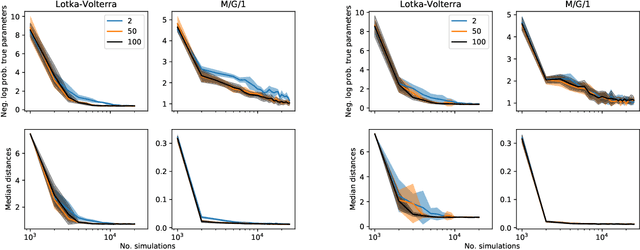
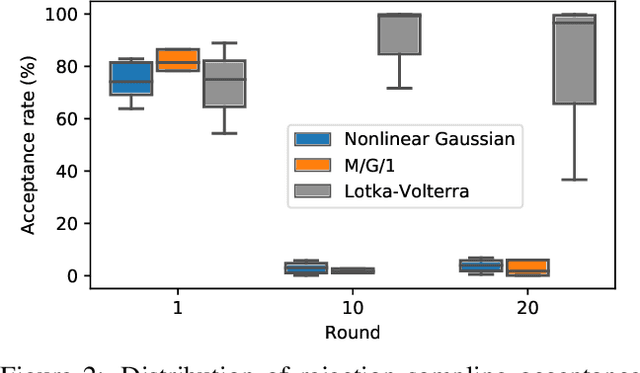
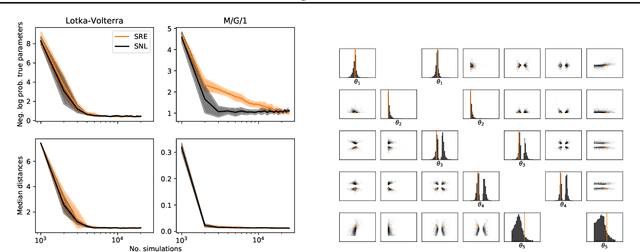
Likelihood-free methods perform parameter inference in stochastic simulator models where evaluating the likelihood is intractable but sampling synthetic data is possible. One class of methods for this likelihood-free problem uses a classifier to distinguish between pairs of parameter-observation samples generated using the simulator and pairs sampled from some reference distribution, which implicitly learns a density ratio proportional to the likelihood. Another popular class of methods fits a conditional distribution to the parameter posterior directly, and a particular recent variant allows for the use of flexible neural density estimators for this task. In this work, we show that both of these approaches can be unified under a general contrastive learning scheme, and clarify how they should be run and compared.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge