Ordering Dimensions with Nested Dropout Normalizing Flows
Paper and Code
Jun 15, 2020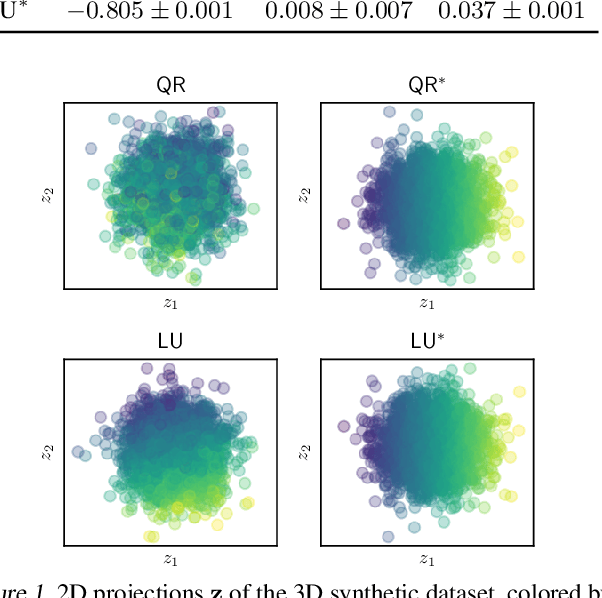
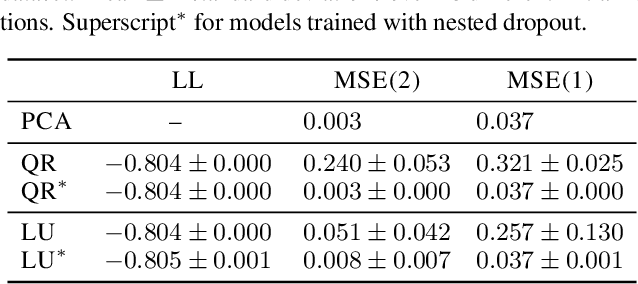

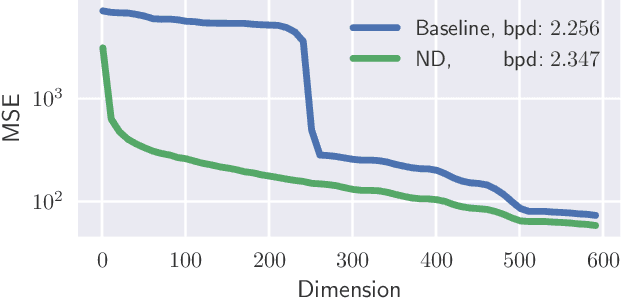
The latent space of normalizing flows must be of the same dimensionality as their output space. This constraint presents a problem if we want to learn low-dimensional, semantically meaningful representations. Recent work has provided compact representations by fitting flows constrained to manifolds, but hasn't defined a density off that manifold. In this work we consider flows with full support in data space, but with ordered latent variables. Like in PCA, the leading latent dimensions define a sequence of manifolds that lie close to the data. We note a trade-off between the flow likelihood and the quality of the ordering, depending on the parameterization of the flow.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge