James A. Ritchie
Density Deconvolution with Normalizing Flows
Jul 13, 2020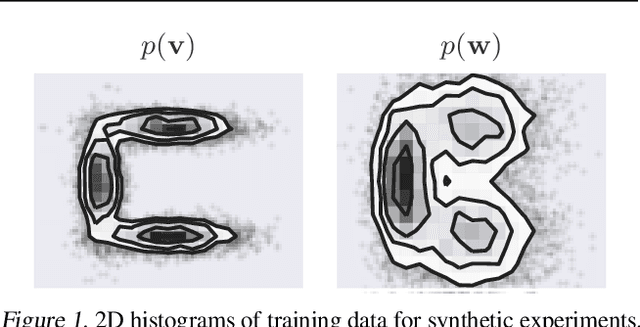
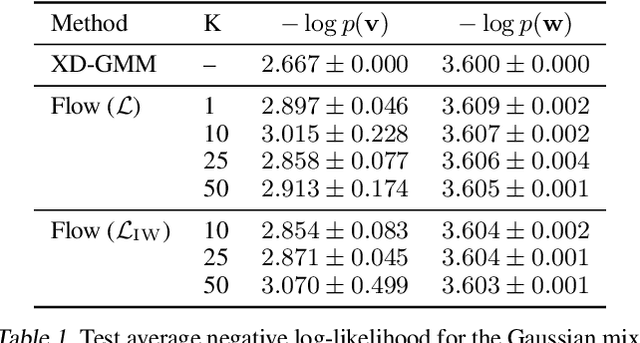
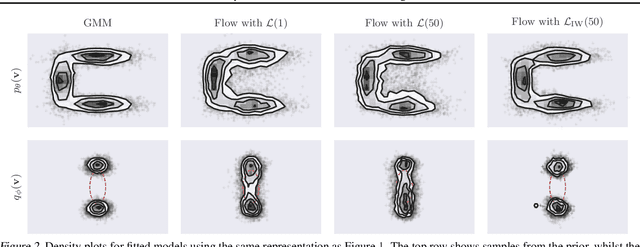
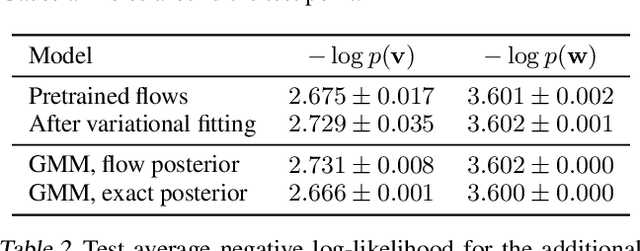
Abstract:Density deconvolution is the task of estimating a probability density function given only noise-corrupted samples. We can fit a Gaussian mixture model to the underlying density by maximum likelihood if the noise is normally distributed, but would like to exploit the superior density estimation performance of normalizing flows and allow for arbitrary noise distributions. Since both adjustments lead to an intractable likelihood, we resort to amortized variational inference. We demonstrate some problems involved in this approach, however, experiments on real data demonstrate that flows can already out-perform Gaussian mixtures for density deconvolution.
Scalable Extreme Deconvolution
Nov 26, 2019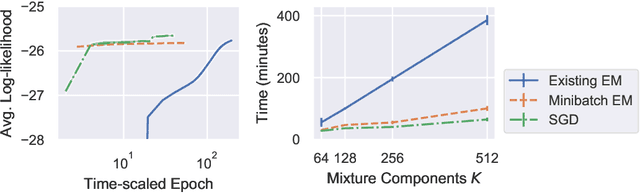
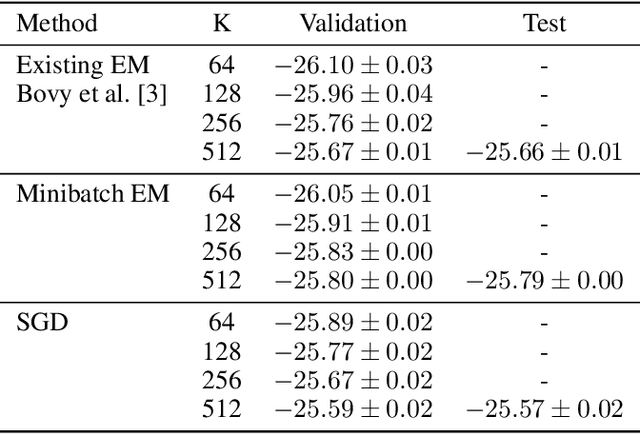
Abstract:The Extreme Deconvolution method fits a probability density to a dataset where each observation has Gaussian noise added with a known sample-specific covariance, originally intended for use with astronomical datasets. The existing fitting method is batch EM, which would not normally be applied to large datasets such as the Gaia catalog containing noisy observations of a billion stars. We propose two minibatch variants of extreme deconvolution, based on an online variation of the EM algorithm, and direct gradient-based optimisation of the log-likelihood, both of which can run on GPUs. We demonstrate that these methods provide faster fitting, whilst being able to scale to much larger models for use with larger datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge