Compressing Multisets with Large Alphabets
Paper and Code
Jul 15, 2021
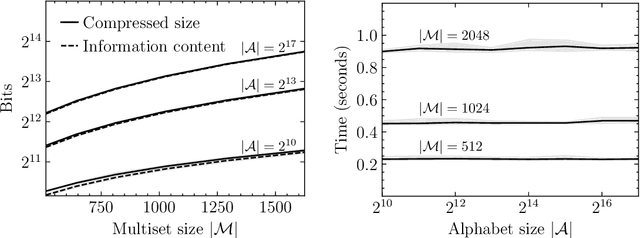
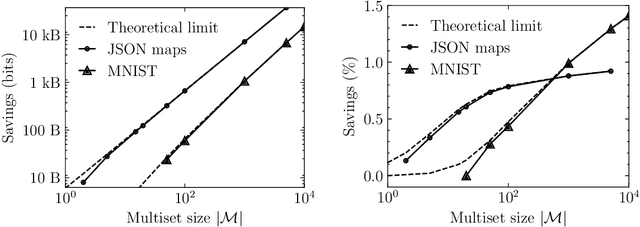
Current methods that optimally compress multisets are not suitable for high-dimensional symbols, as their compute time scales linearly with alphabet size. Compressing a multiset as an ordered sequence with off-the-shelf codecs is computationally more efficient, but has a sub-optimal compression rate, as bits are wasted encoding the order between symbols. We present a method that can recover those bits, assuming symbols are i.i.d., at the cost of an additional $\mathcal{O}(|\mathcal{M}|\log M)$ in average time complexity, where $|\mathcal{M}|$ and $M$ are the total and unique number of symbols in the multiset. Our method is compatible with any prefix-free code. Experiments show that, when paired with efficient coders, our method can efficiently compress high-dimensional sources such as multisets of images and collections of JSON files.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge