Rate-Distortion-Perception Tradeoff Based on the Conditional-Distribution Perception Measure

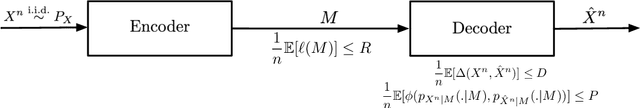
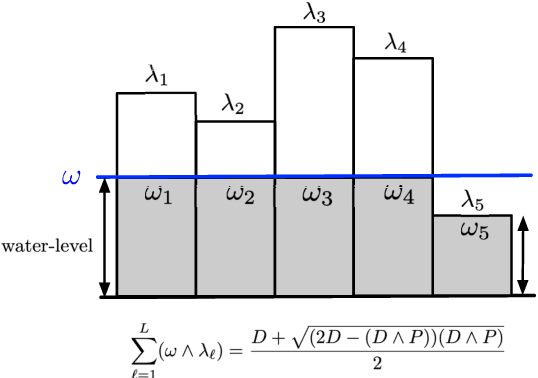
We study the rate-distortion-perception (RDP) tradeoff for a memoryless source model in the asymptotic limit of large block-lengths. Our perception measure is based on a divergence between the distributions of the source and reconstruction sequences conditioned on the encoder output, which was first proposed in [1], [2]. We consider the case when there is no shared randomness between the encoder and the decoder. For the case of discrete memoryless sources we derive a single-letter characterization of the RDP function, thus settling a problem that remains open for the marginal metric introduced in Blau and Michaeli [3] (with no shared randomness). Our achievability scheme is based on lossy source coding with a posterior reference map proposed in [4]. For the case of continuous valued sources under squared error distortion measure and squared quadratic Wasserstein perception measure we also derive a single-letter characterization and show that a noise-adding mechanism at the decoder suffices to achieve the optimal representation. For the case of zero perception loss, we show that our characterization interestingly coincides with the results for the marginal metric derived in [5], [6] and again demonstrate that zero perception loss can be achieved with a $3$-dB penalty in the minimum distortion. Finally we specialize our results to the case of Gaussian sources. We derive the RDP function for vector Gaussian sources and propose a waterfilling type solution. We also partially characterize the RDP function for a mixture of vector Gaussians.

On the Choice of Perception Loss Function for Learned Video Compression

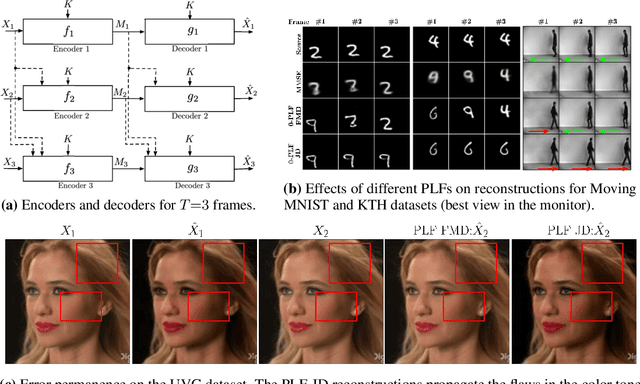
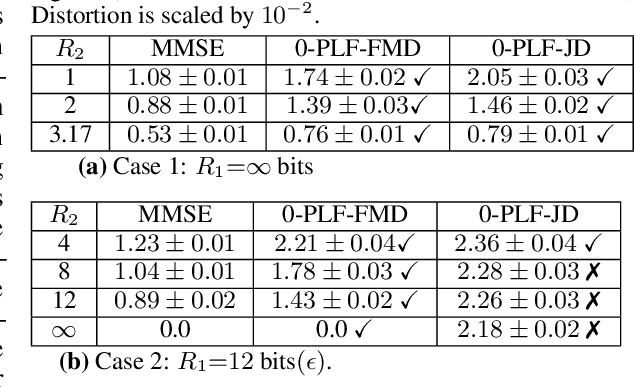
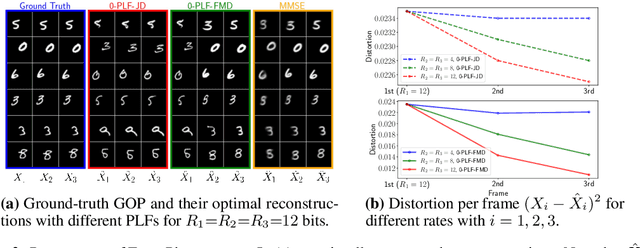
We study causal, low-latency, sequential video compression when the output is subjected to both a mean squared-error (MSE) distortion loss as well as a perception loss to target realism. Motivated by prior approaches, we consider two different perception loss functions (PLFs). The first, PLF-JD, considers the joint distribution (JD) of all the video frames up to the current one, while the second metric, PLF-FMD, considers the framewise marginal distributions (FMD) between the source and reconstruction. Using information theoretic analysis and deep-learning based experiments, we demonstrate that the choice of PLF can have a significant effect on the reconstruction, especially at low-bit rates. In particular, while the reconstruction based on PLF-JD can better preserve the temporal correlation across frames, it also imposes a significant penalty in distortion compared to PLF-FMD and further makes it more difficult to recover from errors made in the earlier output frames. Although the choice of PLF decisively affects reconstruction quality, we also demonstrate that it may not be essential to commit to a particular PLF during encoding and the choice of PLF can be delegated to the decoder. In particular, encoded representations generated by training a system to minimize the MSE (without requiring either PLF) can be {\em near universal} and can generate close to optimal reconstructions for either choice of PLF at the decoder. We validate our results using (one-shot) information-theoretic analysis, detailed study of the rate-distortion-perception tradeoff of the Gauss-Markov source model as well as deep-learning based experiments on moving MNIST and KTH datasets.

M22: A Communication-Efficient Algorithm for Federated Learning Inspired by Rate-Distortion

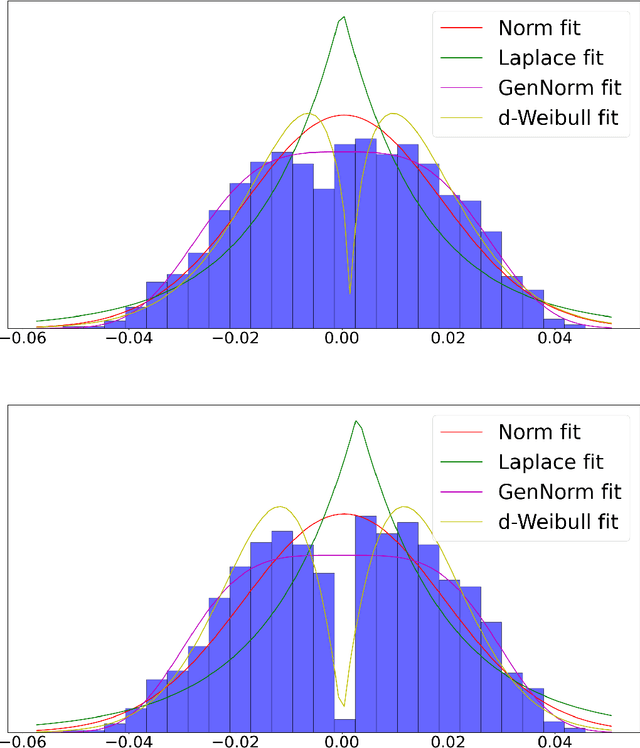
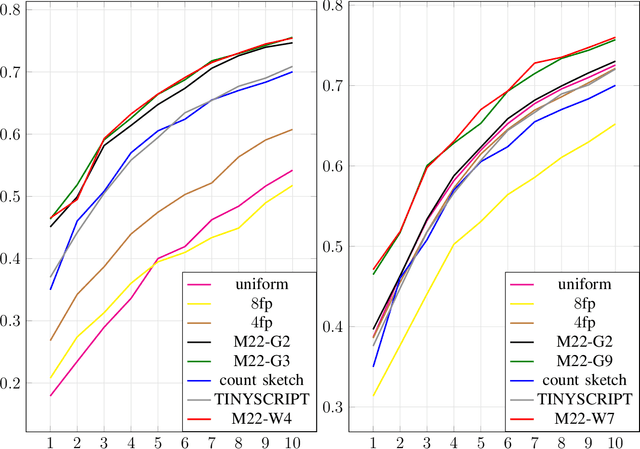
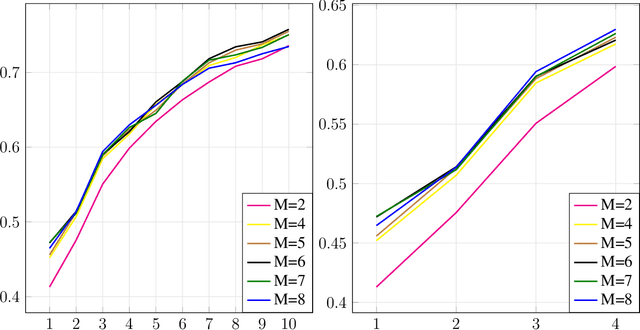
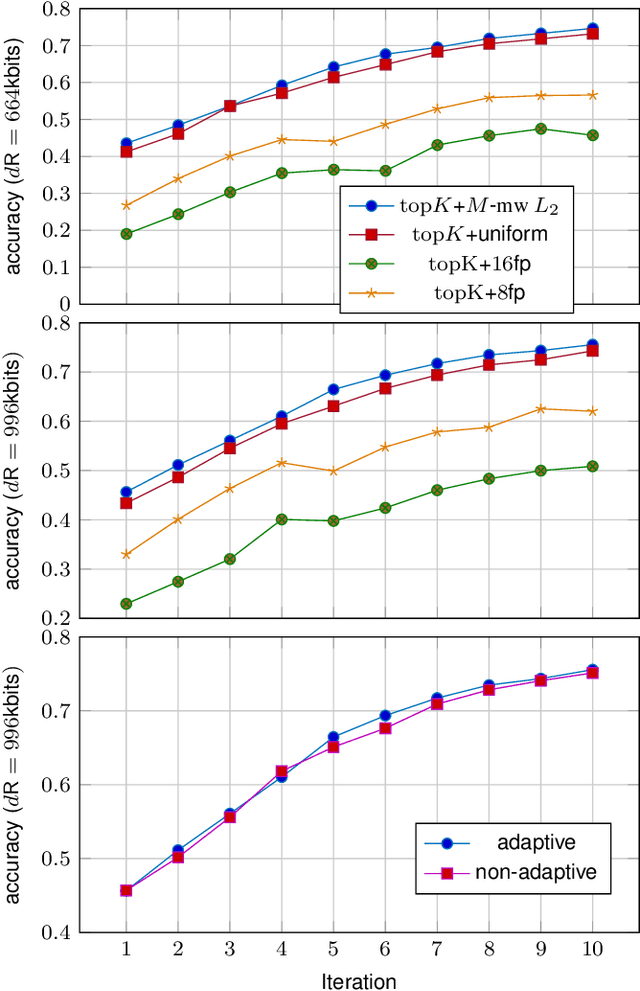
In federated learning (FL), the communication constraint between the remote learners and the Parameter Server (PS) is a crucial bottleneck. For this reason, model updates must be compressed so as to minimize the loss in accuracy resulting from the communication constraint. This paper proposes ``\emph{${\bf M}$-magnitude weighted $L_{\bf 2}$ distortion + $\bf 2$ degrees of freedom''} (M22) algorithm, a rate-distortion inspired approach to gradient compression for federated training of deep neural networks (DNNs). In particular, we propose a family of distortion measures between the original gradient and the reconstruction we referred to as ``$M$-magnitude weighted $L_2$'' distortion, and we assume that gradient updates follow an i.i.d. distribution -- generalized normal or Weibull, which have two degrees of freedom. In both the distortion measure and the gradient, there is one free parameter for each that can be fitted as a function of the iteration number. Given a choice of gradient distribution and distortion measure, we design the quantizer minimizing the expected distortion in gradient reconstruction. To measure the gradient compression performance under a communication constraint, we define the \emph{per-bit accuracy} as the optimal improvement in accuracy that one bit of communication brings to the centralized model over the training period. Using this performance measure, we systematically benchmark the choice of gradient distribution and distortion measure. We provide substantial insights on the role of these choices and argue that significant performance improvements can be attained using such a rate-distortion inspired compressor.

Lossy Gradient Compression: How Much Accuracy Can One Bit Buy?

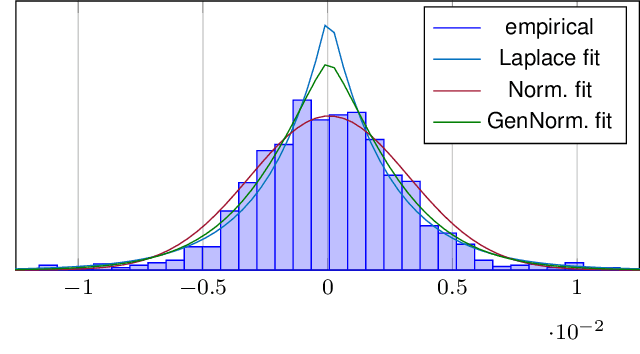
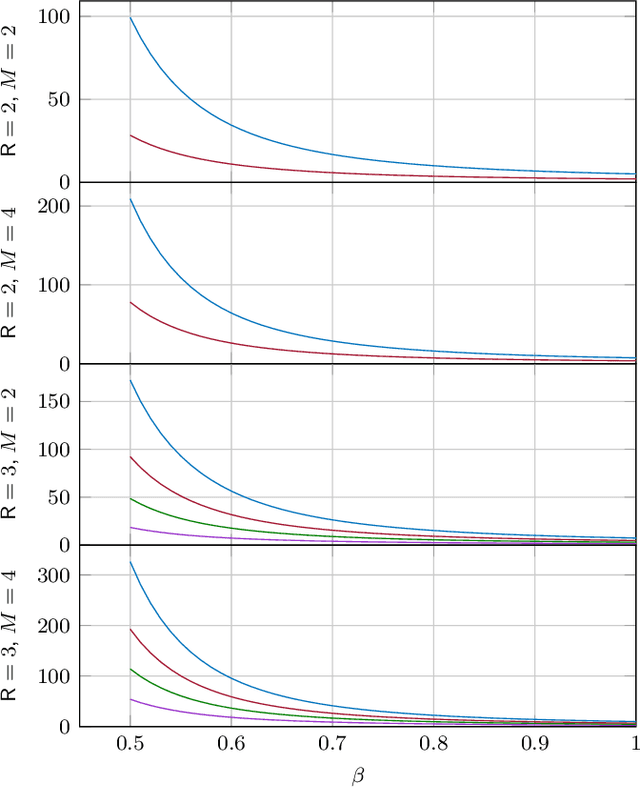
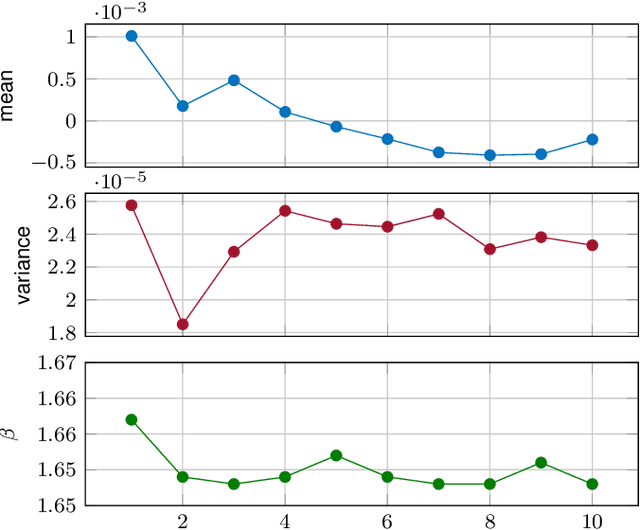
In federated learning (FL), a global model is trained at a Parameter Server (PS) by aggregating model updates obtained from multiple remote learners. Critically, the communication between the remote users and the PS is limited by the available power for transmission, while the transmission from the PS to the remote users can be considered unbounded. This gives rise to the distributed learning scenario in which the updates from the remote learners have to be compressed so as to meet communication rate constraints in the uplink transmission toward the PS. For this problem, one would like to compress the model updates so as to minimize the resulting loss in accuracy. In this paper, we take a rate-distortion approach to answer this question for the distributed training of a deep neural network (DNN). In particular, we define a measure of the compression performance, the \emph{per-bit accuracy}, which addresses the ultimate model accuracy that a bit of communication brings to the centralized model. In order to maximize the per-bit accuracy, we consider modeling the gradient updates at remote learners as a generalized normal distribution. Under this assumption on the model update distribution, we propose a class of distortion measures for the design of quantizer for the compression of the model updates. We argue that this family of distortion measures, which we refer to as "$M$-magnitude weighted $L_2$" norm, capture the practitioner intuition in the choice of gradient compressor. Numerical simulations are provided to validate the proposed approach.