LUMINA: Long-horizon Understanding for Multi-turn Interactive Agents

Large language models can perform well on many isolated tasks, yet they continue to struggle on multi-turn, long-horizon agentic problems that require skills such as planning, state tracking, and long context processing. In this work, we aim to better understand the relative importance of advancing these underlying capabilities for success on such tasks. We develop an oracle counterfactual framework for multi-turn problems that asks: how would an agent perform if it could leverage an oracle to perfectly perform a specific task? The change in the agent's performance due to this oracle assistance allows us to measure the criticality of such oracle skill in the future advancement of AI agents. We introduce a suite of procedurally generated, game-like tasks with tunable complexity. These controlled environments allow us to provide precise oracle interventions, such as perfect planning or flawless state tracking, and make it possible to isolate the contribution of each oracle without confounding effects present in real-world benchmarks. Our results show that while some interventions (e.g., planning) consistently improve performance across settings, the usefulness of other skills is dependent on the properties of the environment and language model. Our work sheds light on the challenges of multi-turn agentic environments to guide the future efforts in the development of AI agents and language models.

Fundamental bounds on efficiency-confidence trade-off for transductive conformal prediction

Transductive conformal prediction addresses the simultaneous prediction for multiple data points. Given a desired confidence level, the objective is to construct a prediction set that includes the true outcomes with the prescribed confidence. We demonstrate a fundamental trade-off between confidence and efficiency in transductive methods, where efficiency is measured by the size of the prediction sets. Specifically, we derive a strict finite-sample bound showing that any non-trivial confidence level leads to exponential growth in prediction set size for data with inherent uncertainty. The exponent scales linearly with the number of samples and is proportional to the conditional entropy of the data. Additionally, the bound includes a second-order term, dispersion, defined as the variance of the log conditional probability distribution. We show that this bound is achievable in an idealized setting. Finally, we examine a special case of transductive prediction where all test data points share the same label. We show that this scenario reduces to the hypothesis testing problem with empirically observed statistics and provide an asymptotically optimal confidence predictor, along with an analysis of the error exponent.

ReQuestNet: A Foundational Learning model for Channel Estimation

In this paper, we present a novel neural architecture for channel estimation (CE) in 5G and beyond, the Recurrent Equivariant UERS Estimation Network (ReQuestNet). It incorporates several practical considerations in wireless communication systems, such as ability to handle variable number of resource block (RB), dynamic number of transmit layers, physical resource block groups (PRGs) bundling size (BS), demodulation reference signal (DMRS) patterns with a single unified model, thereby, drastically simplifying the CE pipeline. Besides it addresses several limitations of the legacy linear MMSE solutions, for example, by being independent of other reference signals and particularly by jointly processing MIMO layers and differently precoded channels with unknown precoding at the receiver. ReQuestNet comprises of two sub-units, CoarseNet followed by RefinementNet. CoarseNet performs per PRG, per transmit-receive (Tx-Rx) stream channel estimation, while RefinementNet refines the CoarseNet channel estimate by incorporating correlations across differently precoded PRGs, and correlation across multiple input multiple output (MIMO) channel spatial dimensions (cross-MIMO). Simulation results demonstrate that ReQuestNet significantly outperforms genie minimum mean squared error (MMSE) CE across a wide range of channel conditions, delay-Doppler profiles, achieving up to 10dB gain at high SNRs. Notably, ReQuestNet generalizes effectively to unseen channel profiles, efficiently exploiting inter-PRG and cross-MIMO correlations under dynamic PRG BS and varying transmit layer allocations.

Local Look-Ahead Guidance via Verifier-in-the-Loop for Automated Theorem Proving

The most promising recent methods for AI reasoning require applying variants of reinforcement learning (RL) either on rolled out trajectories from the model, even for the step-wise rewards, or large quantities of human annotated trajectory data. The reliance on the rolled-out trajectory renders the compute cost and time prohibitively high. In particular, the correctness of a reasoning trajectory can typically only be judged at its completion, leading to sparse rewards in RL or requiring expensive synthetic data generation in expert iteration-like methods. In this work, we focus on the Automatic Theorem Proving (ATP) task and propose a novel verifier-in-the-loop design, which unlike existing approaches that leverage feedback on the entire reasoning trajectory, employs an automated verifier to give intermediate feedback at each step of the reasoning process. Using Lean as the verifier, we empirically show that the step-by-step local verification produces a global improvement in the model's reasoning accuracy and efficiency.

On the Sample Complexity of One Hidden Layer Networks with Equivariance, Locality and Weight Sharing

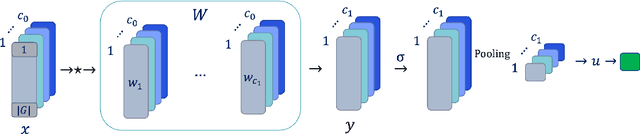
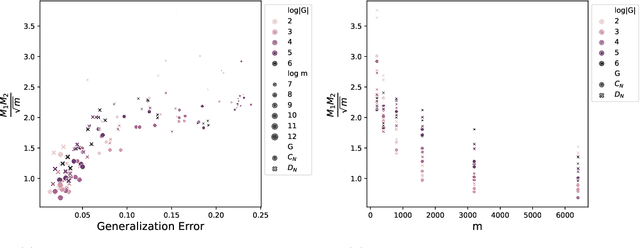
Weight sharing, equivariance, and local filters, as in convolutional neural networks, are believed to contribute to the sample efficiency of neural networks. However, it is not clear how each one of these design choices contribute to the generalization error. Through the lens of statistical learning theory, we aim to provide an insight into this question by characterizing the relative impact of each choice on the sample complexity. We obtain lower and upper sample complexity bounds for a class of single hidden layer networks. It is shown that the gain of equivariance is directly manifested in the bound, while getting a similar increase for weight sharing depends on the sharing mechanism. Among our results, we obtain a completely dimension-free bound for equivariant networks for a class of pooling operations. We show that the bound depends merely on the norm of filters, which is tighter than using the spectral norm of the respective matrix. We also characterize the trade-off in sample complexity between the parametrization of filters in spatial and frequency domains, particularly when spatial filters are localized as in vanilla convolutional neural networks.

Multi-Draft Speculative Sampling: Canonical Architectures and Theoretical Limits

We consider multi-draft speculative sampling, where the proposal sequences are sampled independently from different draft models. At each step, a token-level draft selection scheme takes a list of valid tokens as input and produces an output token whose distribution matches that of the target model. Previous works have demonstrated that the optimal scheme (which maximizes the probability of accepting one of the input tokens) can be cast as a solution to a linear program. In this work we show that the optimal scheme can be decomposed into a two-step solution: in the first step an importance sampling (IS) type scheme is used to select one intermediate token; in the second step (single-draft) speculative sampling is applied to generate the output token. For the case of two identical draft models we further 1) establish a necessary and sufficient condition on the distributions of the target and draft models for the acceptance probability to equal one and 2) provide an explicit expression for the optimal acceptance probability. Our theoretical analysis also motives a new class of token-level selection scheme based on weighted importance sampling. Our experimental results demonstrate consistent improvements in the achievable block efficiency and token rates over baseline schemes in a number of scenarios.

Reinforcement Learning of Adaptive Acquisition Policies for Inverse Problems

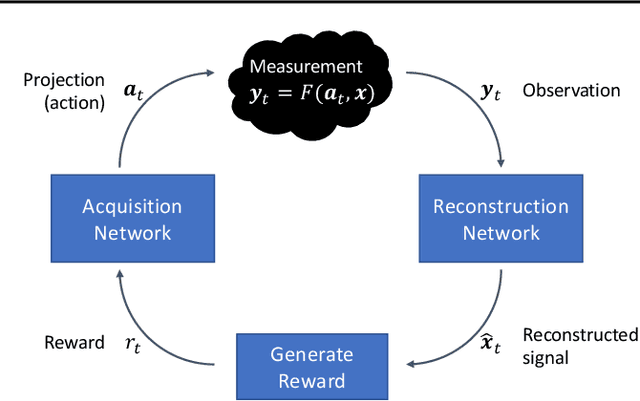
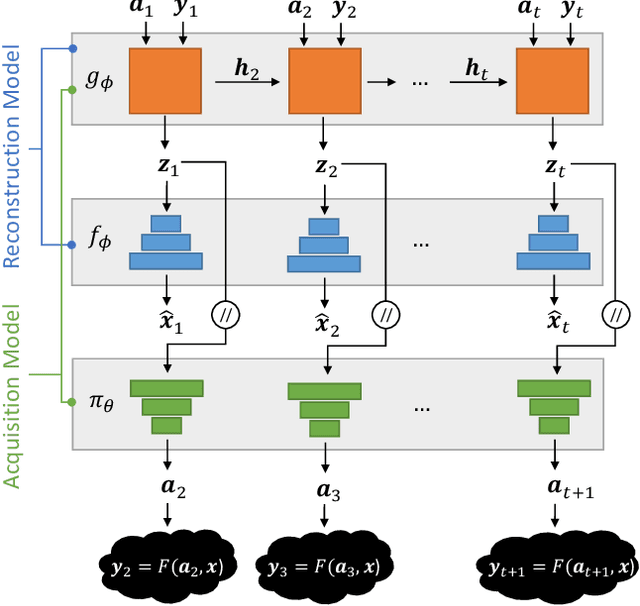
A promising way to mitigate the expensive process of obtaining a high-dimensional signal is to acquire a limited number of low-dimensional measurements and solve an under-determined inverse problem by utilizing the structural prior about the signal. In this paper, we focus on adaptive acquisition schemes to save further the number of measurements. To this end, we propose a reinforcement learning-based approach that sequentially collects measurements to better recover the underlying signal by acquiring fewer measurements. Our approach applies to general inverse problems with continuous action spaces and jointly learns the recovery algorithm. Using insights obtained from theoretical analysis, we also provide a probabilistic design for our methods using variational formulation. We evaluate our approach on multiple datasets and with two measurement spaces (Gaussian, Radon). Our results confirm the benefits of adaptive strategies in low-acquisition horizon settings.

Variational Learning ISTA

Compressed sensing combines the power of convex optimization techniques with a sparsity-inducing prior on the signal space to solve an underdetermined system of equations. For many problems, the sparsifying dictionary is not directly given, nor its existence can be assumed. Besides, the sensing matrix can change across different scenarios. Addressing these issues requires solving a sparse representation learning problem, namely dictionary learning, taking into account the epistemic uncertainty of the learned dictionaries and, finally, jointly learning sparse representations and reconstructions under varying sensing matrix conditions. We address both concerns by proposing a variant of the LISTA architecture. First, we introduce Augmented Dictionary Learning ISTA (A-DLISTA), which incorporates an augmentation module to adapt parameters to the current measurement setup. Then, we propose to learn a distribution over dictionaries via a variational approach, dubbed Variational Learning ISTA (VLISTA). VLISTA exploits A-DLISTA as the likelihood model and approximates a posterior distribution over the dictionaries as part of an unfolded LISTA-based recovery algorithm. As a result, VLISTA provides a probabilistic way to jointly learn the dictionary distribution and the reconstruction algorithm with varying sensing matrices. We provide theoretical and experimental support for our architecture and show that our model learns calibrated uncertainties.

Probabilistic and Differentiable Wireless Simulation with Geometric Transformers

Modelling the propagation of electromagnetic signals is critical for designing modern communication systems. While there are precise simulators based on ray tracing, they do not lend themselves to solving inverse problems or the integration in an automated design loop. We propose to address these challenges through differentiable neural surrogates that exploit the geometric aspects of the problem. We first introduce the Wireless Geometric Algebra Transformer (Wi-GATr), a generic backbone architecture for simulating wireless propagation in a 3D environment. It uses versatile representations based on geometric algebra and is equivariant with respect to E(3), the symmetry group of the underlying physics. Second, we study two algorithmic approaches to signal prediction and inverse problems based on differentiable predictive modelling and diffusion models. We show how these let us predict received power, localize receivers, and reconstruct the 3D environment from the received signal. Finally, we introduce two large, geometry-focused datasets of wireless signal propagation in indoor scenes. In experiments, we show that our geometry-forward approach achieves higher-fidelity predictions with less data than various baselines.

Simulating, Fast and Slow: Learning Policies for Black-Box Optimization

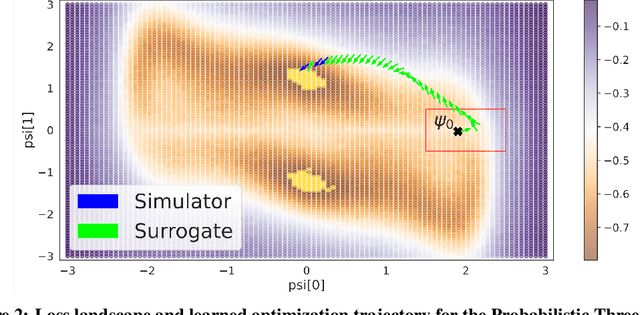
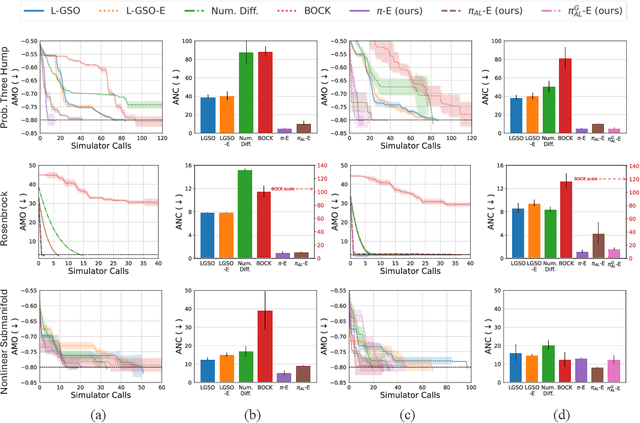
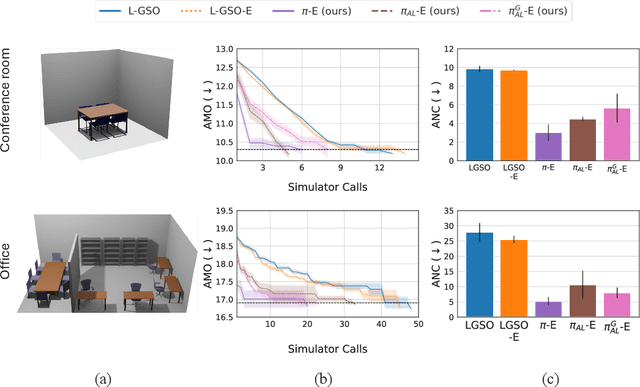
In recent years, solving optimization problems involving black-box simulators has become a point of focus for the machine learning community due to their ubiquity in science and engineering. The simulators describe a forward process $f_{\mathrm{sim}}: (\psi, x) \rightarrow y$ from simulation parameters $\psi$ and input data $x$ to observations $y$, and the goal of the optimization problem is to find parameters $\psi$ that minimize a desired loss function. Sophisticated optimization algorithms typically require gradient information regarding the forward process, $f_{\mathrm{sim}}$, with respect to the parameters $\psi$. However, obtaining gradients from black-box simulators can often be prohibitively expensive or, in some cases, impossible. Furthermore, in many applications, practitioners aim to solve a set of related problems. Thus, starting the optimization ``ab initio", i.e. from scratch, each time might be inefficient if the forward model is expensive to evaluate. To address those challenges, this paper introduces a novel method for solving classes of similar black-box optimization problems by learning an active learning policy that guides a differentiable surrogate's training and uses the surrogate's gradients to optimize the simulation parameters with gradient descent. After training the policy, downstream optimization of problems involving black-box simulators requires up to $\sim$90\% fewer expensive simulator calls compared to baselines such as local surrogate-based approaches, numerical optimization, and Bayesian methods.