ReQuestNet: A Foundational Learning model for Channel Estimation

In this paper, we present a novel neural architecture for channel estimation (CE) in 5G and beyond, the Recurrent Equivariant UERS Estimation Network (ReQuestNet). It incorporates several practical considerations in wireless communication systems, such as ability to handle variable number of resource block (RB), dynamic number of transmit layers, physical resource block groups (PRGs) bundling size (BS), demodulation reference signal (DMRS) patterns with a single unified model, thereby, drastically simplifying the CE pipeline. Besides it addresses several limitations of the legacy linear MMSE solutions, for example, by being independent of other reference signals and particularly by jointly processing MIMO layers and differently precoded channels with unknown precoding at the receiver. ReQuestNet comprises of two sub-units, CoarseNet followed by RefinementNet. CoarseNet performs per PRG, per transmit-receive (Tx-Rx) stream channel estimation, while RefinementNet refines the CoarseNet channel estimate by incorporating correlations across differently precoded PRGs, and correlation across multiple input multiple output (MIMO) channel spatial dimensions (cross-MIMO). Simulation results demonstrate that ReQuestNet significantly outperforms genie minimum mean squared error (MMSE) CE across a wide range of channel conditions, delay-Doppler profiles, achieving up to 10dB gain at high SNRs. Notably, ReQuestNet generalizes effectively to unseen channel profiles, efficiently exploiting inter-PRG and cross-MIMO correlations under dynamic PRG BS and varying transmit layer allocations.

Local Look-Ahead Guidance via Verifier-in-the-Loop for Automated Theorem Proving

The most promising recent methods for AI reasoning require applying variants of reinforcement learning (RL) either on rolled out trajectories from the model, even for the step-wise rewards, or large quantities of human annotated trajectory data. The reliance on the rolled-out trajectory renders the compute cost and time prohibitively high. In particular, the correctness of a reasoning trajectory can typically only be judged at its completion, leading to sparse rewards in RL or requiring expensive synthetic data generation in expert iteration-like methods. In this work, we focus on the Automatic Theorem Proving (ATP) task and propose a novel verifier-in-the-loop design, which unlike existing approaches that leverage feedback on the entire reasoning trajectory, employs an automated verifier to give intermediate feedback at each step of the reasoning process. Using Lean as the verifier, we empirically show that the step-by-step local verification produces a global improvement in the model's reasoning accuracy and efficiency.

On the Sample Complexity of One Hidden Layer Networks with Equivariance, Locality and Weight Sharing

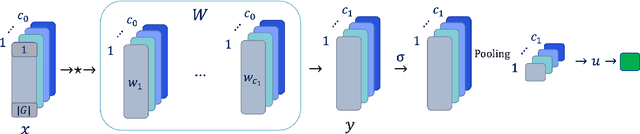
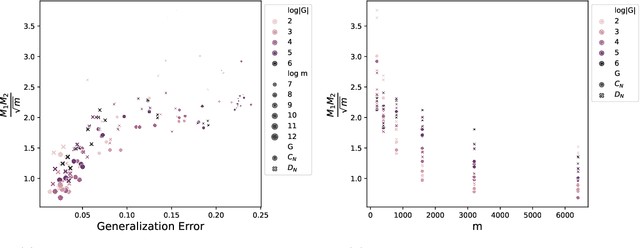
Weight sharing, equivariance, and local filters, as in convolutional neural networks, are believed to contribute to the sample efficiency of neural networks. However, it is not clear how each one of these design choices contribute to the generalization error. Through the lens of statistical learning theory, we aim to provide an insight into this question by characterizing the relative impact of each choice on the sample complexity. We obtain lower and upper sample complexity bounds for a class of single hidden layer networks. It is shown that the gain of equivariance is directly manifested in the bound, while getting a similar increase for weight sharing depends on the sharing mechanism. Among our results, we obtain a completely dimension-free bound for equivariant networks for a class of pooling operations. We show that the bound depends merely on the norm of filters, which is tighter than using the spectral norm of the respective matrix. We also characterize the trade-off in sample complexity between the parametrization of filters in spatial and frequency domains, particularly when spatial filters are localized as in vanilla convolutional neural networks.

Adaptive Sampling for Continuous Group Equivariant Neural Networks

Steerable networks, which process data with intrinsic symmetries, often use Fourier-based nonlinearities that require sampling from the entire group, leading to a need for discretization in continuous groups. As the number of samples increases, both performance and equivariance improve, yet this also leads to higher computational costs. To address this, we introduce an adaptive sampling approach that dynamically adjusts the sampling process to the symmetries in the data, reducing the number of required group samples and lowering the computational demands. We explore various implementations and their effects on model performance, equivariance, and computational efficiency. Our findings demonstrate improved model performance, and a marginal increase in memory efficiency.

A Probabilistic Approach to Learning the Degree of Equivariance in Steerable CNNs

Steerable convolutional neural networks (SCNNs) enhance task performance by modelling geometric symmetries through equivariance constraints on weights. Yet, unknown or varying symmetries can lead to overconstrained weights and decreased performance. To address this, this paper introduces a probabilistic method to learn the degree of equivariance in SCNNs. We parameterise the degree of equivariance as a likelihood distribution over the transformation group using Fourier coefficients, offering the option to model layer-wise and shared equivariance. These likelihood distributions are regularised to ensure an interpretable degree of equivariance across the network. Advantages include the applicability to many types of equivariant networks through the flexible framework of SCNNs and the ability to learn equivariance with respect to any subgroup of any compact group without requiring additional layers. Our experiments reveal competitive performance on datasets with mixed symmetries, with learnt likelihood distributions that are representative of the underlying degree of equivariance.

Equivariant amortized inference of poses for cryo-EM

Cryo-EM is a vital technique for determining 3D structure of biological molecules such as proteins and viruses. The cryo-EM reconstruction problem is challenging due to the high noise levels, the missing poses of particles, and the computational demands of processing large datasets. A promising solution to these challenges lies in the use of amortized inference methods, which have shown particular efficacy in pose estimation for large datasets. However, these methods also encounter convergence issues, often necessitating sophisticated initialization strategies or engineered solutions for effective convergence. Building upon the existing cryoAI pipeline, which employs a symmetric loss function to address convergence problems, this work explores the emergence and persistence of these issues within the pipeline. Additionally, we explore the impact of equivariant amortized inference on enhancing convergence. Our investigations reveal that, when applied to simulated data, a pipeline incorporating an equivariant encoder not only converges faster and more frequently than the standard approach but also demonstrates superior performance in terms of pose estimation accuracy and the resolution of the reconstructed volume. Notably, $D_4$-equivariant encoders make the symmetric loss superfluous and, therefore, allow for a more efficient reconstruction pipeline.

Algebraic Topological Networks via the Persistent Local Homology Sheaf

In this work, we introduce a novel approach based on algebraic topology to enhance graph convolution and attention modules by incorporating local topological properties of the data. To do so, we consider the framework of sheaf neural networks, which has been previously leveraged to incorporate additional structure into graph neural networks' features and construct more expressive, non-isotropic messages. Specifically, given an input simplicial complex (e.g. generated by the cliques of a graph or the neighbors in a point cloud), we construct its local homology sheaf, which assigns to each node the vector space of its local homology. The intermediate features of our networks live in these vector spaces and we leverage the associated sheaf Laplacian to construct more complex linear messages between them. Moreover, we extend this approach by considering the persistent version of local homology associated with a weighted simplicial complex (e.g., built from pairwise distances of nodes embeddings). This i) solves the problem of the lack of a natural choice of basis for the local homology vector spaces and ii) makes the sheaf itself differentiable, which enables our models to directly optimize the topology of their intermediate features.

Neural Lattice Reduction: A Self-Supervised Geometric Deep Learning Approach

Lattice reduction is a combinatorial optimization problem aimed at finding the most orthogonal basis in a given lattice. In this work, we address lattice reduction via deep learning methods. We design a deep neural model outputting factorized unimodular matrices and train it in a self-supervised manner by penalizing non-orthogonal lattice bases. We incorporate the symmetries of lattice reduction into the model by making it invariant and equivariant with respect to appropriate continuous and discrete groups.

Implicit Neural Convolutional Kernels for Steerable CNNs

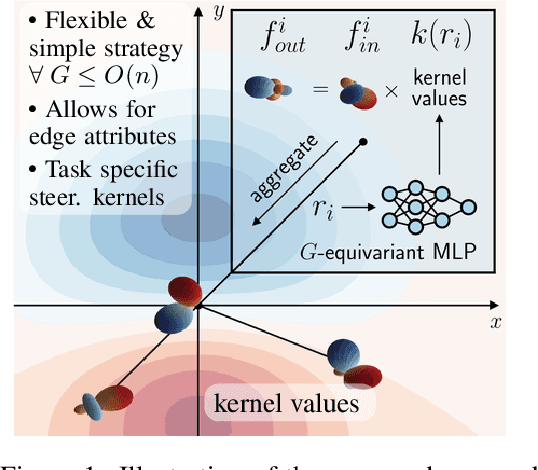
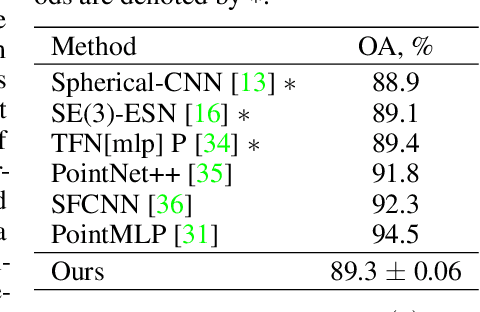
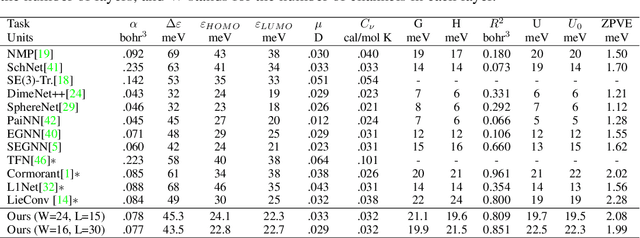
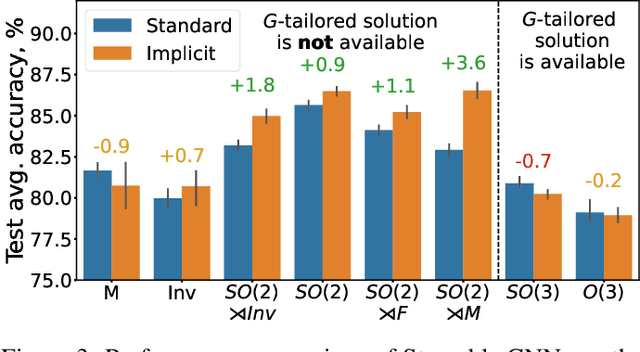
Steerable convolutional neural networks (CNNs) provide a general framework for building neural networks equivariant to translations and other transformations belonging to an origin-preserving group $G$, such as reflections and rotations. They rely on standard convolutions with $G$-steerable kernels obtained by analytically solving the group-specific equivariance constraint imposed onto the kernel space. As the solution is tailored to a particular group $G$, the implementation of a kernel basis does not generalize to other symmetry transformations, which complicates the development of group equivariant models. We propose using implicit neural representation via multi-layer perceptrons (MLPs) to parameterize $G$-steerable kernels. The resulting framework offers a simple and flexible way to implement Steerable CNNs and generalizes to any group $G$ for which a $G$-equivariant MLP can be built. We apply our method to point cloud (ModelNet-40) and molecular data (QM9) and demonstrate a significant improvement in performance compared to standard Steerable CNNs.

A PAC-Bayesian Generalization Bound for Equivariant Networks

Equivariant networks capture the inductive bias about the symmetry of the learning task by building those symmetries into the model. In this paper, we study how equivariance relates to generalization error utilizing PAC Bayesian analysis for equivariant networks, where the transformation laws of feature spaces are determined by group representations. By using perturbation analysis of equivariant networks in Fourier domain for each layer, we derive norm-based PAC-Bayesian generalization bounds. The bound characterizes the impact of group size, and multiplicity and degree of irreducible representations on the generalization error and thereby provide a guideline for selecting them. In general, the bound indicates that using larger group size in the model improves the generalization error substantiated by extensive numerical experiments.