Implicit Neural Convolutional Kernels for Steerable CNNs
Paper and Code
Dec 12, 2022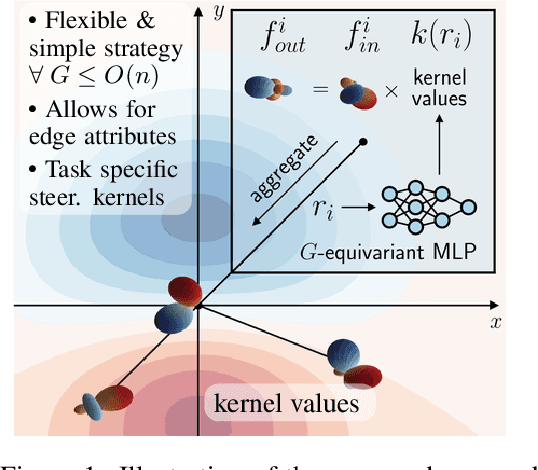
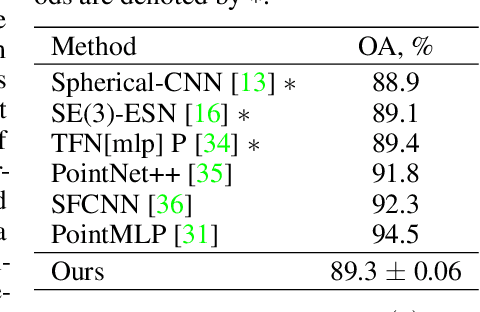
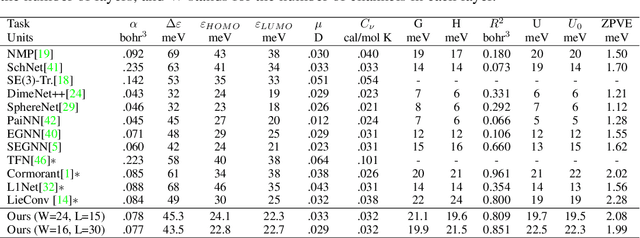
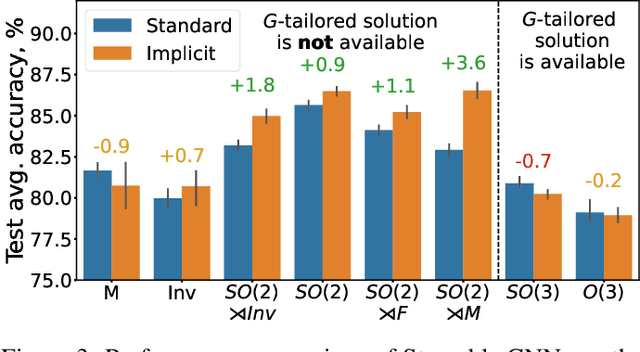
Steerable convolutional neural networks (CNNs) provide a general framework for building neural networks equivariant to translations and other transformations belonging to an origin-preserving group $G$, such as reflections and rotations. They rely on standard convolutions with $G$-steerable kernels obtained by analytically solving the group-specific equivariance constraint imposed onto the kernel space. As the solution is tailored to a particular group $G$, the implementation of a kernel basis does not generalize to other symmetry transformations, which complicates the development of group equivariant models. We propose using implicit neural representation via multi-layer perceptrons (MLPs) to parameterize $G$-steerable kernels. The resulting framework offers a simple and flexible way to implement Steerable CNNs and generalizes to any group $G$ for which a $G$-equivariant MLP can be built. We apply our method to point cloud (ModelNet-40) and molecular data (QM9) and demonstrate a significant improvement in performance compared to standard Steerable CNNs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge