Neural Lattice Reduction: A Self-Supervised Geometric Deep Learning Approach

Lattice reduction is a combinatorial optimization problem aimed at finding the most orthogonal basis in a given lattice. In this work, we address lattice reduction via deep learning methods. We design a deep neural model outputting factorized unimodular matrices and train it in a self-supervised manner by penalizing non-orthogonal lattice bases. We incorporate the symmetries of lattice reduction into the model by making it invariant and equivariant with respect to appropriate continuous and discrete groups.

Equivariant Priors for Compressed Sensing with Unknown Orientation

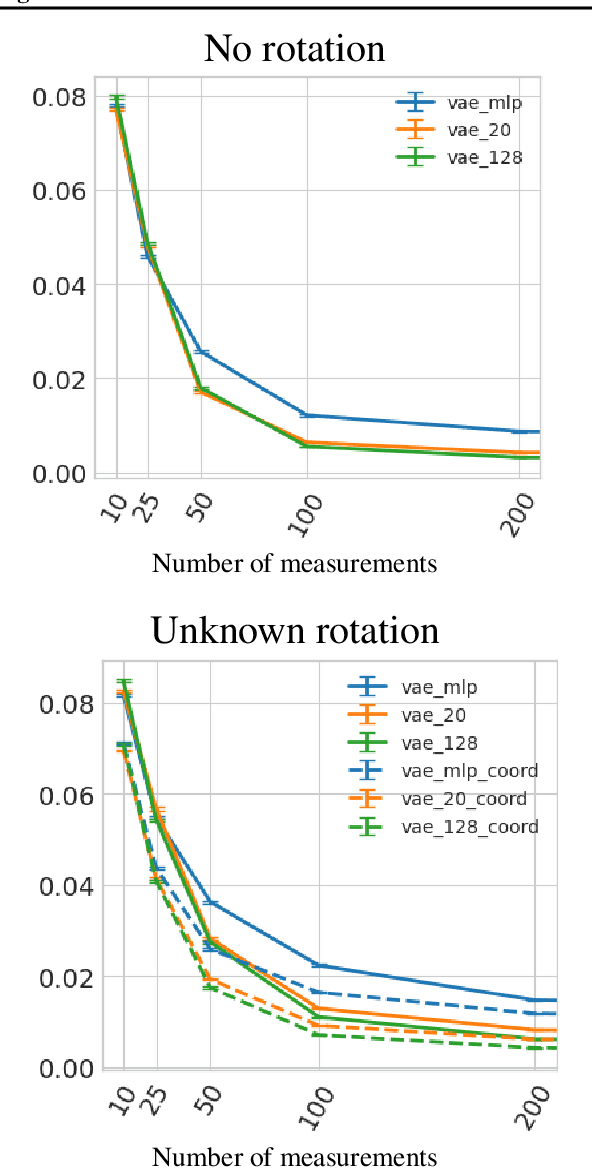
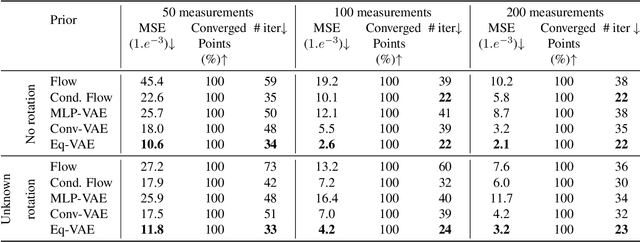
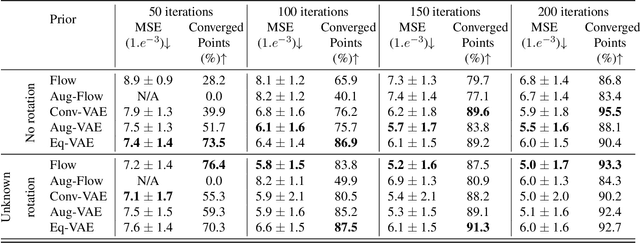
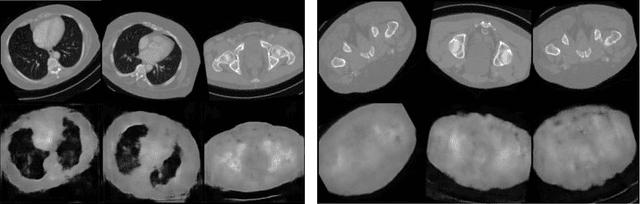
In compressed sensing, the goal is to reconstruct the signal from an underdetermined system of linear measurements. Thus, prior knowledge about the signal of interest and its structure is required. Additionally, in many scenarios, the signal has an unknown orientation prior to measurements. To address such recovery problems, we propose using equivariant generative models as a prior, which encapsulate orientation information in their latent space. Thereby, we show that signals with unknown orientations can be recovered with iterative gradient descent on the latent space of these models and provide additional theoretical recovery guarantees. We construct an equivariant variational autoencoder and use the decoder as generative prior for compressed sensing. We discuss additional potential gains of the proposed approach in terms of convergence and latency.

Neural Augmentation of Kalman Filter with Hypernetwork for Channel Tracking

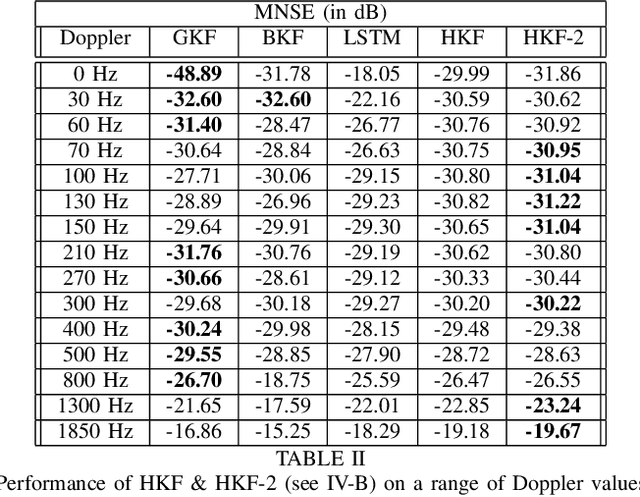
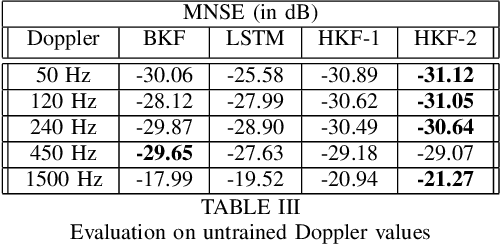
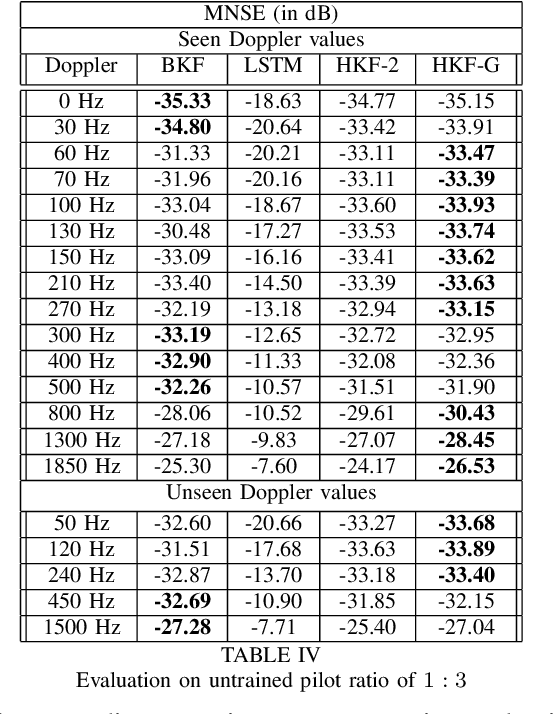
We propose Hypernetwork Kalman Filter (HKF) for tracking applications with multiple different dynamics. The HKF combines generalization power of Kalman filters with expressive power of neural networks. Instead of keeping a bank of Kalman filters and choosing one based on approximating the actual dynamics, HKF adapts itself to each dynamics based on the observed sequence. Through extensive experiments on CDL-B channel model, we show that the HKF can be used for tracking the channel over a wide range of Doppler values, matching Kalman filter performance with genie Doppler information. At high Doppler values, it achieves around 2dB gain over genie Kalman filter. The HKF generalizes well to unseen Doppler, SNR values and pilot patterns unlike LSTM, which suffers from severe performance degradation.

RE-MIMO: Recurrent and Permutation Equivariant Neural MIMO Detection

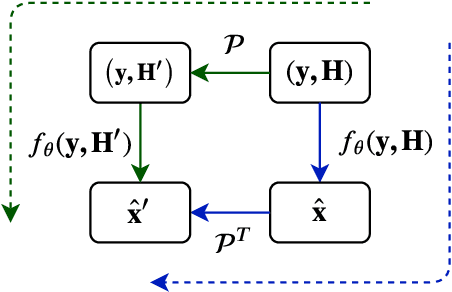
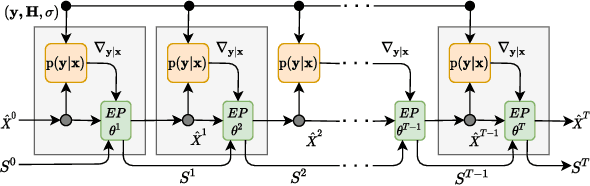
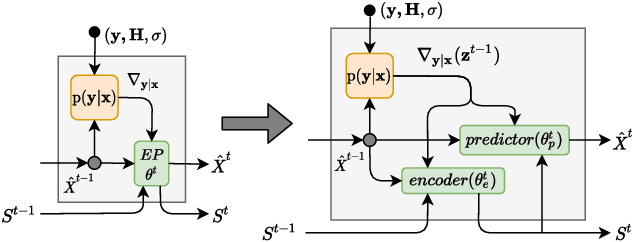
In this paper, we present a novel neural network for MIMO symbol detection. It is motivated by several important considerations in wireless communication systems; permutation equivariance and a variable number of users. The neural detector learns an iterative decoding algorithm that is implemented as a stack of iterative units. Each iterative unit is a neural computation module comprising of 3 sub-modules: the likelihood module, the encoder module, and the predictor module. The likelihood module injects information about the generative (forward) process into the neural network. The encoder-predictor modules together update the state vector and symbol estimates. The encoder module updates the state vector and employs a transformer based attention network to handle the interactions among the users in a permutation equivariant manner. The predictor module refines the symbol estimates. The modular and permutation equivariant architecture allows for dealing with a varying number of users. The resulting neural detector architecture is unique and exhibits several desirable properties unseen in any of the previously proposed neural detectors. We compare its performance against existing methods and the results show the ability of our network to efficiently handle a variable number of transmitters with high accuracy.