Equivariant Priors for Compressed Sensing with Unknown Orientation
Paper and Code
Jun 28, 2022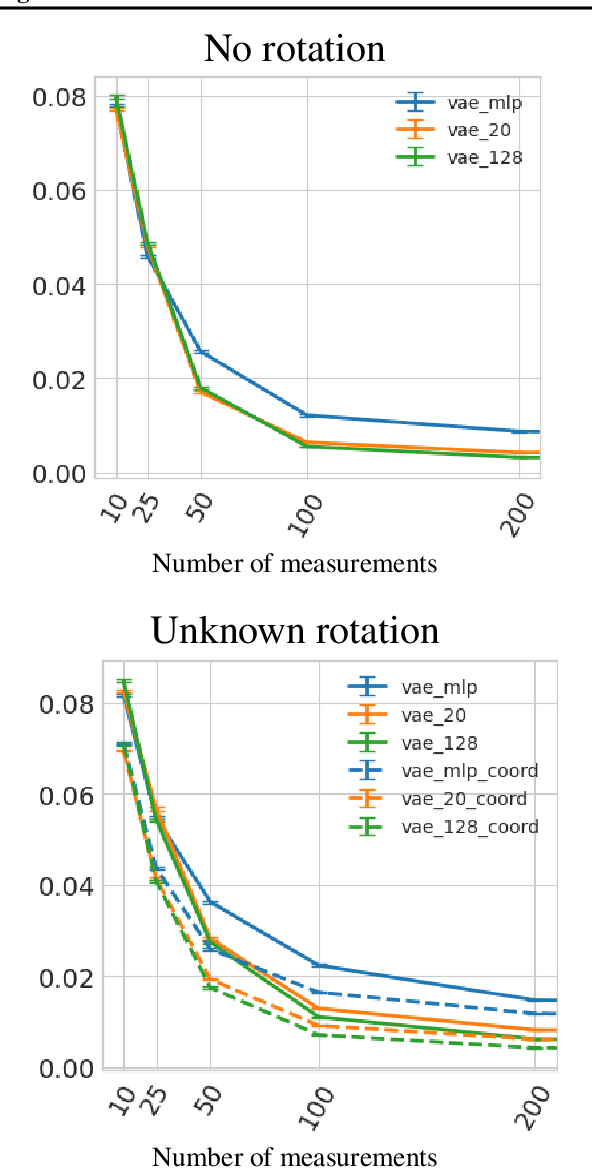
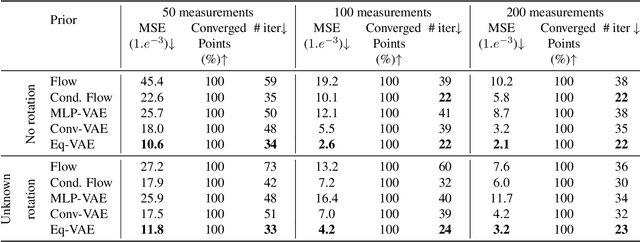
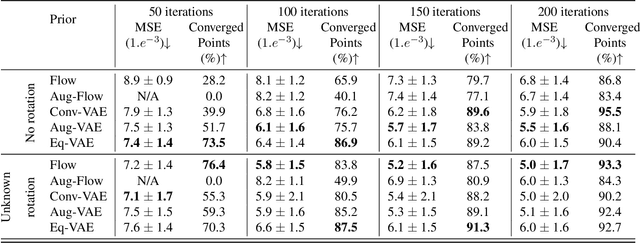
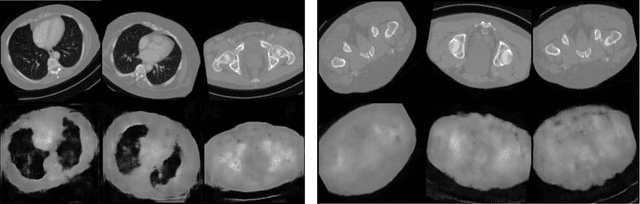
In compressed sensing, the goal is to reconstruct the signal from an underdetermined system of linear measurements. Thus, prior knowledge about the signal of interest and its structure is required. Additionally, in many scenarios, the signal has an unknown orientation prior to measurements. To address such recovery problems, we propose using equivariant generative models as a prior, which encapsulate orientation information in their latent space. Thereby, we show that signals with unknown orientations can be recovered with iterative gradient descent on the latent space of these models and provide additional theoretical recovery guarantees. We construct an equivariant variational autoencoder and use the decoder as generative prior for compressed sensing. We discuss additional potential gains of the proposed approach in terms of convergence and latency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge