Reinforcement Learning of Adaptive Acquisition Policies for Inverse Problems

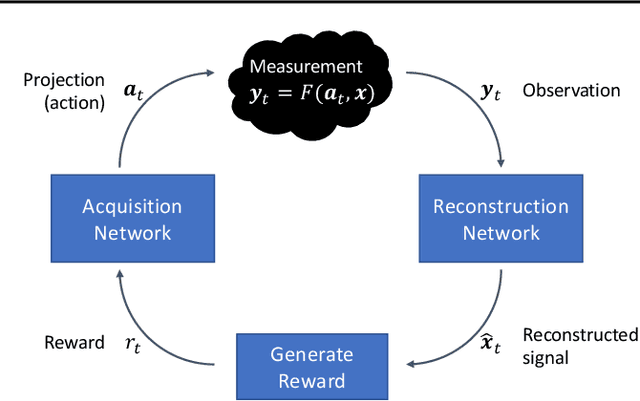
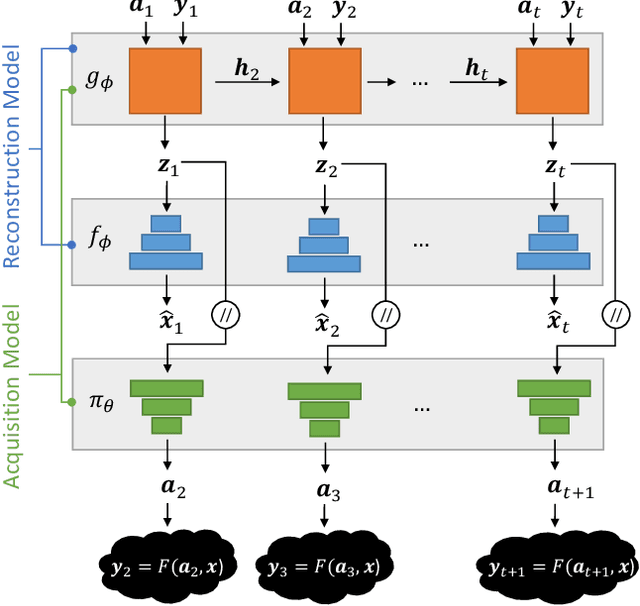
A promising way to mitigate the expensive process of obtaining a high-dimensional signal is to acquire a limited number of low-dimensional measurements and solve an under-determined inverse problem by utilizing the structural prior about the signal. In this paper, we focus on adaptive acquisition schemes to save further the number of measurements. To this end, we propose a reinforcement learning-based approach that sequentially collects measurements to better recover the underlying signal by acquiring fewer measurements. Our approach applies to general inverse problems with continuous action spaces and jointly learns the recovery algorithm. Using insights obtained from theoretical analysis, we also provide a probabilistic design for our methods using variational formulation. We evaluate our approach on multiple datasets and with two measurement spaces (Gaussian, Radon). Our results confirm the benefits of adaptive strategies in low-acquisition horizon settings.

Structure Learning in Graphical Models from Indirect Observations

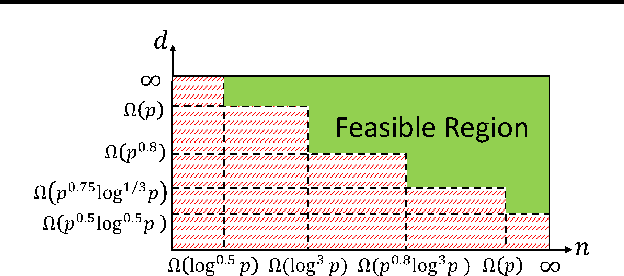
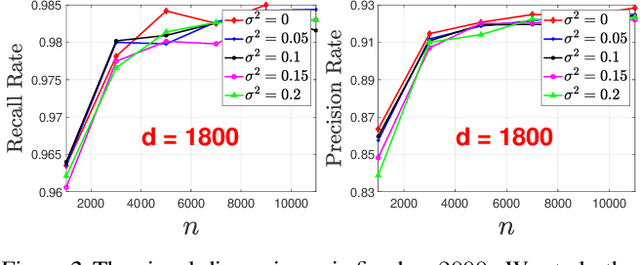
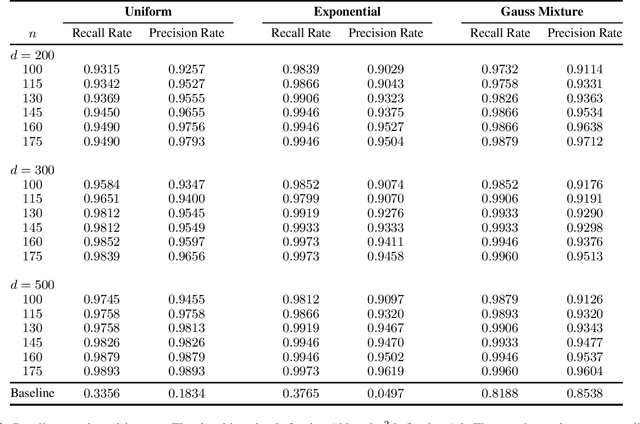
This paper considers learning of the graphical structure of a $p$-dimensional random vector $X \in R^p$ using both parametric and non-parametric methods. Unlike the previous works which observe $x$ directly, we consider the indirect observation scenario in which samples $y$ are collected via a sensing matrix $A \in R^{d\times p}$, and corrupted with some additive noise $w$, i.e, $Y = AX + W$. For the parametric method, we assume $X$ to be Gaussian, i.e., $x\in R^p\sim N(\mu, \Sigma)$ and $\Sigma \in R^{p\times p}$. For the first time, we show that the correct graphical structure can be correctly recovered under the indefinite sensing system ($d < p$) using insufficient samples ($n < p$). In particular, we show that for the exact recovery, we require dimension $d = \Omega(p^{0.8})$ and sample number $n = \Omega(p^{0.8}\log^3 p)$. For the nonparametric method, we assume a nonparanormal distribution for $X$ rather than Gaussian. Under mild conditions, we show that our graph-structure estimator can obtain the correct structure. We derive the minimum sample number $n$ and dimension $d$ as $n\gtrsim (deg)^4 \log^4 n$ and $d \gtrsim p + (deg\cdot\log(d-p))^{\beta/4}$, respectively, where deg is the maximum Markov blanket in the graphical model and $\beta > 0$ is some fixed positive constant. Additionally, we obtain a non-asymptotic uniform bound on the estimation error of the CDF of $X$ from indirect observations with inexact knowledge of the noise distribution. To the best of our knowledge, this bound is derived for the first time and may serve as an independent interest. Numerical experiments on both real-world and synthetic data are provided confirm the theoretical results.

A General Compressive Sensing Construct using Density Evolution

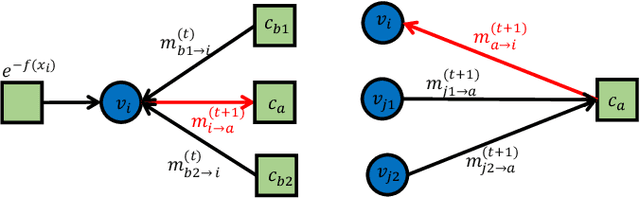
This paper proposes a general framework to design a sparse sensing matrix $\ensuremath{\mathbf{A}}\in \mathbb{R}^{m\times n}$, in a linear measurement system $\ensuremath{\mathbf{y}} = \ensuremath{\mathbf{Ax}}^{\natural} + \ensuremath{\mathbf{w}}$, where $\ensuremath{\mathbf{y}} \in \mathbb{R}^m$, $\ensuremath{\mathbf{x}}^{\natural}\in \RR^n$, and $\ensuremath{\mathbf{w}}$ denote the measurements, the signal with certain structures, and the measurement noise, respectively. By viewing the signal reconstruction from the measurements as a message passing algorithm over a graphical model, we leverage tools from coding theory in the design of low density parity check codes, namely the density evolution, and provide a framework for the design of matrix $\ensuremath{\mathbf{A}}$. Particularly, compared to the previous methods, our proposed framework enjoys the following desirable properties: ($i$) Universality: the design supports both regular sensing and preferential sensing, and incorporates them in a single framework; ($ii$) Flexibility: the framework can easily adapt the design of $\bA$ to a signal $\ensuremath{\mathbf{x}}^{\natural}$ with different underlying structures. As an illustration, we consider the $\ell_1$ regularizer, which correspond to Lasso, for both the regular sensing and preferential sensing scheme. Noteworthy, our framework can reproduce the classical result of Lasso, i.e., $m\geq c_0 k\log(n/k)$ (the regular sensing) with regular design after proper distribution approximation, where $c_0 > 0$ is some fixed constant. We also provide numerical experiments to confirm the analytical results and demonstrate the superiority of our framework whenever a preferential treatment of a sub-block of vector $\bx^{\natural}$ is required.

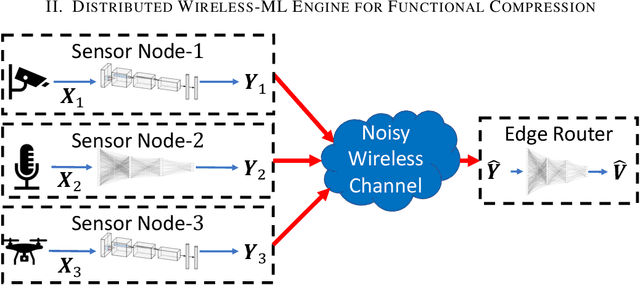
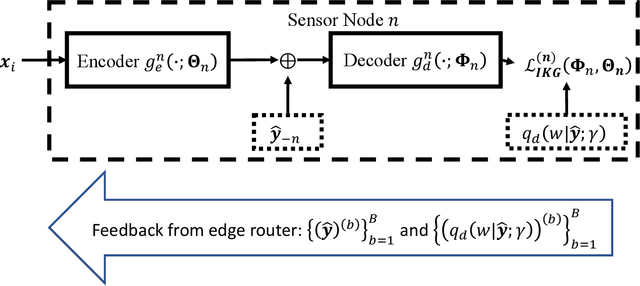
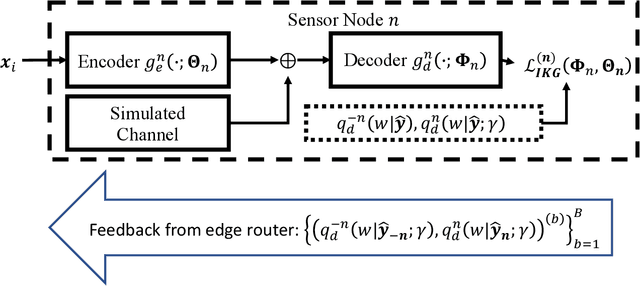
A Machine Learning Framework for Distributed Functional Compression over Wireless Channels in IoT

IoT devices generating enormous data and state-of-the-art machine learning techniques together will revolutionize cyber-physical systems. In many diverse fields, from autonomous driving to augmented reality, distributed IoT devices compute specific target functions without simple forms like obstacle detection, object recognition, etc. Traditional cloud-based methods that focus on transferring data to a central location either for training or inference place enormous strain on network resources. To address this, we develop, to the best of our knowledge, the first machine learning framework for distributed functional compression over both the Gaussian Multiple Access Channel (GMAC) and orthogonal AWGN channels. Due to the Kolmogorov-Arnold representation theorem, our machine learning framework can, by design, compute any arbitrary function for the desired functional compression task in IoT. Importantly the raw sensory data are never transferred to a central node for training or inference, thus reducing communication. For these algorithms, we provide theoretical convergence guarantees and upper bounds on communication. Our simulations show that the learned encoders and decoders for functional compression perform significantly better than traditional approaches, are robust to channel condition changes and sensor outages. Compared to the cloud-based scenario, our algorithms reduce channel use by two orders of magnitude.

Restructuring, Pruning, and Adjustment of Deep Models for Parallel Distributed Inference

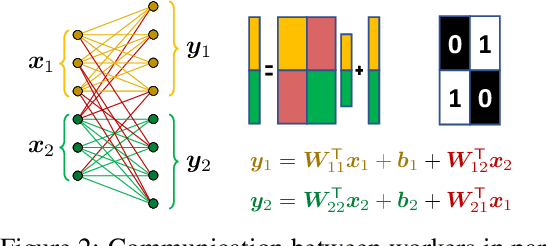
Using multiple nodes and parallel computing algorithms has become a principal tool to improve training and execution times of deep neural networks as well as effective collective intelligence in sensor networks. In this paper, we consider the parallel implementation of an already-trained deep model on multiple processing nodes (a.k.a. workers) where the deep model is divided into several parallel sub-models, each of which is executed by a worker. Since latency due to synchronization and data transfer among workers negatively impacts the performance of the parallel implementation, it is desirable to have minimum interdependency among parallel sub-models. To achieve this goal, we propose to rearrange the neurons in the neural network and partition them (without changing the general topology of the neural network), such that the interdependency among sub-models is minimized under the computations and communications constraints of the workers. We propose RePurpose, a layer-wise model restructuring and pruning technique that guarantees the performance of the overall parallelized model. To efficiently apply RePurpose, we propose an approach based on $\ell_0$ optimization and the Munkres assignment algorithm. We show that, compared to the existing methods, RePurpose significantly improves the efficiency of the distributed inference via parallel implementation, both in terms of communication and computational complexity.

Fast Convex Pruning of Deep Neural Networks

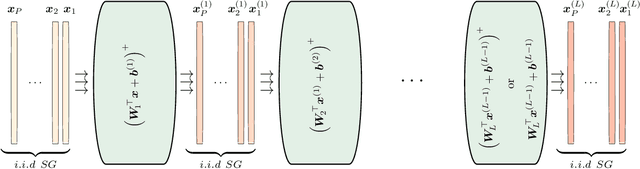
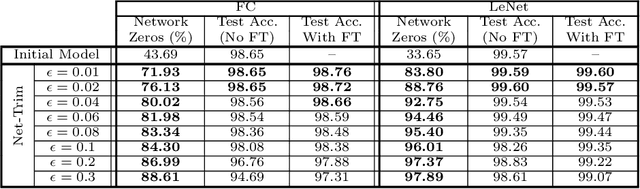
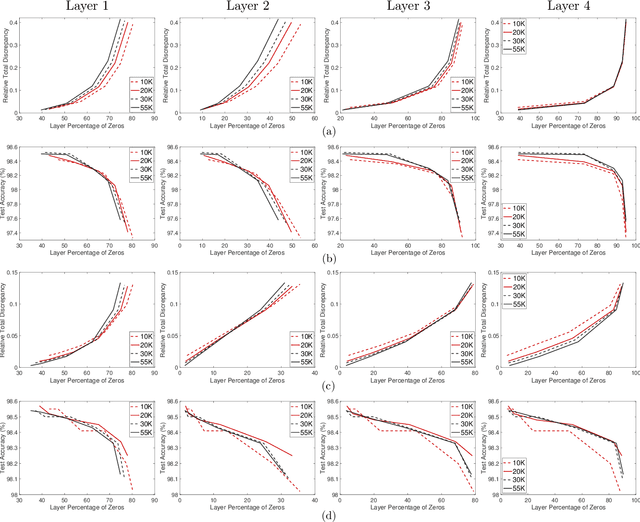
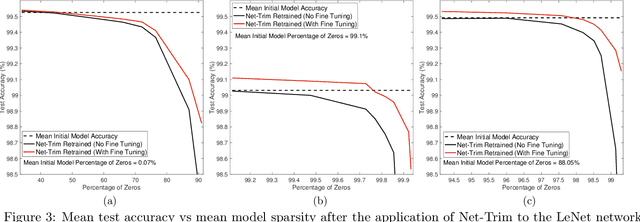
We develop a fast, tractable technique called Net-Trim for simplifying a trained neural network. The method is a convex post-processing module, which prunes (sparsifies) a trained network layer by layer, while preserving the internal responses. We present a comprehensive analysis of Net-Trim from both the algorithmic and sample complexity standpoints, centered on a fast, scalable convex optimization program. Our analysis includes consistency results between the initial and retrained models before and after Net-Trim application and guarantees on the number of training samples needed to discover a network that can be expressed using a certain number of nonzero terms. Specifically, if there is a set of weights that uses at most $s$ terms that can re-create the layer outputs from the layer inputs, we can find these weights from $\mathcal{O}(s\log N/s)$ samples, where $N$ is the input size. These theoretical results are similar to those for sparse regression using the Lasso, and our analysis uses some of the same recently-developed tools (namely recent results on the concentration of measure and convex analysis). Finally, we propose an algorithmic framework based on the alternating direction method of multipliers (ADMM), which allows a fast and simple implementation of Net-Trim for network pruning and compression.

Net-Trim: Convex Pruning of Deep Neural Networks with Performance Guarantee

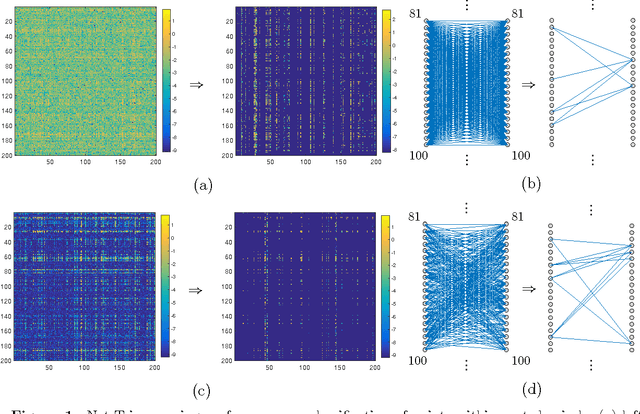
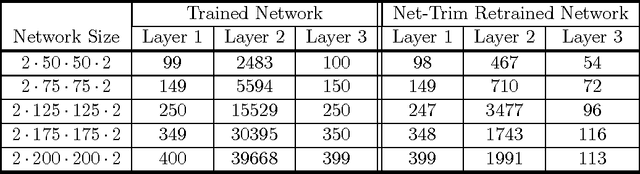
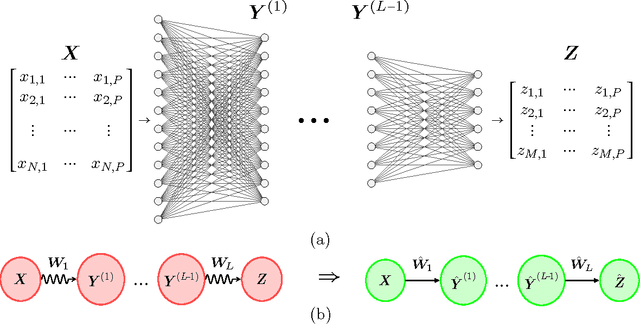
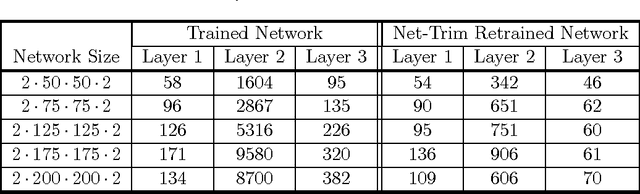
We introduce and analyze a new technique for model reduction for deep neural networks. While large networks are theoretically capable of learning arbitrarily complex models, overfitting and model redundancy negatively affects the prediction accuracy and model variance. Our Net-Trim algorithm prunes (sparsifies) a trained network layer-wise, removing connections at each layer by solving a convex optimization program. This program seeks a sparse set of weights at each layer that keeps the layer inputs and outputs consistent with the originally trained model. The algorithms and associated analysis are applicable to neural networks operating with the rectified linear unit (ReLU) as the nonlinear activation. We present both parallel and cascade versions of the algorithm. While the latter can achieve slightly simpler models with the same generalization performance, the former can be computed in a distributed manner. In both cases, Net-Trim significantly reduces the number of connections in the network, while also providing enough regularization to slightly reduce the generalization error. We also provide a mathematical analysis of the consistency between the initial network and the retrained model. To analyze the model sample complexity, we derive the general sufficient conditions for the recovery of a sparse transform matrix. For a single layer taking independent Gaussian random vectors of length $N$ as inputs, we show that if the network response can be described using a maximum number of $s$ non-zero weights per node, these weights can be learned from $\mathcal{O}(s\log N)$ samples.