Training Consistency Models with Variational Noise Coupling

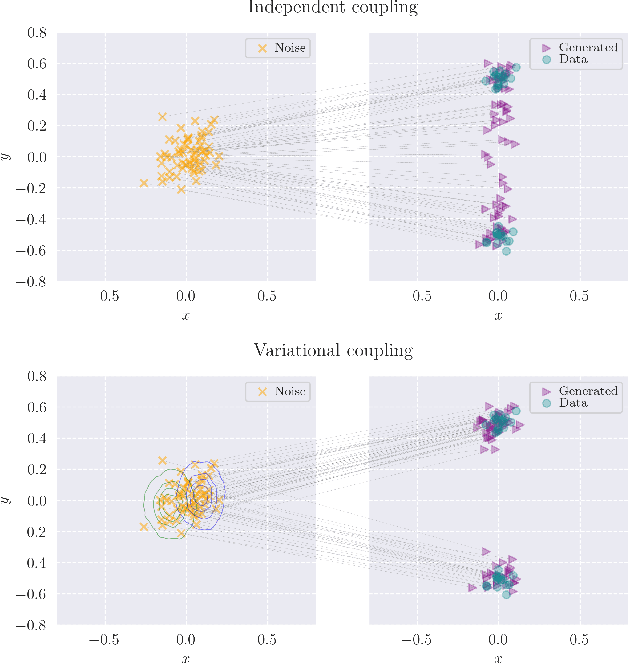
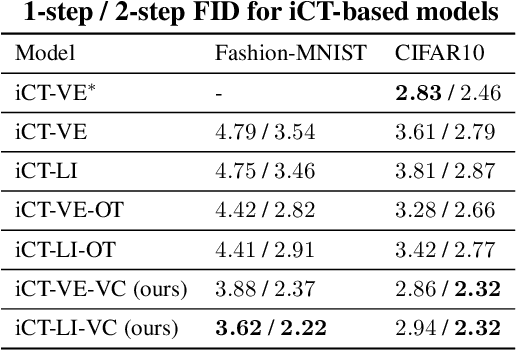
Consistency Training (CT) has recently emerged as a promising alternative to diffusion models, achieving competitive performance in image generation tasks. However, non-distillation consistency training often suffers from high variance and instability, and analyzing and improving its training dynamics is an active area of research. In this work, we propose a novel CT training approach based on the Flow Matching framework. Our main contribution is a trained noise-coupling scheme inspired by the architecture of Variational Autoencoders (VAE). By training a data-dependent noise emission model implemented as an encoder architecture, our method can indirectly learn the geometry of the noise-to-data mapping, which is instead fixed by the choice of the forward process in classical CT. Empirical results across diverse image datasets show significant generative improvements, with our model outperforming baselines and achieving the state-of-the-art (SoTA) non-distillation CT FID on CIFAR-10, and attaining FID on par with SoTA on ImageNet at $64 \times 64$ resolution in 2-step generation. Our code is available at https://github.com/sony/vct .

Losing dimensions: Geometric memorization in generative diffusion

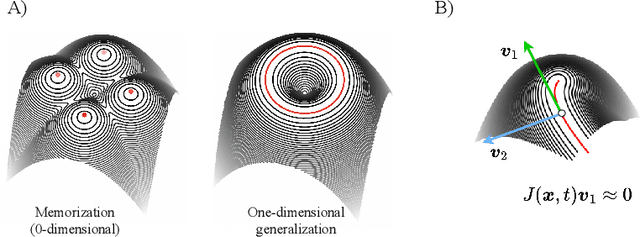
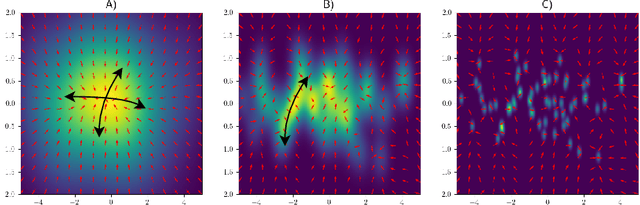
Generative diffusion processes are state-of-the-art machine learning models deeply connected with fundamental concepts in statistical physics. Depending on the dataset size and the capacity of the network, their behavior is known to transition from an associative memory regime to a generalization phase in a phenomenon that has been described as a glassy phase transition. Here, using statistical physics techniques, we extend the theory of memorization in generative diffusion to manifold-supported data. Our theoretical and experimental findings indicate that different tangent subspaces are lost due to memorization effects at different critical times and dataset sizes, which depend on the local variance of the data along their directions. Perhaps counterintuitively, we find that, under some conditions, subspaces of higher variance are lost first due to memorization effects. This leads to a selective loss of dimensionality where some prominent features of the data are memorized without a full collapse on any individual training point. We validate our theory with a comprehensive set of experiments on networks trained both in image datasets and on linear manifolds, which result in a remarkable qualitative agreement with the theoretical predictions.

Manifolds, Random Matrices and Spectral Gaps: The geometric phases of generative diffusion

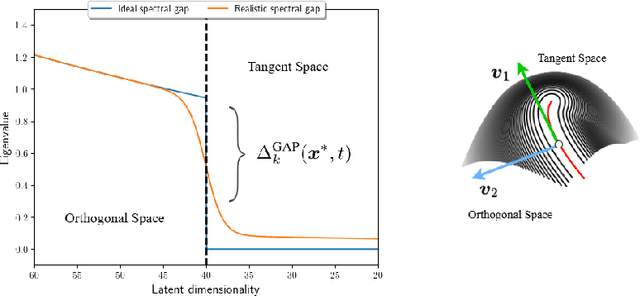
In this paper, we investigate the latent geometry of generative diffusion models under the manifold hypothesis. To this purpose, we analyze the spectrum of eigenvalues (and singular values) of the Jacobian of the score function, whose discontinuities (gaps) reveal the presence and dimensionality of distinct sub-manifolds. Using a statistical physics approach, we derive the spectral distributions and formulas for the spectral gaps under several distributional assumptions and we compare these theoretical predictions with the spectra estimated from trained networks. Our analysis reveals the existence of three distinct qualitative phases during the generative process: a trivial phase; a manifold coverage phase where the diffusion process fits the distribution internal to the manifold; a consolidation phase where the score becomes orthogonal to the manifold and all particles are projected on the support of the data. This `division of labor' between different timescales provides an elegant explanation on why generative diffusion models are not affected by the manifold overfitting phenomenon that plagues likelihood-based models, since the internal distribution and the manifold geometry are produced at different time points during generation.

Reinforcement Learning of Adaptive Acquisition Policies for Inverse Problems

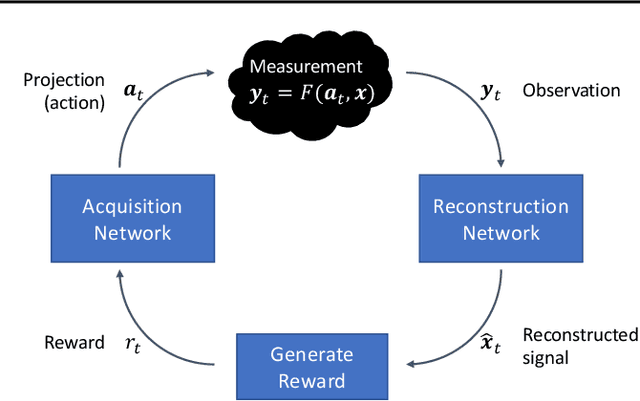
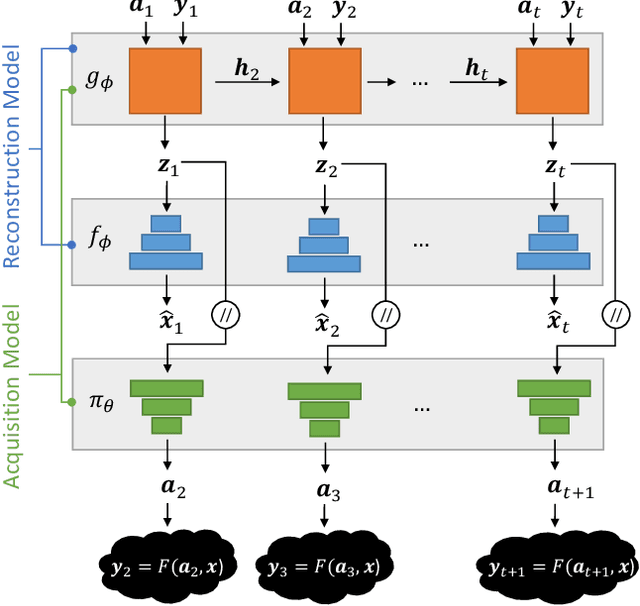
A promising way to mitigate the expensive process of obtaining a high-dimensional signal is to acquire a limited number of low-dimensional measurements and solve an under-determined inverse problem by utilizing the structural prior about the signal. In this paper, we focus on adaptive acquisition schemes to save further the number of measurements. To this end, we propose a reinforcement learning-based approach that sequentially collects measurements to better recover the underlying signal by acquiring fewer measurements. Our approach applies to general inverse problems with continuous action spaces and jointly learns the recovery algorithm. Using insights obtained from theoretical analysis, we also provide a probabilistic design for our methods using variational formulation. We evaluate our approach on multiple datasets and with two measurement spaces (Gaussian, Radon). Our results confirm the benefits of adaptive strategies in low-acquisition horizon settings.

Synthesizing EEG Signals from Event-Related Potential Paradigms with Conditional Diffusion Models

Data scarcity in the brain-computer interface field can be alleviated through the use of generative models, specifically diffusion models. While diffusion models have previously been successfully applied to electroencephalogram (EEG) data, existing models lack flexibility w.r.t.~sampling or require alternative representations of the EEG data. To overcome these limitations, we introduce a novel approach to conditional diffusion models that utilizes classifier-free guidance to directly generate subject-, session-, and class-specific EEG data. In addition to commonly used metrics, domain-specific metrics are employed to evaluate the specificity of the generated samples. The results indicate that the proposed model can generate EEG data that resembles real data for each subject, session, and class.

Closing the gap: Exact maximum likelihood training of generative autoencoders using invertible layers

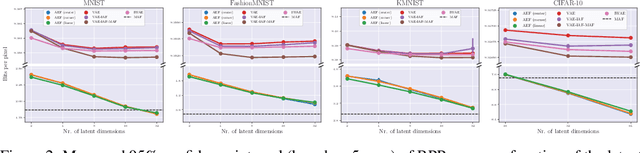
In this work, we provide an exact likelihood alternative to the variational training of generative autoencoders. We show that VAE-style autoencoders can be constructed using invertible layers, which offer a tractable exact likelihood without the need for any regularization terms. This is achieved while leaving complete freedom in the choice of encoder, decoder and prior architectures, making our approach a drop-in replacement for the training of existing VAEs and VAE-style models. We refer to the resulting models as Autoencoders within Flows (AEF), since the encoder, decoder and prior are defined as individual layers of an overall invertible architecture. We show that the approach results in strikingly higher performance than architecturally equivalent VAEs in term of log-likelihood, sample quality and denoising performance. In a broad sense, the main ambition of this work is to close the gap between the normalizing flow and autoencoder literature under the common framework of invertibility and exact maximum likelihood.

Embedded-model flows: Combining the inductive biases of model-free deep learning and explicit probabilistic modeling

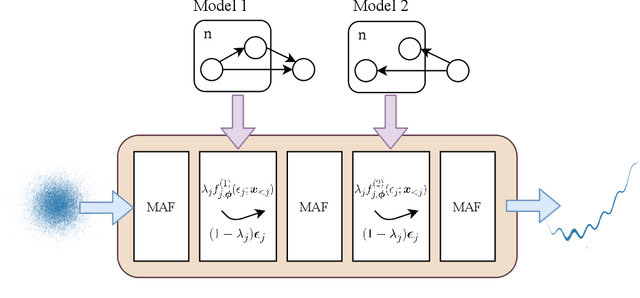
Normalizing flows have shown great success as general-purpose density estimators. However, many real world applications require the use of domain-specific knowledge, which normalizing flows cannot readily incorporate. We propose embedded-model flows (EMF), which alternate general-purpose transformations with structured layers that embed domain-specific inductive biases. These layers are automatically constructed by converting user-specified differentiable probabilistic models into equivalent bijective transformations. We also introduce gated structured layers, which allow bypassing the parts of the models that fail to capture the statistics of the data. We demonstrate that EMFs can be used to induce desirable properties such as multimodality, hierarchical coupling and continuity. Furthermore, we show that EMFs enable a high performance form of variational inference where the structure of the prior model is embedded in the variational architecture. In our experiments, we show that this approach outperforms state-of-the-art methods in common structured inference problems.

Automatic variational inference with cascading flows

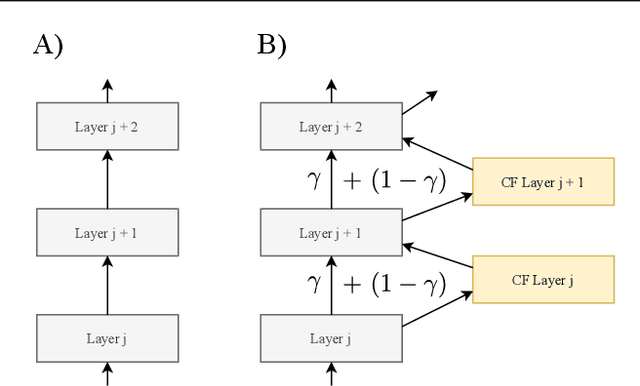
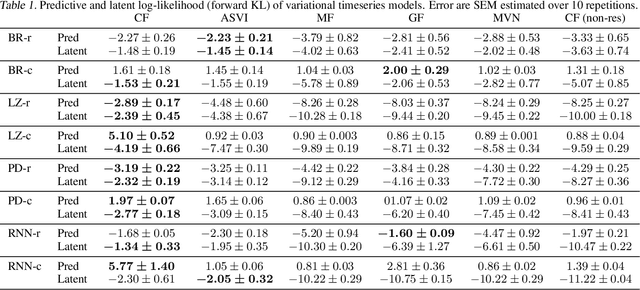
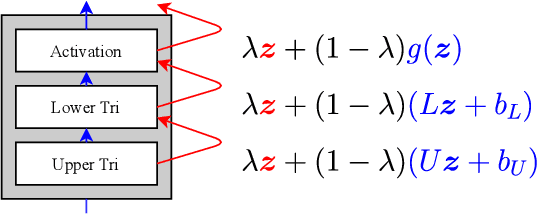
The automation of probabilistic reasoning is one of the primary aims of machine learning. Recently, the confluence of variational inference and deep learning has led to powerful and flexible automatic inference methods that can be trained by stochastic gradient descent. In particular, normalizing flows are highly parameterized deep models that can fit arbitrarily complex posterior densities. However, normalizing flows struggle in highly structured probabilistic programs as they need to relearn the forward-pass of the program. Automatic structured variational inference (ASVI) remedies this problem by constructing variational programs that embed the forward-pass. Here, we combine the flexibility of normalizing flows and the prior-embedding property of ASVI in a new family of variational programs, which we named cascading flows. A cascading flows program interposes a newly designed highway flow architecture in between the conditional distributions of the prior program such as to steer it toward the observed data. These programs can be constructed automatically from an input probabilistic program and can also be amortized automatically. We evaluate the performance of the new variational programs in a series of structured inference problems. We find that cascading flows have much higher performance than both normalizing flows and ASVI in a large set of structured inference problems.