Losing dimensions: Geometric memorization in generative diffusion

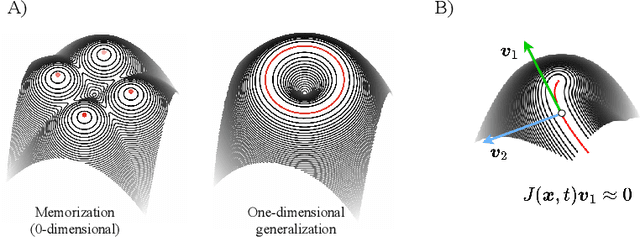
Generative diffusion processes are state-of-the-art machine learning models deeply connected with fundamental concepts in statistical physics. Depending on the dataset size and the capacity of the network, their behavior is known to transition from an associative memory regime to a generalization phase in a phenomenon that has been described as a glassy phase transition. Here, using statistical physics techniques, we extend the theory of memorization in generative diffusion to manifold-supported data. Our theoretical and experimental findings indicate that different tangent subspaces are lost due to memorization effects at different critical times and dataset sizes, which depend on the local variance of the data along their directions. Perhaps counterintuitively, we find that, under some conditions, subspaces of higher variance are lost first due to memorization effects. This leads to a selective loss of dimensionality where some prominent features of the data are memorized without a full collapse on any individual training point. We validate our theory with a comprehensive set of experiments on networks trained both in image datasets and on linear manifolds, which result in a remarkable qualitative agreement with the theoretical predictions.

Manifolds, Random Matrices and Spectral Gaps: The geometric phases of generative diffusion

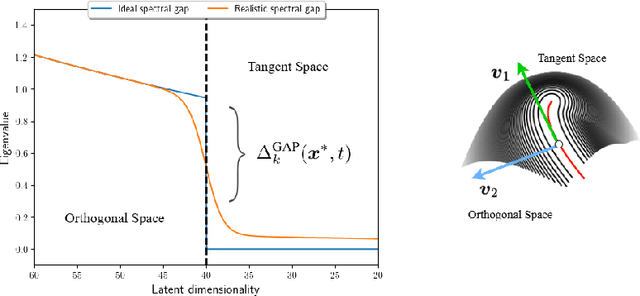
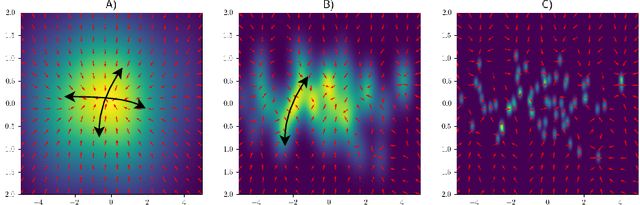
In this paper, we investigate the latent geometry of generative diffusion models under the manifold hypothesis. To this purpose, we analyze the spectrum of eigenvalues (and singular values) of the Jacobian of the score function, whose discontinuities (gaps) reveal the presence and dimensionality of distinct sub-manifolds. Using a statistical physics approach, we derive the spectral distributions and formulas for the spectral gaps under several distributional assumptions and we compare these theoretical predictions with the spectra estimated from trained networks. Our analysis reveals the existence of three distinct qualitative phases during the generative process: a trivial phase; a manifold coverage phase where the diffusion process fits the distribution internal to the manifold; a consolidation phase where the score becomes orthogonal to the manifold and all particles are projected on the support of the data. This `division of labor' between different timescales provides an elegant explanation on why generative diffusion models are not affected by the manifold overfitting phenomenon that plagues likelihood-based models, since the internal distribution and the manifold geometry are produced at different time points during generation.