Deep Clustering with Associative Memories

Deep clustering - joint representation learning and latent space clustering - is a well studied problem especially in computer vision and text processing under the deep learning framework. While the representation learning is generally differentiable, clustering is an inherently discrete optimization task, requiring various approximations and regularizations to fit in a standard differentiable pipeline. This leads to a somewhat disjointed representation learning and clustering. In this work, we propose a novel loss function utilizing energy-based dynamics via Associative Memories to formulate a new deep clustering method, DCAM, which ties together the representation learning and clustering aspects more intricately in a single objective. Our experiments showcase the advantage of DCAM, producing improved clustering quality for various architecture choices (convolutional, residual or fully-connected) and data modalities (images or text).

NRGPT: An Energy-based Alternative for GPT

Generative Pre-trained Transformer (GPT) architectures are the most popular design for language modeling. Energy-based modeling is a different paradigm that views inference as a dynamical process operating on an energy landscape. We propose a minimal modification of the GPT setting to unify it with the EBM framework. The inference step of our model, which we call eNeRgy-GPT (NRGPT), is conceptualized as an exploration of the tokens on the energy landscape. We prove, and verify empirically, that under certain circumstances this exploration becomes gradient descent, although they don't necessarily lead to the best performing models. We demonstrate that our model performs well for simple language (Shakespeare dataset), algebraic ListOPS tasks, and richer settings such as OpenWebText language modeling. We also observe that our models may be more resistant to overfitting, doing so only during very long training.

Dense Associative Memories with Analog Circuits

The increasing computational demands of modern AI systems have exposed fundamental limitations of digital hardware, driving interest in alternative paradigms for efficient large-scale inference. Dense Associative Memory (DenseAM) is a family of models that offers a flexible framework for representing many contemporary neural architectures, such as transformers and diffusion models, by casting them as dynamical systems evolving on an energy landscape. In this work, we propose a general method for building analog accelerators for DenseAMs and implementing them using electronic RC circuits, crossbar arrays, and amplifiers. We find that our analog DenseAM hardware performs inference in constant time independent of model size. This result highlights an asymptotic advantage of analog DenseAMs over digital numerical solvers that scale at least linearly with the model size. We consider three settings of progressively increasing complexity: XOR, the Hamming (7,4) code, and a simple language model defined on binary variables. We propose analog implementations of these three models and analyze the scaling of inference time, energy consumption, and hardware. Finally, we estimate lower bounds on the achievable time constants imposed by amplifier specifications, suggesting that even conservative existing analog technology can enable inference times on the order of tens to hundreds of nanoseconds. By harnessing the intrinsic parallelism and continuous-time operation of analog circuits, our DenseAM-based accelerator design offers a new avenue for fast and scalable AI hardware.

Modern Methods in Associative Memory

Associative Memories like the famous Hopfield Networks are elegant models for describing fully recurrent neural networks whose fundamental job is to store and retrieve information. In the past few years they experienced a surge of interest due to novel theoretical results pertaining to their information storage capabilities, and their relationship with SOTA AI architectures, such as Transformers and Diffusion Models. These connections open up possibilities for interpreting the computation of traditional AI networks through the theoretical lens of Associative Memories. Additionally, novel Lagrangian formulations of these networks make it possible to design powerful distributed models that learn useful representations and inform the design of novel architectures. This tutorial provides an approachable introduction to Associative Memories, emphasizing the modern language and methods used in this area of research, with practical hands-on mathematical derivations and coding notebooks.

Dense Associative Memory with Epanechnikov Energy

We propose a novel energy function for Dense Associative Memory (DenseAM) networks, the log-sum-ReLU (LSR), inspired by optimal kernel density estimation. Unlike the common log-sum-exponential (LSE) function, LSR is based on the Epanechnikov kernel and enables exact memory retrieval with exponential capacity without requiring exponential separation functions. Moreover, it introduces abundant additional \emph{emergent} local minima while preserving perfect pattern recovery -- a characteristic previously unseen in DenseAM literature. Empirical results show that LSR energy has significantly more local minima (memories) that have comparable log-likelihood to LSE-based models. Analysis of LSR's emergent memories on image datasets reveals a degree of creativity and novelty, hinting at this method's potential for both large-scale memory storage and generative tasks.

Memorization to Generalization: Emergence of Diffusion Models from Associative Memory

Hopfield networks are associative memory (AM) systems, designed for storing and retrieving patterns as local minima of an energy landscape. In the classical Hopfield model, an interesting phenomenon occurs when the amount of training data reaches its critical memory load $- spurious\,\,states$, or unintended stable points, emerge at the end of the retrieval dynamics, leading to incorrect recall. In this work, we examine diffusion models, commonly used in generative modeling, from the perspective of AMs. The training phase of diffusion model is conceptualized as memory encoding (training data is stored in the memory). The generation phase is viewed as an attempt of memory retrieval. In the small data regime the diffusion model exhibits a strong memorization phase, where the network creates distinct basins of attraction around each sample in the training set, akin to the Hopfield model below the critical memory load. In the large data regime, a different phase appears where an increase in the size of the training set fosters the creation of new attractor states that correspond to manifolds of the generated samples. Spurious states appear at the boundary of this transition and correspond to emergent attractor states, which are absent in the training set, but, at the same time, have distinct basins of attraction around them. Our findings provide: a novel perspective on the memorization-generalization phenomenon in diffusion models via the lens of AMs, theoretical prediction of existence of spurious states, empirical validation of this prediction in commonly-used diffusion models.

Small Models, Smarter Learning: The Power of Joint Task Training

The ability of a model to learn a task depends strongly on both the task difficulty and the model size. We aim to understand how task difficulty relates to the minimum number of parameters required for learning specific tasks in small transformer models. Our study focuses on the ListOps dataset, which consists of nested mathematical operations. We gradually increase task difficulty by introducing new operations or combinations of operations into the training data. We observe that sum modulo n is the hardest to learn. Curiously, when combined with other operations such as maximum and median, the sum operation becomes easier to learn and requires fewer parameters. We show that joint training not only improves performance but also leads to qualitatively different model behavior. We show evidence that models trained only on SUM might be memorizing and fail to capture the number structure in the embeddings. In contrast, models trained on a mixture of SUM and other operations exhibit number-like representations in the embedding space, and a strong ability to distinguish parity. Furthermore, the SUM-only model relies more heavily on its feedforward layers, while the jointly trained model activates the attention mechanism more. Finally, we show that learning pure SUM can be induced in models below the learning threshold of pure SUM, by pretraining them on MAX+MED. Our findings indicate that emergent abilities in language models depend not only on model size, but also the training curriculum.

Dense Associative Memory Through the Lens of Random Features

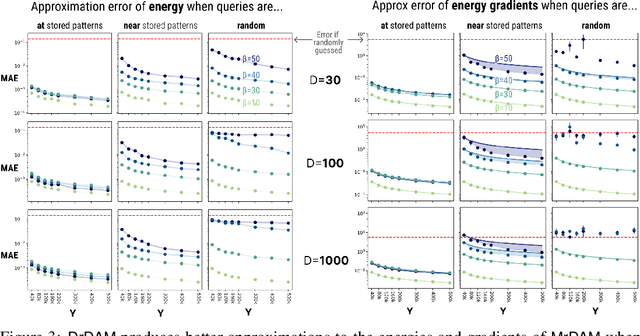
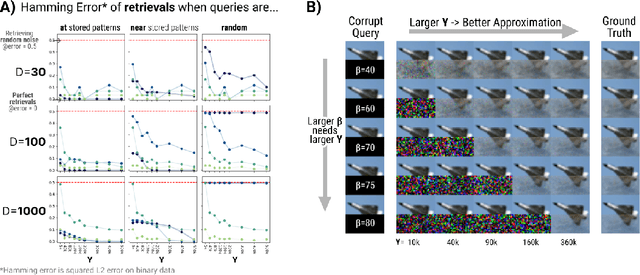
Dense Associative Memories are high storage capacity variants of the Hopfield networks that are capable of storing a large number of memory patterns in the weights of the network of a given size. Their common formulations typically require storing each pattern in a separate set of synaptic weights, which leads to the increase of the number of synaptic weights when new patterns are introduced. In this work we propose an alternative formulation of this class of models using random features, commonly used in kernel methods. In this formulation the number of network's parameters remains fixed. At the same time, new memories can be added to the network by modifying existing weights. We show that this novel network closely approximates the energy function and dynamics of conventional Dense Associative Memories and shares their desirable computational properties.

Losing dimensions: Geometric memorization in generative diffusion

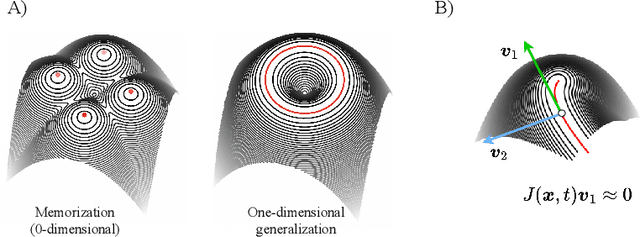
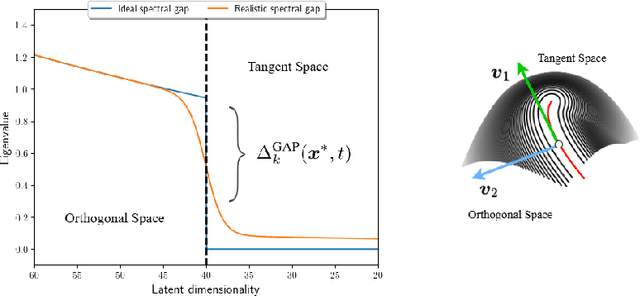
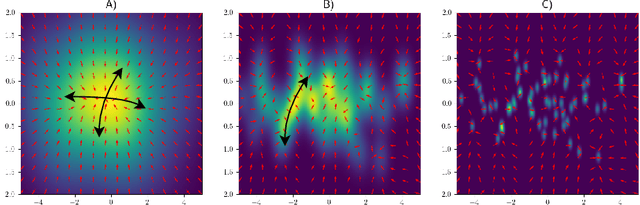
Generative diffusion processes are state-of-the-art machine learning models deeply connected with fundamental concepts in statistical physics. Depending on the dataset size and the capacity of the network, their behavior is known to transition from an associative memory regime to a generalization phase in a phenomenon that has been described as a glassy phase transition. Here, using statistical physics techniques, we extend the theory of memorization in generative diffusion to manifold-supported data. Our theoretical and experimental findings indicate that different tangent subspaces are lost due to memorization effects at different critical times and dataset sizes, which depend on the local variance of the data along their directions. Perhaps counterintuitively, we find that, under some conditions, subspaces of higher variance are lost first due to memorization effects. This leads to a selective loss of dimensionality where some prominent features of the data are memorized without a full collapse on any individual training point. We validate our theory with a comprehensive set of experiments on networks trained both in image datasets and on linear manifolds, which result in a remarkable qualitative agreement with the theoretical predictions.

CAMELoT: Towards Large Language Models with Training-Free Consolidated Associative Memory

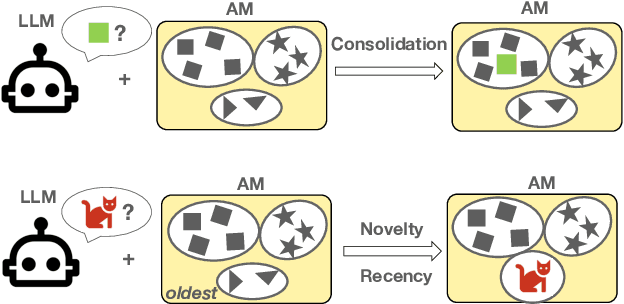
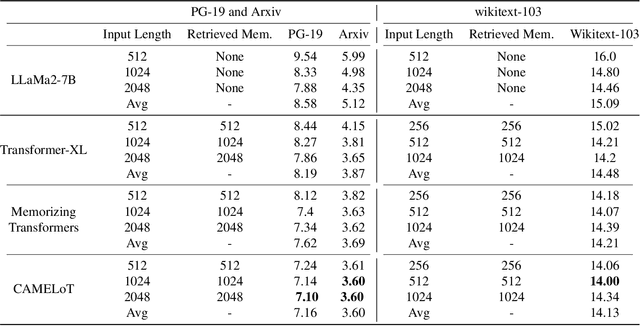
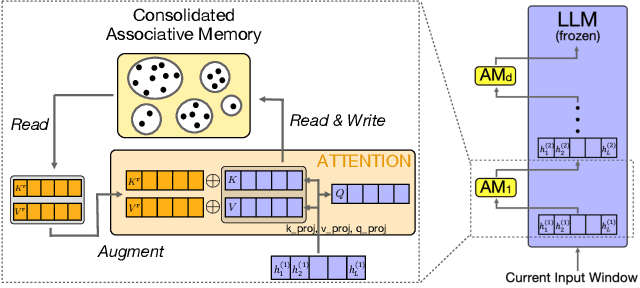
Large Language Models (LLMs) struggle to handle long input sequences due to high memory and runtime costs. Memory-augmented models have emerged as a promising solution to this problem, but current methods are hindered by limited memory capacity and require costly re-training to integrate with a new LLM. In this work, we introduce an associative memory module which can be coupled to any pre-trained (frozen) attention-based LLM without re-training, enabling it to handle arbitrarily long input sequences. Unlike previous methods, our associative memory module consolidates representations of individual tokens into a non-parametric distribution model, dynamically managed by properly balancing the novelty and recency of the incoming data. By retrieving information from this consolidated associative memory, the base LLM can achieve significant (up to 29.7% on Arxiv) perplexity reduction in long-context modeling compared to other baselines evaluated on standard benchmarks. This architecture, which we call CAMELoT (Consolidated Associative Memory Enhanced Long Transformer), demonstrates superior performance even with a tiny context window of 128 tokens, and also enables improved in-context learning with a much larger set of demonstrations.