Enrico Ventura
Emergence of Distortions in High-Dimensional Guided Diffusion Models
Jan 31, 2026Abstract:Classifier-free guidance (CFG) is the de facto standard for conditional sampling in diffusion models, yet it often leads to a loss of diversity in generated samples. We formalize this phenomenon as generative distortion, defined as the mismatch between the CFG-induced sampling distribution and the true conditional distribution. Considering Gaussian mixtures and their exact scores, and leveraging tools from statistical physics, we characterize the onset of distortion in a high-dimensional regime as a function of the number of classes. Our analysis reveals that distortions emerge through a phase transition in the effective potential governing the guided dynamics. In particular, our dynamical mean-field analysis shows that distortion persists when the number of modes grows exponentially with dimension, but vanishes in the sub-exponential regime. Consistent with prior finite-dimensional results, we further demonstrate that vanilla CFG shifts the mean and shrinks the variance of the conditional distribution. We show that standard CFG schedules are fundamentally incapable of preventing variance shrinkage. Finally, we propose a theoretically motivated guidance schedule featuring a negative-guidance window, which mitigates loss of diversity while preserving class separability.
Losing dimensions: Geometric memorization in generative diffusion
Oct 11, 2024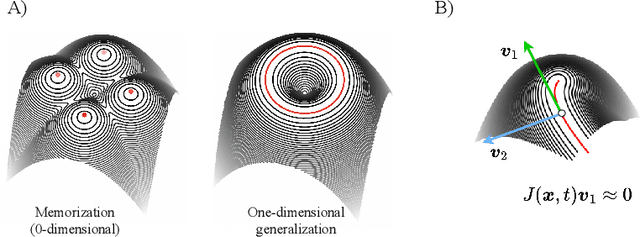

Abstract:Generative diffusion processes are state-of-the-art machine learning models deeply connected with fundamental concepts in statistical physics. Depending on the dataset size and the capacity of the network, their behavior is known to transition from an associative memory regime to a generalization phase in a phenomenon that has been described as a glassy phase transition. Here, using statistical physics techniques, we extend the theory of memorization in generative diffusion to manifold-supported data. Our theoretical and experimental findings indicate that different tangent subspaces are lost due to memorization effects at different critical times and dataset sizes, which depend on the local variance of the data along their directions. Perhaps counterintuitively, we find that, under some conditions, subspaces of higher variance are lost first due to memorization effects. This leads to a selective loss of dimensionality where some prominent features of the data are memorized without a full collapse on any individual training point. We validate our theory with a comprehensive set of experiments on networks trained both in image datasets and on linear manifolds, which result in a remarkable qualitative agreement with the theoretical predictions.
Manifolds, Random Matrices and Spectral Gaps: The geometric phases of generative diffusion
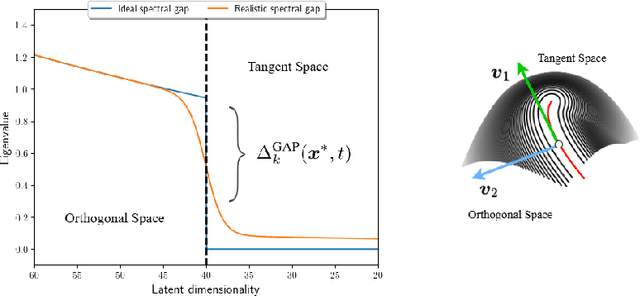
Oct 08, 2024



Abstract:In this paper, we investigate the latent geometry of generative diffusion models under the manifold hypothesis. To this purpose, we analyze the spectrum of eigenvalues (and singular values) of the Jacobian of the score function, whose discontinuities (gaps) reveal the presence and dimensionality of distinct sub-manifolds. Using a statistical physics approach, we derive the spectral distributions and formulas for the spectral gaps under several distributional assumptions and we compare these theoretical predictions with the spectra estimated from trained networks. Our analysis reveals the existence of three distinct qualitative phases during the generative process: a trivial phase; a manifold coverage phase where the diffusion process fits the distribution internal to the manifold; a consolidation phase where the score becomes orthogonal to the manifold and all particles are projected on the support of the data. This `division of labor' between different timescales provides an elegant explanation on why generative diffusion models are not affected by the manifold overfitting phenomenon that plagues likelihood-based models, since the internal distribution and the manifold geometry are produced at different time points during generation.
Demolition and Reinforcement of Memories in Spin-Glass-like Neural Networks
Mar 04, 2024Abstract:Statistical mechanics has made significant contributions to the study of biological neural systems by modeling them as recurrent networks of interconnected units with adjustable interactions. Several algorithms have been proposed to optimize the neural connections to enable network tasks such as information storage (i.e. associative memory) and learning probability distributions from data (i.e. generative modeling). Among these methods, the Unlearning algorithm, aligned with emerging theories of synaptic plasticity, was introduced by John Hopfield and collaborators. The primary objective of this thesis is to understand the effectiveness of Unlearning in both associative memory models and generative models. Initially, we demonstrate that the Unlearning algorithm can be simplified to a linear perceptron model which learns from noisy examples featuring specific internal correlations. The selection of structured training data enables an associative memory model to retrieve concepts as attractors of a neural dynamics with considerable basins of attraction. Subsequently, a novel regularization technique for Boltzmann Machines is presented, proving to outperform previously developed methods in learning hidden probability distributions from data-sets. The Unlearning rule is derived from this new regularized algorithm and is showed to be comparable, in terms of inferential performance, to traditional Boltzmann-Machine learning.
Training neural networks with structured noise improves classification and generalization
Mar 02, 2023Abstract:The beneficial role of noise in learning is nowadays a consolidated concept in the field of artificial neural networks. The training-with-noise algorithm proposed by Gardner and collaborators is an emblematic example of a noise injection procedure in recurrent networks. We show how adding structure into noisy training data can substantially improve memory performance, allowing to approach perfect classification and maximal basins of attraction. We also prove that the so-called unlearning rule coincides with the training-with-noise algorithm when noise is maximal and data are fixed points of the network dynamics. Moreover, a sampling scheme for optimal noisy data is proposed and implemented to outperform both the training-with-noise and the unlearning procedures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge