Carlo Lucibello
Sampling through Algorithmic Diffusion in non-convex Perceptron problems
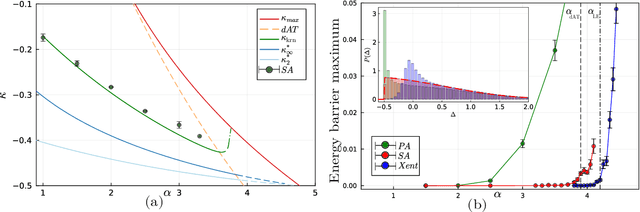
Feb 22, 2025Abstract:We analyze the problem of sampling from the solution space of simple yet non-convex neural network models by employing a denoising diffusion process known as Algorithmic Stochastic Localization, where the score function is provided by Approximate Message Passing. We introduce a formalism based on the replica method to characterize the process in the infinite-size limit in terms of a few order parameters, and, in particular, we provide criteria for the feasibility of sampling. We show that, in the case of the spherical perceptron problem with negative stability, approximate uniform sampling is achievable across the entire replica symmetric region of the phase diagram. In contrast, for the binary perceptron, uniform sampling via diffusion invariably fails due to the overlap gap property exhibited by the typical set of solutions. We discuss the first steps in defining alternative measures that can be efficiently sampled.
GraphNeuralNetworks.jl: Deep Learning on Graphs with Julia
Dec 09, 2024Abstract:GraphNeuralNetworks.jl is an open-source framework for deep learning on graphs, written in the Julia programming language. It supports multiple GPU backends, generic sparse or dense graph representations, and offers convenient interfaces for manipulating standard, heterogeneous, and temporal graphs with attributes at the node, edge, and graph levels. The framework allows users to define custom graph convolutional layers using gather/scatter message-passing primitives or optimized fused operations. It also includes several popular layers, enabling efficient experimentation with complex deep architectures. The package is available on GitHub: \url{https://github.com/JuliaGraphs/GraphNeuralNetworks.jl}.
Losing dimensions: Geometric memorization in generative diffusion
Oct 11, 2024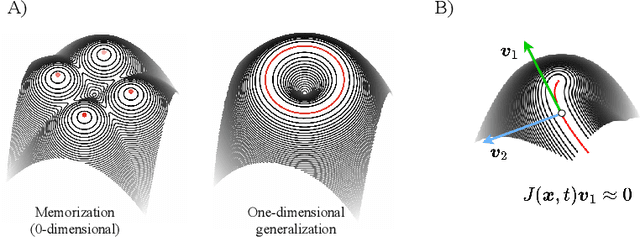

Abstract:Generative diffusion processes are state-of-the-art machine learning models deeply connected with fundamental concepts in statistical physics. Depending on the dataset size and the capacity of the network, their behavior is known to transition from an associative memory regime to a generalization phase in a phenomenon that has been described as a glassy phase transition. Here, using statistical physics techniques, we extend the theory of memorization in generative diffusion to manifold-supported data. Our theoretical and experimental findings indicate that different tangent subspaces are lost due to memorization effects at different critical times and dataset sizes, which depend on the local variance of the data along their directions. Perhaps counterintuitively, we find that, under some conditions, subspaces of higher variance are lost first due to memorization effects. This leads to a selective loss of dimensionality where some prominent features of the data are memorized without a full collapse on any individual training point. We validate our theory with a comprehensive set of experiments on networks trained both in image datasets and on linear manifolds, which result in a remarkable qualitative agreement with the theoretical predictions.
Manifolds, Random Matrices and Spectral Gaps: The geometric phases of generative diffusion
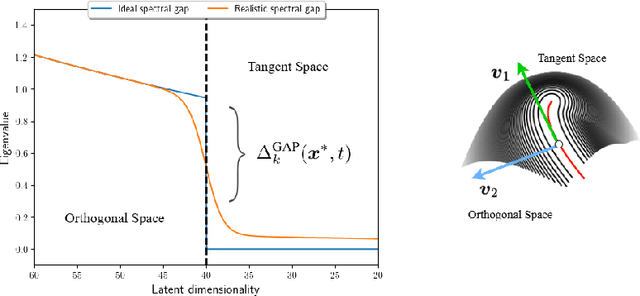
Oct 08, 2024Abstract:In this paper, we investigate the latent geometry of generative diffusion models under the manifold hypothesis. To this purpose, we analyze the spectrum of eigenvalues (and singular values) of the Jacobian of the score function, whose discontinuities (gaps) reveal the presence and dimensionality of distinct sub-manifolds. Using a statistical physics approach, we derive the spectral distributions and formulas for the spectral gaps under several distributional assumptions and we compare these theoretical predictions with the spectra estimated from trained networks. Our analysis reveals the existence of three distinct qualitative phases during the generative process: a trivial phase; a manifold coverage phase where the diffusion process fits the distribution internal to the manifold; a consolidation phase where the score becomes orthogonal to the manifold and all particles are projected on the support of the data. This `division of labor' between different timescales provides an elegant explanation on why generative diffusion models are not affected by the manifold overfitting phenomenon that plagues likelihood-based models, since the internal distribution and the manifold geometry are produced at different time points during generation.
Random Features Hopfield Networks generalize retrieval to previously unseen examples
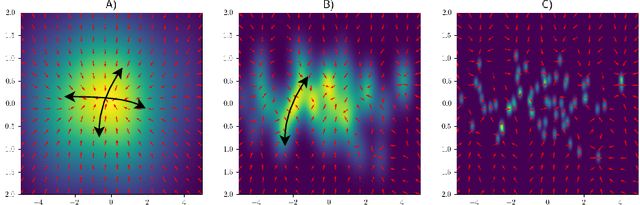
Jul 08, 2024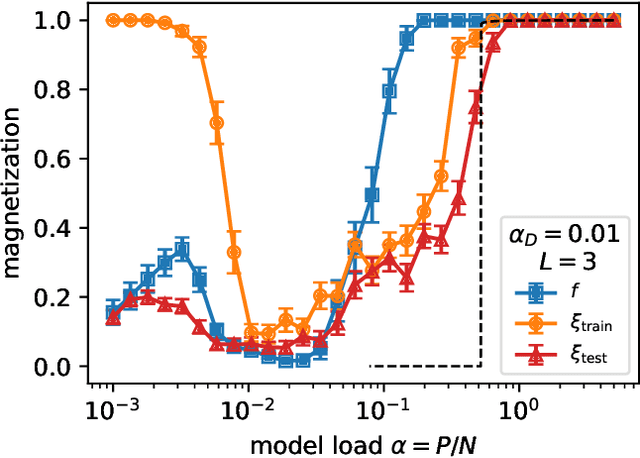
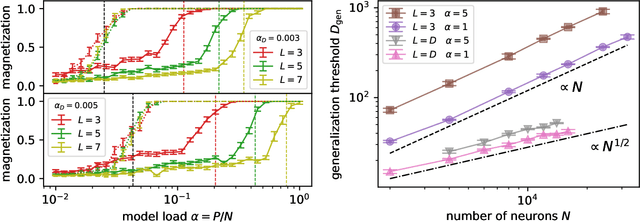
Abstract:It has been recently shown that a learning transition happens when a Hopfield Network stores examples generated as superpositions of random features, where new attractors corresponding to such features appear in the model. In this work we reveal that the network also develops attractors corresponding to previously unseen examples generated with the same set of features. We explain this surprising behaviour in terms of spurious states of the learned features: we argue that, increasing the number of stored examples beyond the learning transition, the model also learns to mix the features to represent both stored and previously unseen examples. We support this claim with the computation of the phase diagram of the model.
The star-shaped space of solutions of the spherical negative perceptron
May 18, 2023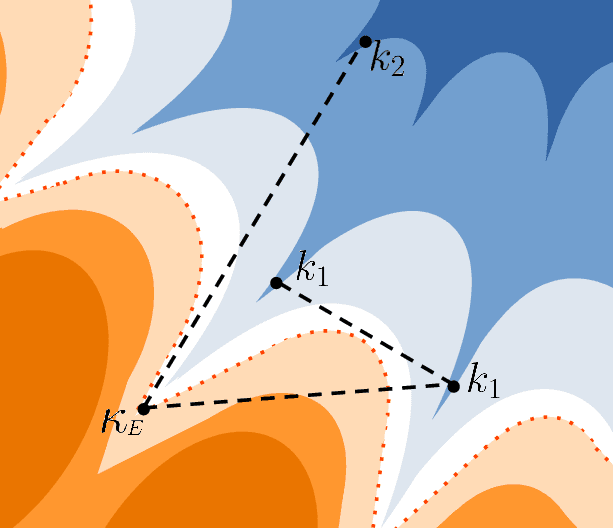
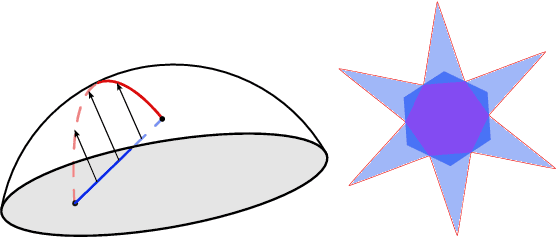
Abstract:Empirical studies on the landscape of neural networks have shown that low-energy configurations are often found in complex connected structures, where zero-energy paths between pairs of distant solutions can be constructed. Here we consider the spherical negative perceptron, a prototypical non-convex neural network model framed as a continuous constraint satisfaction problem. We introduce a general analytical method for computing energy barriers in the simplex with vertex configurations sampled from the equilibrium. We find that in the over-parameterized regime the solution manifold displays simple connectivity properties. There exists a large geodesically convex component that is attractive for a wide range of optimization dynamics. Inside this region we identify a subset of atypically robust solutions that are geodesically connected with most other solutions, giving rise to a star-shaped geometry. We analytically characterize the organization of the connected space of solutions and show numerical evidence of a transition, at larger constraint densities, where the aforementioned simple geodesic connectivity breaks down.
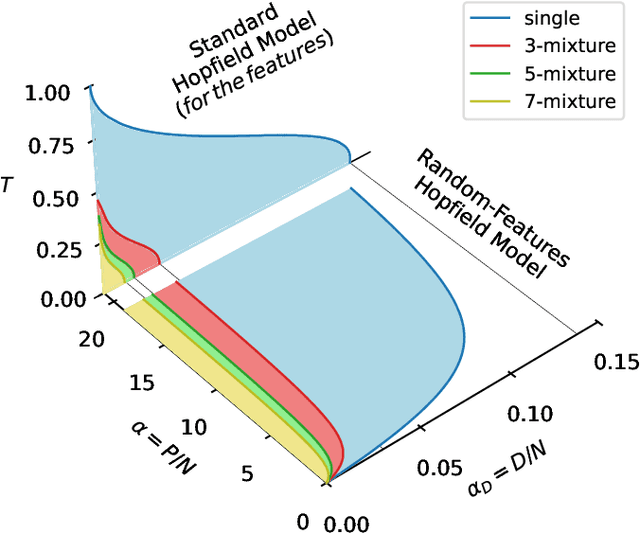
The Hidden-Manifold Hopfield Model and a learning phase transition
Mar 29, 2023



Abstract:The Hopfield model has a long-standing tradition in statistical physics, being one of the few neural networks for which a theory is available. Extending the theory of Hopfield models for correlated data could help understand the success of deep neural networks, for instance describing how they extract features from data. Motivated by this, we propose and investigate a generalized Hopfield model that we name Hidden-Manifold Hopfield Model: we generate the couplings from $P=\alpha N$ examples with the Hebb rule using a non-linear transformation of $D=\alpha_D N$ random vectors that we call factors, with $N$ the number of neurons. Using the replica method, we obtain a phase diagram for the model that shows a phase transition where the factors hidden in the examples become attractors of the dynamics; this phase exists above a critical value of $\alpha$ and below a critical value of $\alpha_D$. We call this behaviour learning transition.
Noise-cleaning the precision matrix of fMRI time series
Feb 06, 2023Abstract:We present a comparison between various algorithms of inference of covariance and precision matrices in small datasets of real vectors, of the typical length and dimension of human brain activity time series retrieved by functional Magnetic Resonance Imaging (fMRI). Assuming a Gaussian model underlying the neural activity, the problem consists in denoising the empirically observed matrices in order to obtain a better estimator of the true precision and covariance matrices. We consider several standard noise-cleaning algorithms and compare them on two types of datasets. The first type are time series of fMRI brain activity of human subjects at rest. The second type are synthetic time series sampled from a generative Gaussian model of which we can vary the fraction of dimensions per sample q = N/T and the strength of off-diagonal correlations. The reliability of each algorithm is assessed in terms of test-set likelihood and, in the case of synthetic data, of the distance from the true precision matrix. We observe that the so called Optimal Rotationally Invariant Estimator, based on Random Matrix Theory, leads to a significantly lower distance from the true precision matrix in synthetic data, and higher test likelihood in natural fMRI data. We propose a variant of the Optimal Rotationally Invariant Estimator in which one of its parameters is optimised by cross-validation. In the severe undersampling regime (large q) typical of fMRI series, it outperforms all the other estimators. We furthermore propose a simple algorithm based on an iterative likelihood gradient ascent, providing an accurate estimation for weakly correlated datasets.
Deep learning via message passing algorithms based on belief propagation
Oct 27, 2021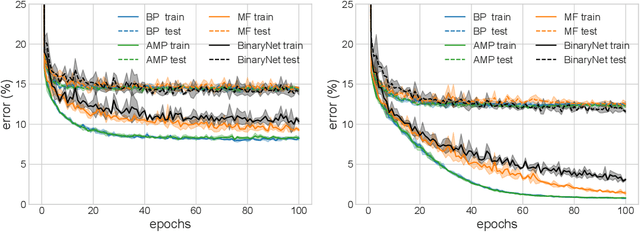

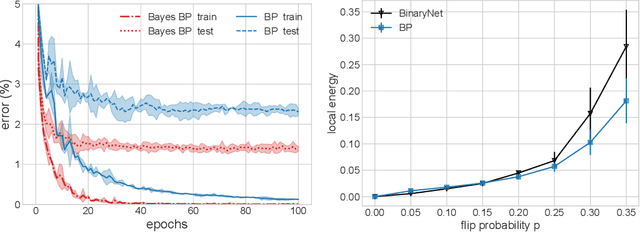

Abstract:Message-passing algorithms based on the Belief Propagation (BP) equations constitute a well-known distributed computational scheme. It is exact on tree-like graphical models and has also proven to be effective in many problems defined on graphs with loops (from inference to optimization, from signal processing to clustering). The BP-based scheme is fundamentally different from stochastic gradient descent (SGD), on which the current success of deep networks is based. In this paper, we present and adapt to mini-batch training on GPUs a family of BP-based message-passing algorithms with a reinforcement field that biases distributions towards locally entropic solutions. These algorithms are capable of training multi-layer neural networks with discrete weights and activations with performance comparable to SGD-inspired heuristics (BinaryNet) and are naturally well-adapted to continual learning. Furthermore, using these algorithms to estimate the marginals of the weights allows us to make approximate Bayesian predictions that have higher accuracy than point-wise solutions.
Reconstruction of Pairwise Interactions using Energy-Based Models
Dec 11, 2020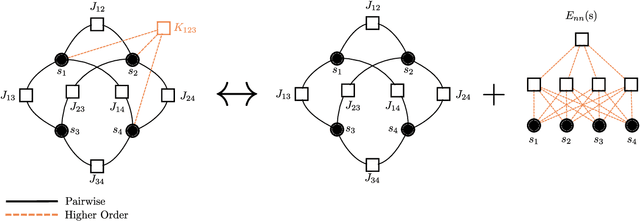
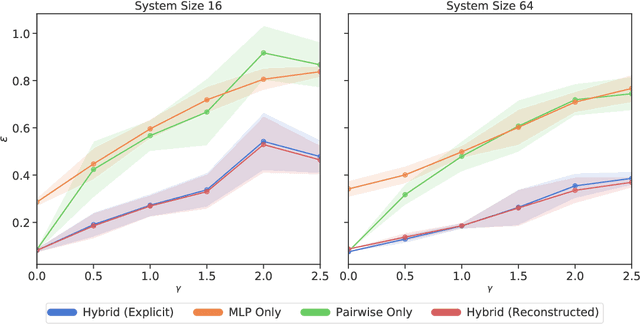
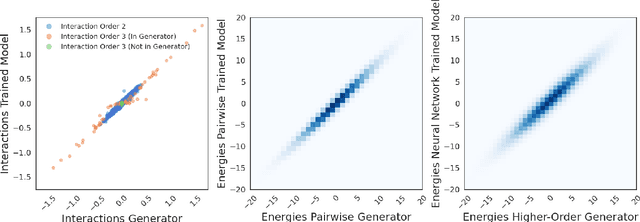
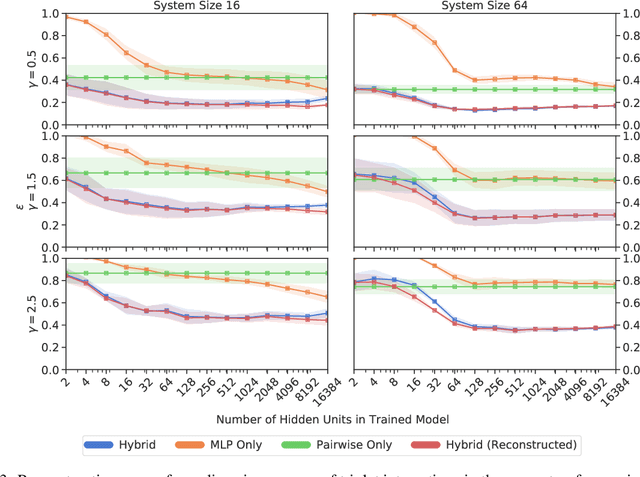
Abstract:Pairwise models like the Ising model or the generalized Potts model have found many successful applications in fields like physics, biology, and economics. Closely connected is the problem of inverse statistical mechanics, where the goal is to infer the parameters of such models given observed data. An open problem in this field is the question of how to train these models in the case where the data contain additional higher-order interactions that are not present in the pairwise model. In this work, we propose an approach based on Energy-Based Models and pseudolikelihood maximization to address these complications: we show that hybrid models, which combine a pairwise model and a neural network, can lead to significant improvements in the reconstruction of pairwise interactions. We show these improvements to hold consistently when compared to a standard approach using only the pairwise model and to an approach using only a neural network. This is in line with the general idea that simple interpretable models and complex black-box models are not necessarily a dichotomy: interpolating these two classes of models can allow to keep some advantages of both.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge