Enrico M. Malatesta
Exact full-RSB SAT/UNSAT transition in infinitely wide two-layer neural networks
Oct 09, 2024



Abstract:We analyze the problem of storing random pattern-label associations using two classes of continuous non-convex weights models, namely the perceptron with negative margin and an infinite width two layer neural network with non-overlapping receptive fields and generic activation function. Using a full-RSB ansatz we compute the exact value of the SAT/UNSAT transition. Furthermore, in the case of the negative perceptron model we show that, depending on the value of the margin and the constrained density, there is a line separating a phase in which the distribution of overlaps of typical states does not possess a gap from one in which it does. Our results show that the hypothesis underlying some recently developed theorems claiming that Approximate Message Passing (AMP) based algorithms are able to reach capacity, does not hold in general. Finally, we show that Gradient Descent is not able to reach the maximal capacity both in cases where there is and there is not a non-overlap gap phase for the typical states. This, similarly to what occurs in binary weight models, suggests that gradient-based algorithms are biased towards highly atypical states, whose inaccessibility determines the algorithmic threshold.
Random Features Hopfield Networks generalize retrieval to previously unseen examples
Jul 08, 2024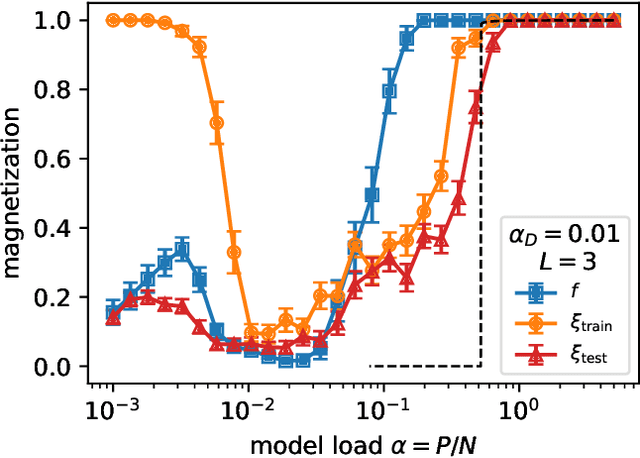
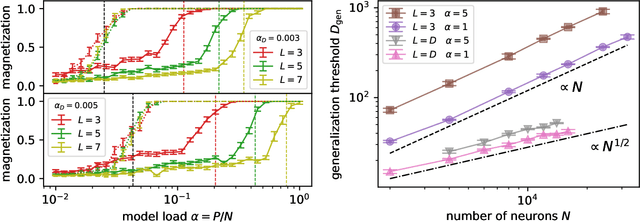
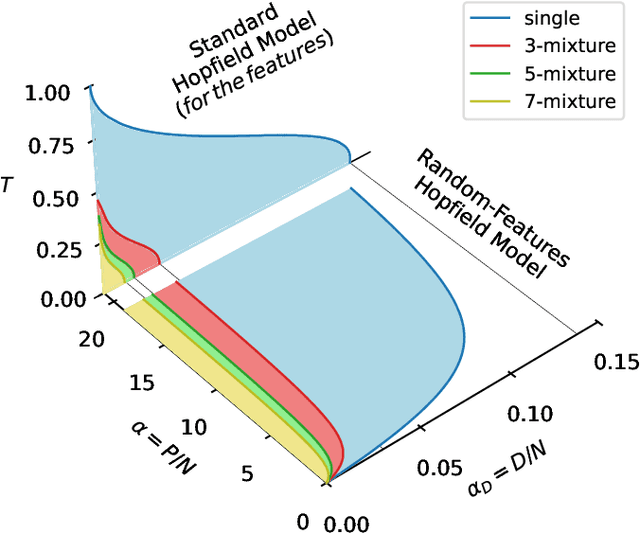
Abstract:It has been recently shown that a learning transition happens when a Hopfield Network stores examples generated as superpositions of random features, where new attractors corresponding to such features appear in the model. In this work we reveal that the network also develops attractors corresponding to previously unseen examples generated with the same set of features. We explain this surprising behaviour in terms of spurious states of the learned features: we argue that, increasing the number of stored examples beyond the learning transition, the model also learns to mix the features to represent both stored and previously unseen examples. We support this claim with the computation of the phase diagram of the model.
The twin peaks of learning neural networks
Jan 23, 2024Abstract:Recent works demonstrated the existence of a double-descent phenomenon for the generalization error of neural networks, where highly overparameterized models escape overfitting and achieve good test performance, at odds with the standard bias-variance trade-off described by statistical learning theory. In the present work, we explore a link between this phenomenon and the increase of complexity and sensitivity of the function represented by neural networks. In particular, we study the Boolean mean dimension (BMD), a metric developed in the context of Boolean function analysis. Focusing on a simple teacher-student setting for the random feature model, we derive a theoretical analysis based on the replica method that yields an interpretable expression for the BMD, in the high dimensional regime where the number of data points, the number of features, and the input size grow to infinity. We find that, as the degree of overparameterization of the network is increased, the BMD reaches an evident peak at the interpolation threshold, in correspondence with the generalization error peak, and then slowly approaches a low asymptotic value. The same phenomenology is then traced in numerical experiments with different model classes and training setups. Moreover, we find empirically that adversarially initialized models tend to show higher BMD values, and that models that are more robust to adversarial attacks exhibit a lower BMD.
High-dimensional manifold of solutions in neural networks: insights from statistical physics
Sep 17, 2023Abstract:In these pedagogic notes I review the statistical mechanics approach to neural networks, focusing on the paradigmatic example of the perceptron architecture with binary an continuous weights, in the classification setting. I will review the Gardner's approach based on replica method and the derivation of the SAT/UNSAT transition in the storage setting. Then, I discuss some recent works that unveiled how the zero training error configurations are geometrically arranged, and how this arrangement changes as the size of the training set increases. I also illustrate how different regions of solution space can be explored analytically and how the landscape in the vicinity of a solution can be characterized. I give evidence how, in binary weight models, algorithmic hardness is a consequence of the disappearance of a clustered region of solutions that extends to very large distances. Finally, I demonstrate how the study of linear mode connectivity between solutions can give insights into the average shape of the solution manifold.
The star-shaped space of solutions of the spherical negative perceptron
May 18, 2023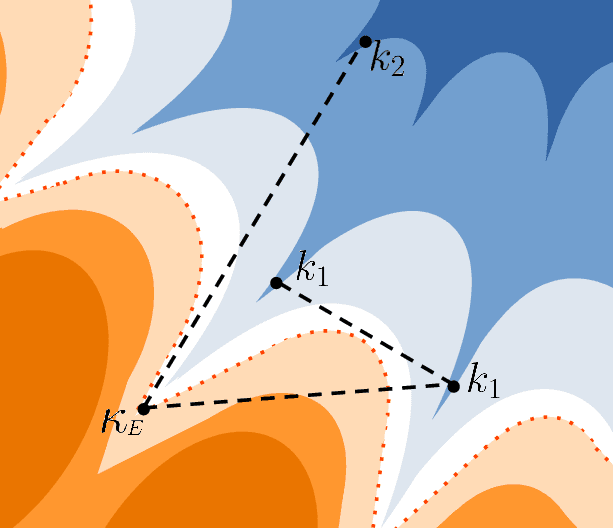
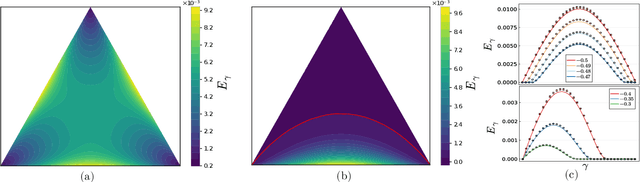
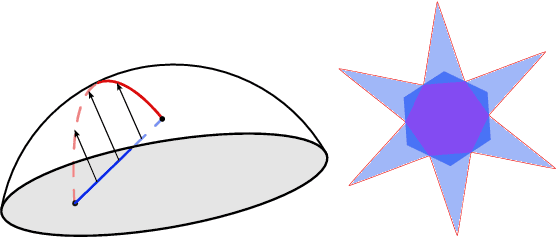
Abstract:Empirical studies on the landscape of neural networks have shown that low-energy configurations are often found in complex connected structures, where zero-energy paths between pairs of distant solutions can be constructed. Here we consider the spherical negative perceptron, a prototypical non-convex neural network model framed as a continuous constraint satisfaction problem. We introduce a general analytical method for computing energy barriers in the simplex with vertex configurations sampled from the equilibrium. We find that in the over-parameterized regime the solution manifold displays simple connectivity properties. There exists a large geodesically convex component that is attractive for a wide range of optimization dynamics. Inside this region we identify a subset of atypically robust solutions that are geodesically connected with most other solutions, giving rise to a star-shaped geometry. We analytically characterize the organization of the connected space of solutions and show numerical evidence of a transition, at larger constraint densities, where the aforementioned simple geodesic connectivity breaks down.
Typical and atypical solutions in non-convex neural networks with discrete and continuous weights
Apr 26, 2023Abstract:We study the binary and continuous negative-margin perceptrons as simple non-convex neural network models learning random rules and associations. We analyze the geometry of the landscape of solutions in both models and find important similarities and differences. Both models exhibit subdominant minimizers which are extremely flat and wide. These minimizers coexist with a background of dominant solutions which are composed by an exponential number of algorithmically inaccessible small clusters for the binary case (the frozen 1-RSB phase) or a hierarchical structure of clusters of different sizes for the spherical case (the full RSB phase). In both cases, when a certain threshold in constraint density is crossed, the local entropy of the wide flat minima becomes non-monotonic, indicating a break-up of the space of robust solutions into disconnected components. This has a strong impact on the behavior of algorithms in binary models, which cannot access the remaining isolated clusters. For the spherical case the behaviour is different, since even beyond the disappearance of the wide flat minima the remaining solutions are shown to always be surrounded by a large number of other solutions at any distance, up to capacity. Indeed, we exhibit numerical evidence that algorithms seem to find solutions up to the SAT/UNSAT transition, that we compute here using an 1RSB approximation. For both models, the generalization performance as a learning device is shown to be greatly improved by the existence of wide flat minimizers even when trained in the highly underconstrained regime of very negative margins.
Learning through atypical ''phase transitions'' in overparameterized neural networks
Oct 01, 2021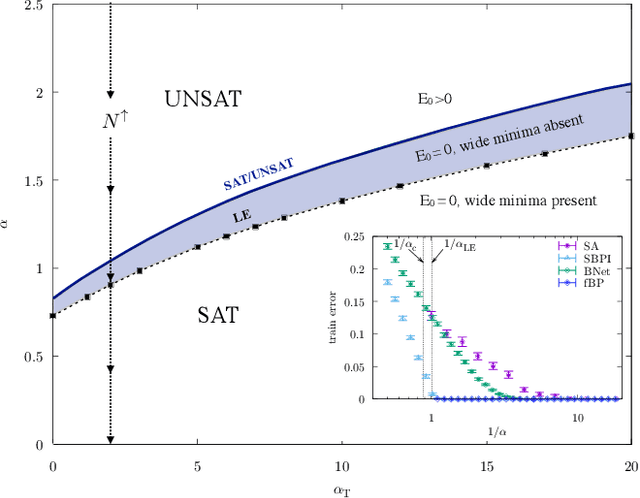
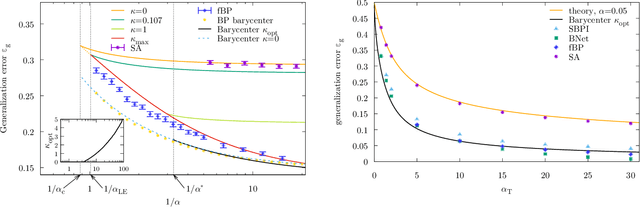

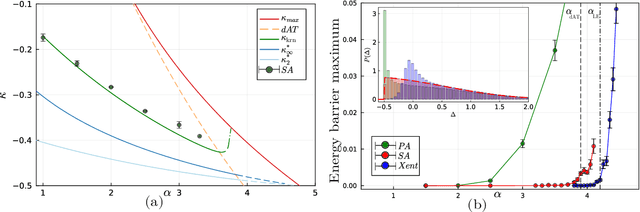
Abstract:Current deep neural networks are highly overparameterized (up to billions of connection weights) and nonlinear. Yet they can fit data almost perfectly through variants of gradient descent algorithms and achieve unexpected levels of prediction accuracy without overfitting. These are formidable results that escape the bias-variance predictions of statistical learning and pose conceptual challenges for non-convex optimization. In this paper, we use methods from statistical physics of disordered systems to analytically study the computational fallout of overparameterization in nonconvex neural network models. As the number of connection weights increases, we follow the changes of the geometrical structure of different minima of the error loss function and relate them to learning and generalisation performance. We find that there exist a gap between the SAT/UNSAT interpolation transition where solutions begin to exist and the point where algorithms start to find solutions, i.e. where accessible solutions appear. This second phase transition coincides with the discontinuous appearance of atypical solutions that are locally extremely entropic, i.e., flat regions of the weight space that are particularly solution-dense and have good generalization properties. Although exponentially rare compared to typical solutions (which are narrower and extremely difficult to sample), entropic solutions are accessible to the algorithms used in learning. We can characterize the generalization error of different solutions and optimize the Bayesian prediction, for data generated from a structurally different network. Numerical tests on observables suggested by the theory confirm that the scenario extends to realistic deep networks.
Unveiling the structure of wide flat minima in neural networks
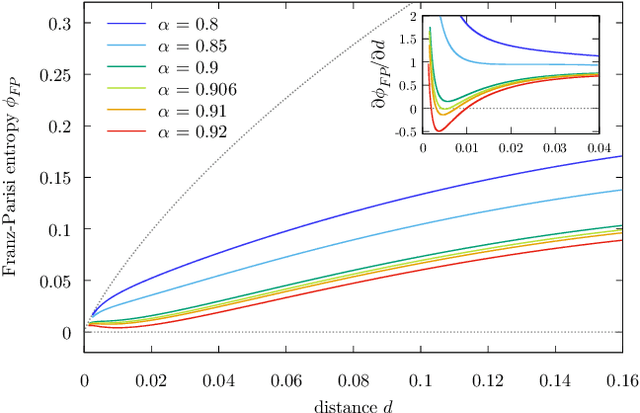
Jul 02, 2021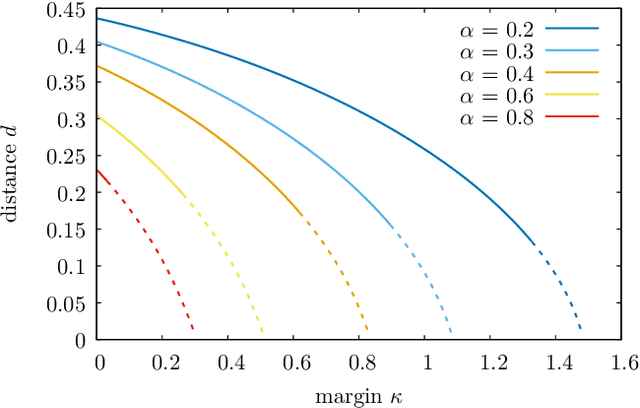
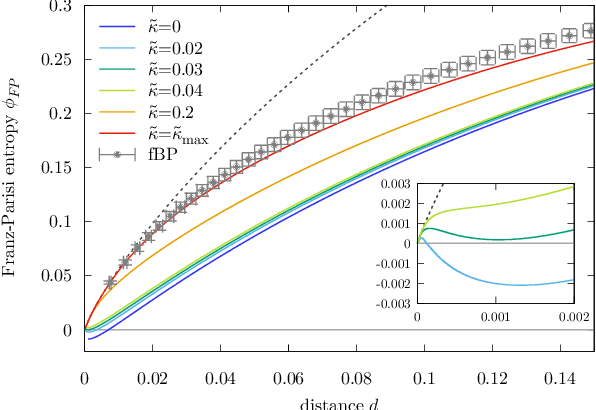
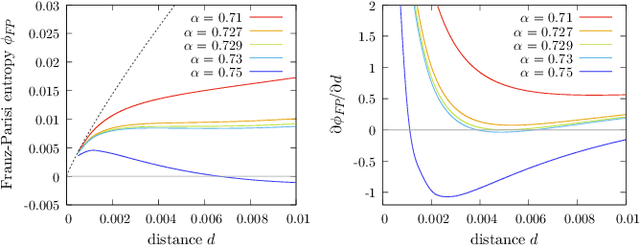
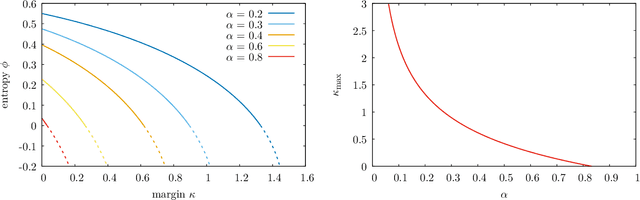
Abstract:The success of deep learning has revealed the application potential of neural networks across the sciences and opened up fundamental theoretical problems. In particular, the fact that learning algorithms based on simple variants of gradient methods are able to find near-optimal minima of highly nonconvex loss functions is an unexpected feature of neural networks which needs to be understood in depth. Such algorithms are able to fit the data almost perfectly, even in the presence of noise, and yet they have excellent predictive capabilities. Several empirical results have shown a reproducible correlation between the so-called flatness of the minima achieved by the algorithms and the generalization performance. At the same time, statistical physics results have shown that in nonconvex networks a multitude of narrow minima may coexist with a much smaller number of wide flat minima, which generalize well. Here we show that wide flat minima arise from the coalescence of minima that correspond to high-margin classifications. Despite being exponentially rare compared to zero-margin solutions, high-margin minima tend to concentrate in particular regions. These minima are in turn surrounded by other solutions of smaller and smaller margin, leading to dense regions of solutions over long distances. Our analysis also provides an alternative analytical method for estimating when flat minima appear and when algorithms begin to find solutions, as the number of model parameters varies.
Wide flat minima and optimal generalization in classifying high-dimensional Gaussian mixtures
Oct 27, 2020



Abstract:We analyze the connection between minimizers with good generalizing properties and high local entropy regions of a threshold-linear classifier in Gaussian mixtures with the mean squared error loss function. We show that there exist configurations that achieve the Bayes-optimal generalization error, even in the case of unbalanced clusters. We explore analytically the error-counting loss landscape in the vicinity of a Bayes-optimal solution, and show that the closer we get to such configurations, the higher the local entropy, implying that the Bayes-optimal solution lays inside a wide flat region. We also consider the algorithmically relevant case of targeting wide flat minima of the (differentiable) mean squared error loss. Our analytical and numerical results show not only that in the balanced case the dependence on the norm of the weights is mild, but also, in the unbalanced case, that the performances can be improved.
Entropic gradient descent algorithms and wide flat minima
Jun 14, 2020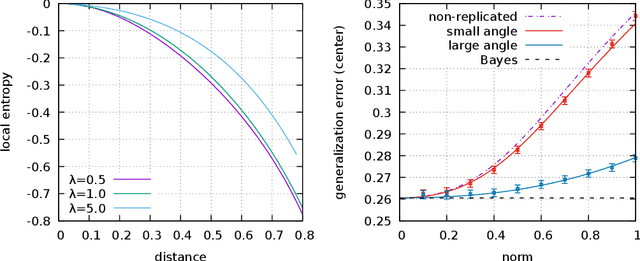
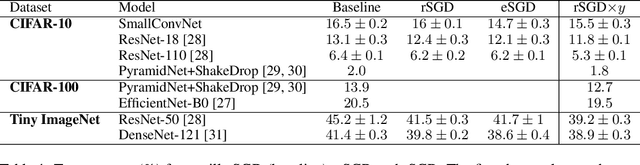

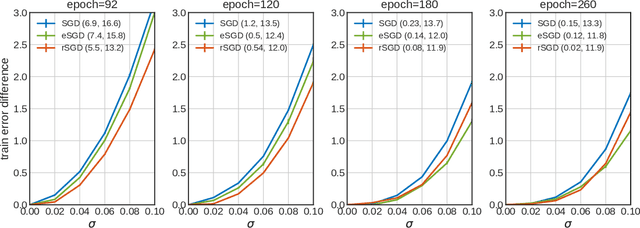
Abstract:The properties of flat minima in the empirical risk landscape of neural networks have been debated for some time. Increasing evidence suggests they possess better generalization capabilities with respect to sharp ones. First, we discuss Gaussian mixture classification models and show analytically that there exist Bayes optimal pointwise estimators which correspond to minimizers belonging to wide flat regions. These estimators can be found by applying maximum flatness algorithms either directly on the classifier (which is norm independent) or on the differentiable loss function used in learning. Next, we extend the analysis to the deep learning scenario by extensive numerical validations. Using two algorithms, Entropy-SGD and Replicated-SGD, that explicitly include in the optimization objective a non-local flatness measure known as local entropy, we consistently improve the generalization error for common architectures (e.g. ResNet, EfficientNet). An easy to compute flatness measure shows a clear correlation with test accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge