Voxtral TTS

We introduce Voxtral TTS, an expressive multilingual text-to-speech model that generates natural speech from as little as 3 seconds of reference audio. Voxtral TTS adopts a hybrid architecture that combines auto-regressive generation of semantic speech tokens with flow-matching for acoustic tokens. These tokens are encoded and decoded with Voxtral Codec, a speech tokenizer trained from scratch with a hybrid VQ-FSQ quantization scheme. In human evaluations conducted by native speakers, Voxtral TTS is preferred for multilingual voice cloning due to its naturalness and expressivity, achieving a 68.4\% win rate over ElevenLabs Flash v2.5. We release the model weights under a CC BY-NC license.

Sampling through Algorithmic Diffusion in non-convex Perceptron problems

We analyze the problem of sampling from the solution space of simple yet non-convex neural network models by employing a denoising diffusion process known as Algorithmic Stochastic Localization, where the score function is provided by Approximate Message Passing. We introduce a formalism based on the replica method to characterize the process in the infinite-size limit in terms of a few order parameters, and, in particular, we provide criteria for the feasibility of sampling. We show that, in the case of the spherical perceptron problem with negative stability, approximate uniform sampling is achievable across the entire replica symmetric region of the phase diagram. In contrast, for the binary perceptron, uniform sampling via diffusion invariably fails due to the overlap gap property exhibited by the typical set of solutions. We discuss the first steps in defining alternative measures that can be efficiently sampled.

The twin peaks of learning neural networks

Recent works demonstrated the existence of a double-descent phenomenon for the generalization error of neural networks, where highly overparameterized models escape overfitting and achieve good test performance, at odds with the standard bias-variance trade-off described by statistical learning theory. In the present work, we explore a link between this phenomenon and the increase of complexity and sensitivity of the function represented by neural networks. In particular, we study the Boolean mean dimension (BMD), a metric developed in the context of Boolean function analysis. Focusing on a simple teacher-student setting for the random feature model, we derive a theoretical analysis based on the replica method that yields an interpretable expression for the BMD, in the high dimensional regime where the number of data points, the number of features, and the input size grow to infinity. We find that, as the degree of overparameterization of the network is increased, the BMD reaches an evident peak at the interpolation threshold, in correspondence with the generalization error peak, and then slowly approaches a low asymptotic value. The same phenomenology is then traced in numerical experiments with different model classes and training setups. Moreover, we find empirically that adversarially initialized models tend to show higher BMD values, and that models that are more robust to adversarial attacks exhibit a lower BMD.

Entropic gradient descent algorithms and wide flat minima

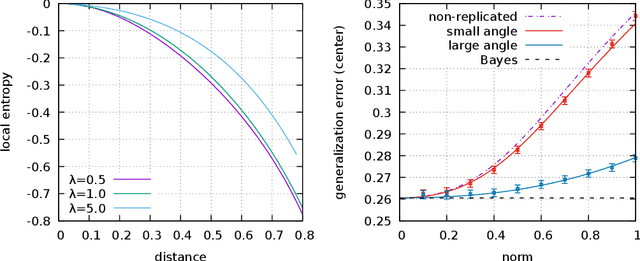
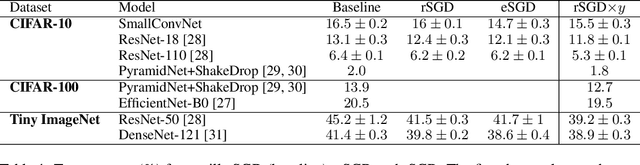
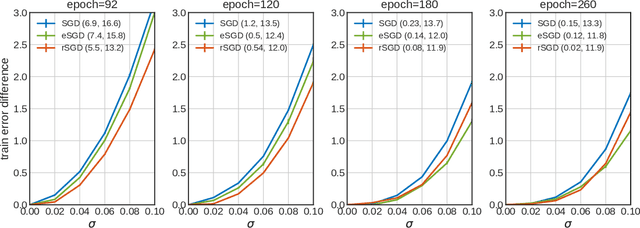
The properties of flat minima in the empirical risk landscape of neural networks have been debated for some time. Increasing evidence suggests they possess better generalization capabilities with respect to sharp ones. First, we discuss Gaussian mixture classification models and show analytically that there exist Bayes optimal pointwise estimators which correspond to minimizers belonging to wide flat regions. These estimators can be found by applying maximum flatness algorithms either directly on the classifier (which is norm independent) or on the differentiable loss function used in learning. Next, we extend the analysis to the deep learning scenario by extensive numerical validations. Using two algorithms, Entropy-SGD and Replicated-SGD, that explicitly include in the optimization objective a non-local flatness measure known as local entropy, we consistently improve the generalization error for common architectures (e.g. ResNet, EfficientNet). An easy to compute flatness measure shows a clear correlation with test accuracy.