Fabrizio Pittorino
SQUAD: Scalable Quorum Adaptive Decisions via ensemble of early exit neural networks
Jan 30, 2026Abstract:Early-exit neural networks have become popular for reducing inference latency by allowing intermediate predictions when sufficient confidence is achieved. However, standard approaches typically rely on single-model confidence thresholds, which are frequently unreliable due to inherent calibration issues. To address this, we introduce SQUAD (Scalable Quorum Adaptive Decisions), the first inference scheme that integrates early-exit mechanisms with distributed ensemble learning, improving uncertainty estimation while reducing the inference time. Unlike traditional methods that depend on individual confidence scores, SQUAD employs a quorum-based stopping criterion on early-exit learners by collecting intermediate predictions incrementally in order of computational complexity until a consensus is reached and halting the computation at that exit if the consensus is statistically significant. To maximize the efficacy of this voting mechanism, we also introduce QUEST (Quorum Search Technique), a Neural Architecture Search method to select early-exit learners with optimized hierarchical diversity, ensuring learners are complementary at every intermediate layer. This consensus-driven approach yields statistically robust early exits, improving the test accuracy up to 5.95% compared to state-of-the-art dynamic solutions with a comparable computational cost and reducing the inference latency up to 70.60% compared to static ensembles while maintaining a good accuracy.
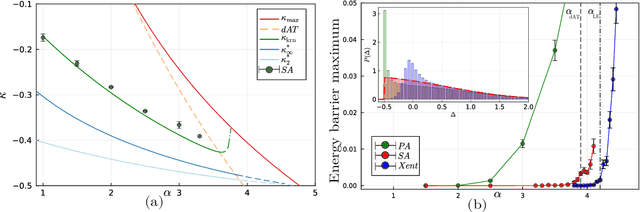
Architecture-Aware Minimization (A$^2$M): How to Find Flat Minima in Neural Architecture Search
Mar 13, 2025Abstract:Neural Architecture Search (NAS) has become an essential tool for designing effective and efficient neural networks. In this paper, we investigate the geometric properties of neural architecture spaces commonly used in differentiable NAS methods, specifically NAS-Bench-201 and DARTS. By defining flatness metrics such as neighborhoods and loss barriers along paths in architecture space, we reveal locality and flatness characteristics analogous to the well-known properties of neural network loss landscapes in weight space. In particular, we find that highly accurate architectures cluster together in flat regions, while suboptimal architectures remain isolated, unveiling the detailed geometrical structure of the architecture search landscape. Building on these insights, we propose Architecture-Aware Minimization (A$^2$M), a novel analytically derived algorithmic framework that explicitly biases, for the first time, the gradient of differentiable NAS methods towards flat minima in architecture space. A$^2$M consistently improves generalization over state-of-the-art DARTS-based algorithms on benchmark datasets including CIFAR-10, CIFAR-100, and ImageNet16-120, across both NAS-Bench-201 and DARTS search spaces. Notably, A$^2$M is able to increase the test accuracy, on average across different differentiable NAS methods, by +3.60\% on CIFAR-10, +4.60\% on CIFAR-100, and +3.64\% on ImageNet16-120, demonstrating its superior effectiveness in practice. A$^2$M can be easily integrated into existing differentiable NAS frameworks, offering a versatile tool for future research and applications in automated machine learning. We open-source our code at https://github.com/AI-Tech-Research-Lab/AsquaredM.
Quantifying Cryptocurrency Unpredictability: A Comprehensive Study of Complexity and Forecasting
Feb 13, 2025Abstract:This paper offers a thorough examination of the univariate predictability in cryptocurrency time-series. By exploiting a combination of complexity measure and model predictions we explore the cryptocurrencies time-series forecasting task focusing on the exchange rate in USD of Litecoin, Binance Coin, Bitcoin, Ethereum, and XRP. On one hand, to assess the complexity and the randomness of these time-series, a comparative analysis has been performed using Brownian and colored noises as a benchmark. The results obtained from the Complexity-Entropy causality plane and power density spectrum analysis reveal that cryptocurrency time-series exhibit characteristics closely resembling those of Brownian noise when analyzed in a univariate context. On the other hand, the application of a wide range of statistical, machine and deep learning models for time-series forecasting demonstrates the low predictability of cryptocurrencies. Notably, our analysis reveals that simpler models such as Naive models consistently outperform the more complex machine and deep learning ones in terms of forecasting accuracy across different forecast horizons and time windows. The combined study of complexity and forecasting accuracies highlights the difficulty of predicting the cryptocurrency market. These findings provide valuable insights into the inherent characteristics of the cryptocurrency data and highlight the need to reassess the challenges associated with predicting cryptocurrency's price movements.
* This is the author's accepted manuscript, modified per ACM self-archiving policy. The definitive Version of Record is available at https://doi.org/10.1145/3703412.3703420
Training Multi-Layer Binary Neural Networks With Local Binary Error Signals
Nov 28, 2024Abstract:Binary Neural Networks (BNNs) hold the potential for significantly reducing computational complexity and memory demand in machine and deep learning. However, most successful training algorithms for BNNs rely on quantization-aware floating-point Stochastic Gradient Descent (SGD), with full-precision hidden weights used during training. The binarized weights are only used at inference time, hindering the full exploitation of binary operations during the training process. In contrast to the existing literature, we introduce, for the first time, a multi-layer training algorithm for BNNs that does not require the computation of back-propagated full-precision gradients. Specifically, the proposed algorithm is based on local binary error signals and binary weight updates, employing integer-valued hidden weights that serve as a synaptic metaplasticity mechanism, thereby establishing it as a neurobiologically plausible algorithm. The binary-native and gradient-free algorithm proposed in this paper is capable of training binary multi-layer perceptrons (BMLPs) with binary inputs, weights, and activations, by using exclusively XNOR, Popcount, and increment/decrement operations, hence effectively paving the way for a new class of operation-optimized training algorithms. Experimental results on BMLPs fully trained in a binary-native and gradient-free manner on multi-class image classification benchmarks demonstrate an accuracy improvement of up to +13.36% compared to the fully binary state-of-the-art solution, showing minimal accuracy degradation compared to the same architecture trained with full-precision SGD and floating-point weights, activations, and inputs. The proposed algorithm is made available to the scientific community as a public repository.
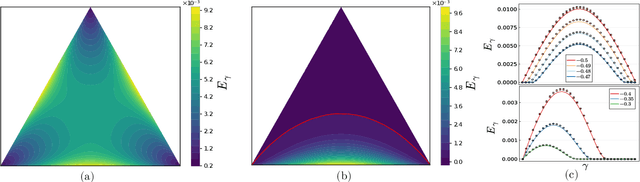
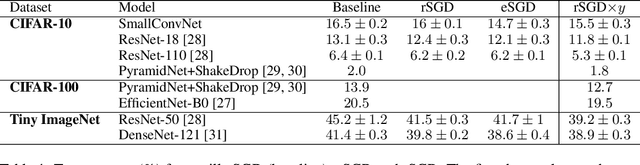
FlatNAS: optimizing Flatness in Neural Architecture Search for Out-of-Distribution Robustness
Feb 29, 2024Abstract:Neural Architecture Search (NAS) paves the way for the automatic definition of Neural Network (NN) architectures, attracting increasing research attention and offering solutions in various scenarios. This study introduces a novel NAS solution, called Flat Neural Architecture Search (FlatNAS), which explores the interplay between a novel figure of merit based on robustness to weight perturbations and single NN optimization with Sharpness-Aware Minimization (SAM). FlatNAS is the first work in the literature to systematically explore flat regions in the loss landscape of NNs in a NAS procedure, while jointly optimizing their performance on in-distribution data, their out-of-distribution (OOD) robustness, and constraining the number of parameters in their architecture. Differently from current studies primarily concentrating on OOD algorithms, FlatNAS successfully evaluates the impact of NN architectures on OOD robustness, a crucial aspect in real-world applications of machine and deep learning. FlatNAS achieves a good trade-off between performance, OOD generalization, and the number of parameters, by using only in-distribution data in the NAS exploration. The OOD robustness of the NAS-designed models is evaluated by focusing on robustness to input data corruptions, using popular benchmark datasets in the literature.
The star-shaped space of solutions of the spherical negative perceptron
May 18, 2023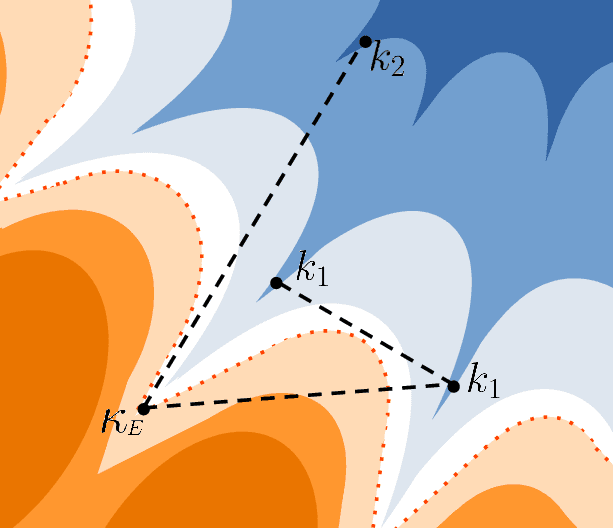
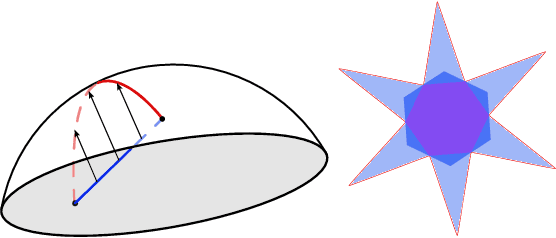
Abstract:Empirical studies on the landscape of neural networks have shown that low-energy configurations are often found in complex connected structures, where zero-energy paths between pairs of distant solutions can be constructed. Here we consider the spherical negative perceptron, a prototypical non-convex neural network model framed as a continuous constraint satisfaction problem. We introduce a general analytical method for computing energy barriers in the simplex with vertex configurations sampled from the equilibrium. We find that in the over-parameterized regime the solution manifold displays simple connectivity properties. There exists a large geodesically convex component that is attractive for a wide range of optimization dynamics. Inside this region we identify a subset of atypically robust solutions that are geodesically connected with most other solutions, giving rise to a star-shaped geometry. We analytically characterize the organization of the connected space of solutions and show numerical evidence of a transition, at larger constraint densities, where the aforementioned simple geodesic connectivity breaks down.
Deep Networks on Toroids: Removing Symmetries Reveals the Structure of Flat Regions in the Landscape Geometry
Feb 07, 2022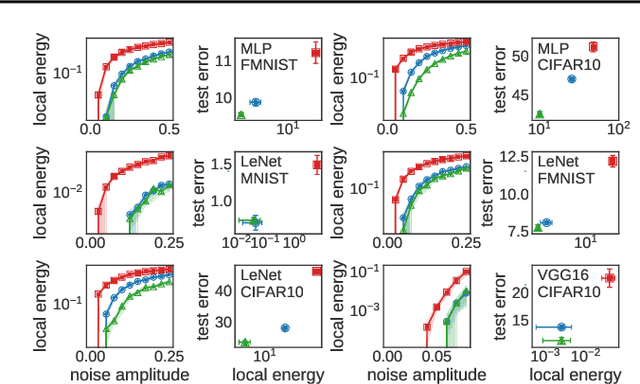
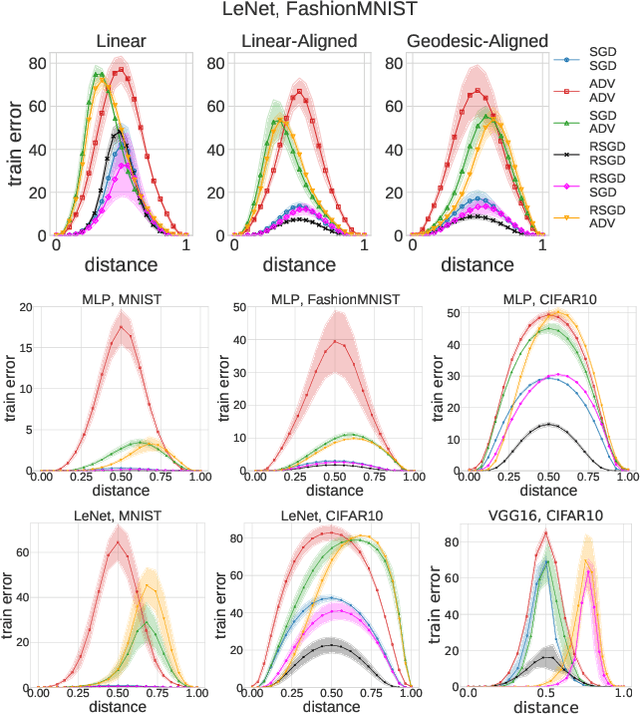
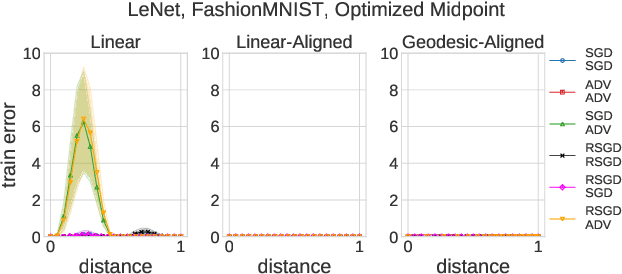
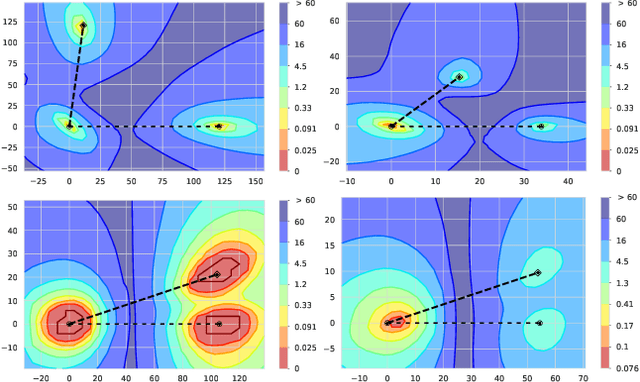
Abstract:We systematize the approach to the investigation of deep neural network landscapes by basing it on the geometry of the space of implemented functions rather than the space of parameters. Grouping classifiers into equivalence classes, we develop a standardized parameterization in which all symmetries are removed, resulting in a toroidal topology. On this space, we explore the error landscape rather than the loss. This lets us derive a meaningful notion of the flatness of minimizers and of the geodesic paths connecting them. Using different optimization algorithms that sample minimizers with different flatness we study the mode connectivity and other characteristics. Testing a variety of state-of-the-art architectures and benchmark datasets, we confirm the correlation between flatness and generalization performance; we further show that in function space flatter minima are closer to each other and that the barriers along the geodesics connecting them are small. We also find that minimizers found by variants of gradient descent can be connected by zero-error paths with a single bend. We observe similar qualitative results in neural networks with binary weights and activations, providing one of the first results concerning the connectivity in this setting. Our results hinge on symmetry removal, and are in remarkable agreement with the rich phenomenology described by some recent analytical studies performed on simple shallow models.
Deep learning via message passing algorithms based on belief propagation
Oct 27, 2021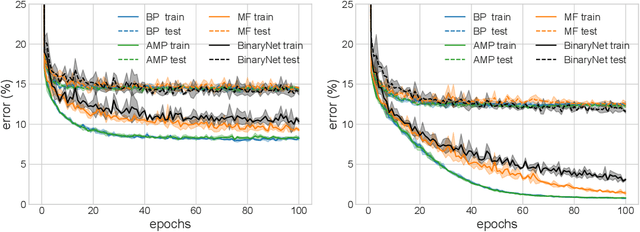

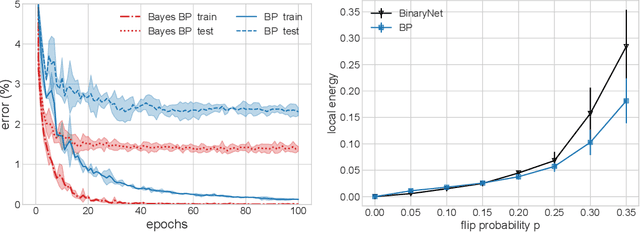

Abstract:Message-passing algorithms based on the Belief Propagation (BP) equations constitute a well-known distributed computational scheme. It is exact on tree-like graphical models and has also proven to be effective in many problems defined on graphs with loops (from inference to optimization, from signal processing to clustering). The BP-based scheme is fundamentally different from stochastic gradient descent (SGD), on which the current success of deep networks is based. In this paper, we present and adapt to mini-batch training on GPUs a family of BP-based message-passing algorithms with a reinforcement field that biases distributions towards locally entropic solutions. These algorithms are capable of training multi-layer neural networks with discrete weights and activations with performance comparable to SGD-inspired heuristics (BinaryNet) and are naturally well-adapted to continual learning. Furthermore, using these algorithms to estimate the marginals of the weights allows us to make approximate Bayesian predictions that have higher accuracy than point-wise solutions.
Entropic gradient descent algorithms and wide flat minima
Jun 14, 2020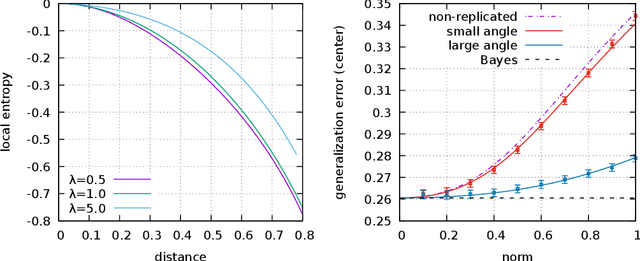

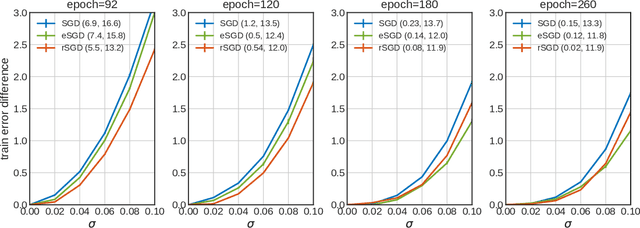
Abstract:The properties of flat minima in the empirical risk landscape of neural networks have been debated for some time. Increasing evidence suggests they possess better generalization capabilities with respect to sharp ones. First, we discuss Gaussian mixture classification models and show analytically that there exist Bayes optimal pointwise estimators which correspond to minimizers belonging to wide flat regions. These estimators can be found by applying maximum flatness algorithms either directly on the classifier (which is norm independent) or on the differentiable loss function used in learning. Next, we extend the analysis to the deep learning scenario by extensive numerical validations. Using two algorithms, Entropy-SGD and Replicated-SGD, that explicitly include in the optimization objective a non-local flatness measure known as local entropy, we consistently improve the generalization error for common architectures (e.g. ResNet, EfficientNet). An easy to compute flatness measure shows a clear correlation with test accuracy.
Shaping the learning landscape in neural networks around wide flat minima
May 21, 2019



Abstract:Learning in Deep Neural Networks (DNN) takes place by minimizing a non-convex high-dimensional loss function, typically by a stochastic gradient descent (SGD) strategy. The learning process is observed to be able to find good minimizers without getting stuck in local critical points, and that such minimizers are often satisfactory at avoiding overfitting. How these two features can be kept under control in nonlinear devices composed of millions of tunable connections is a profound and far reaching open question. In this paper we study basic non-convex neural network models which learn random patterns, and derive a number of basic geometrical and algorithmic features which suggest some answers. We first show that the error loss function presents few extremely wide flat minima (WFM) which coexist with narrower minima and critical points. We then show that the minimizers of the cross-entropy loss function overlap with the WFM of the error loss. We also show examples of learning devices for which WFM do not exist. From the algorithmic perspective we derive entropy driven greedy and message passing algorithms which focus their search on wide flat regions of minimizers. In the case of SGD and cross-entropy loss, we show that a slow reduction of the norm of the weights along the learning process also leads to WFM. We corroborate the results by a numerical study of the correlations between the volumes of the minimizers, their Hessian and their generalization performance on real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge