Brandon Livio Annesi
The star-shaped space of solutions of the spherical negative perceptron
May 18, 2023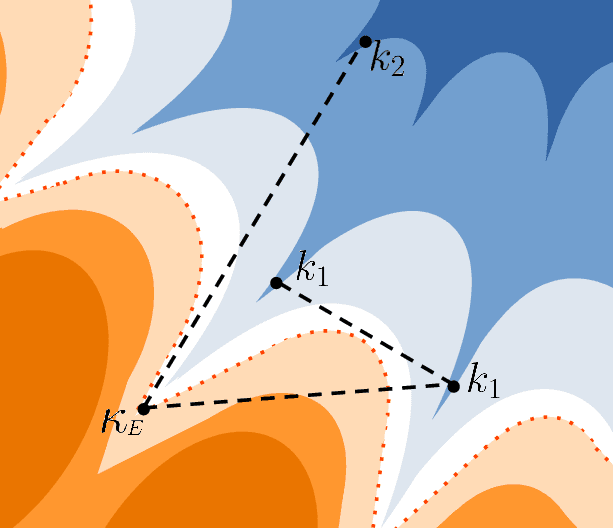
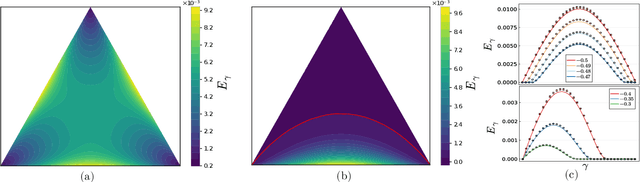
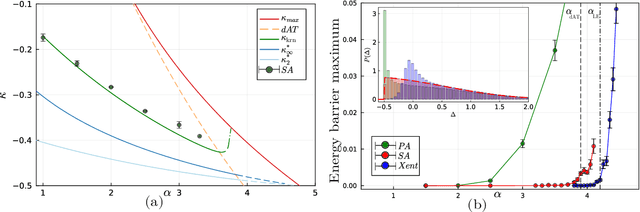
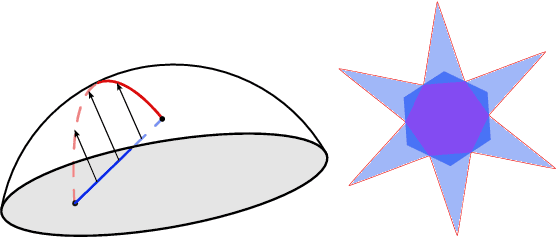
Abstract:Empirical studies on the landscape of neural networks have shown that low-energy configurations are often found in complex connected structures, where zero-energy paths between pairs of distant solutions can be constructed. Here we consider the spherical negative perceptron, a prototypical non-convex neural network model framed as a continuous constraint satisfaction problem. We introduce a general analytical method for computing energy barriers in the simplex with vertex configurations sampled from the equilibrium. We find that in the over-parameterized regime the solution manifold displays simple connectivity properties. There exists a large geodesically convex component that is attractive for a wide range of optimization dynamics. Inside this region we identify a subset of atypically robust solutions that are geodesically connected with most other solutions, giving rise to a star-shaped geometry. We analytically characterize the organization of the connected space of solutions and show numerical evidence of a transition, at larger constraint densities, where the aforementioned simple geodesic connectivity breaks down.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge