Random Features Hopfield Networks generalize retrieval to previously unseen examples
Paper and Code
Jul 08, 2024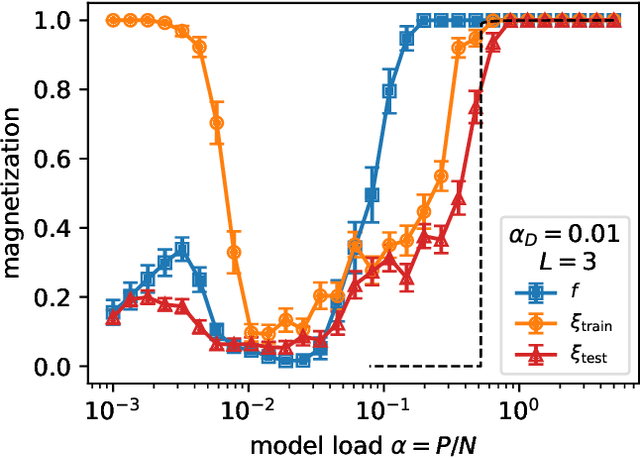
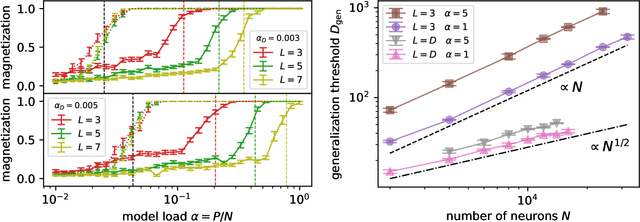
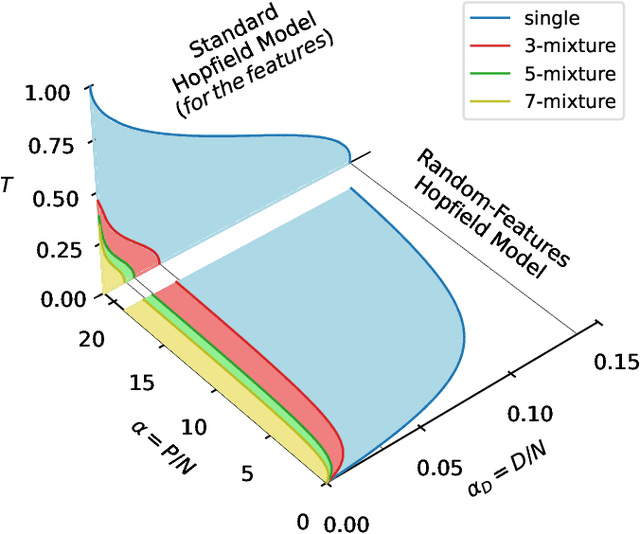
It has been recently shown that a learning transition happens when a Hopfield Network stores examples generated as superpositions of random features, where new attractors corresponding to such features appear in the model. In this work we reveal that the network also develops attractors corresponding to previously unseen examples generated with the same set of features. We explain this surprising behaviour in terms of spurious states of the learned features: we argue that, increasing the number of stored examples beyond the learning transition, the model also learns to mix the features to represent both stored and previously unseen examples. We support this claim with the computation of the phase diagram of the model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge