Kernel Renormalization in Bayesian Deep Neural Networks: the Equivalent Wishart Ansatz in the Proportional Regime

The scaling limit where both the size of the training set $P$ and the width $N$ of a deep neural network grow at the same rate, the so-called proportional-width regime, has been intensely studied for shallow, single-hidden-layer networks. However, extending these non-perturbative results from shallow architectures to deep non-linear networks has proven very challenging. Here we present an effective approximate approach to predict the generalization performance of Bayesian multi-layer perceptrons (MLPs) of fixed depth $L$ on arbitrary high-dimensional data. We propose an equivalent Wishart Ansatz to capture the dominant stochastic fluctuations of the hierarchical empirical kernels of MLPs. This allows us to perform a large deviation analysis for the partition function of MLPs in the proportional limit, expressed in terms of a renormalized NNGP kernel. In this description, even strong representation learning in the proportional limit is encoded in at most $L$ scalar order parameters, determined self-consistently. Extending the approach to convolutional architectures (CNNs), we identify a hierarchical local kernel renormalization mechanism, which allows to quantify more complex data-dependent transformations of the large-width kernel in CNNs due to finite-width effects. We test our effective theory against sampling experiments from the Bayesian posterior of finite deep neural networks with depths $L \sim O(10)$ and $P\sim O(10^3)$ on classic benchmark datasets, finding overall very good agreement together with two distinct types of systematic deviations.

Les Houches Lectures on Deep Learning at Large & Infinite Width

These lectures, presented at the 2022 Les Houches Summer School on Statistical Physics and Machine Learning, focus on the infinite-width limit and large-width regime of deep neural networks. Topics covered include various statistical and dynamical properties of these networks. In particular, the lecturers discuss properties of random deep neural networks; connections between trained deep neural networks, linear models, kernels, and Gaussian processes that arise in the infinite-width limit; and perturbative and non-perturbative treatments of large but finite-width networks, at initialization and after training.

Learning through atypical ''phase transitions'' in overparameterized neural networks

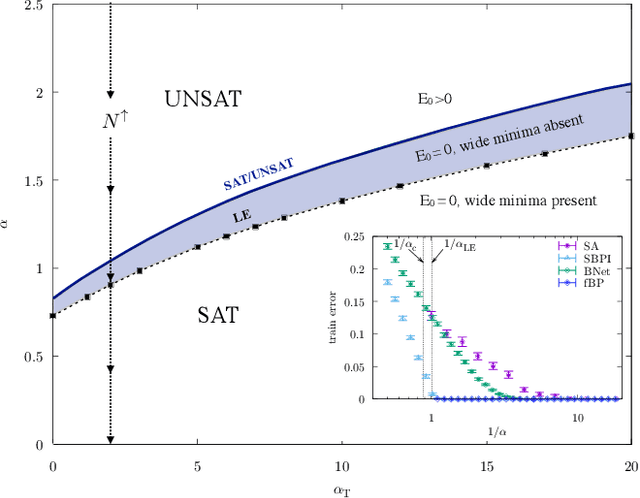
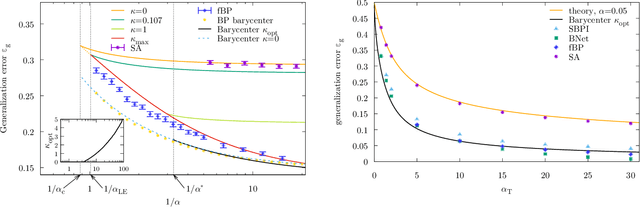
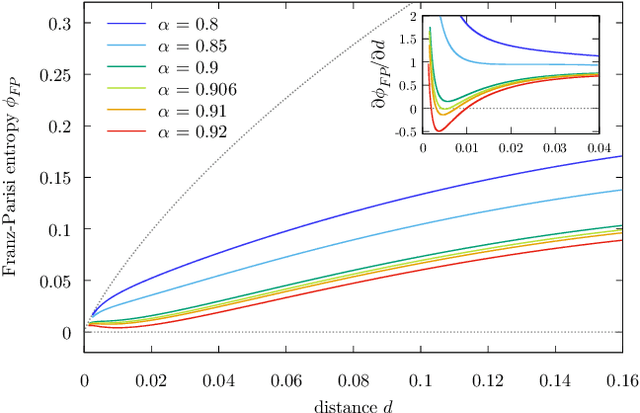
Current deep neural networks are highly overparameterized (up to billions of connection weights) and nonlinear. Yet they can fit data almost perfectly through variants of gradient descent algorithms and achieve unexpected levels of prediction accuracy without overfitting. These are formidable results that escape the bias-variance predictions of statistical learning and pose conceptual challenges for non-convex optimization. In this paper, we use methods from statistical physics of disordered systems to analytically study the computational fallout of overparameterization in nonconvex neural network models. As the number of connection weights increases, we follow the changes of the geometrical structure of different minima of the error loss function and relate them to learning and generalisation performance. We find that there exist a gap between the SAT/UNSAT interpolation transition where solutions begin to exist and the point where algorithms start to find solutions, i.e. where accessible solutions appear. This second phase transition coincides with the discontinuous appearance of atypical solutions that are locally extremely entropic, i.e., flat regions of the weight space that are particularly solution-dense and have good generalization properties. Although exponentially rare compared to typical solutions (which are narrower and extremely difficult to sample), entropic solutions are accessible to the algorithms used in learning. We can characterize the generalization error of different solutions and optimize the Bayesian prediction, for data generated from a structurally different network. Numerical tests on observables suggested by the theory confirm that the scenario extends to realistic deep networks.