Don't be lazy: CompleteP enables compute-efficient deep transformers

We study compute efficiency of LLM training when using different parameterizations, i.e., rules for adjusting model and optimizer hyperparameters (HPs) as model size changes. Some parameterizations fail to transfer optimal base HPs (such as learning rate) across changes in model depth, requiring practitioners to either re-tune these HPs as they scale up (expensive), or accept sub-optimal training when re-tuning is prohibitive. Even when they achieve HP transfer, we develop theory to show parameterizations may still exist in the lazy learning regime where layers learn only features close to their linearization, preventing effective use of depth and nonlinearity. Finally, we identify and adopt the unique parameterization we call CompleteP that achieves both depth-wise HP transfer and non-lazy learning in all layers. CompleteP enables a wider range of model width/depth ratios to remain compute-efficient, unlocking shapes better suited for different hardware settings and operational contexts. Moreover, CompleteP enables 12-34\% compute efficiency improvements over the prior state-of-the-art.

Deep Nets as Hamiltonians

Neural networks are complex functions of both their inputs and parameters. Much prior work in deep learning theory analyzes the distribution of network outputs at a fixed a set of inputs (e.g. a training dataset) over random initializations of the network parameters. The purpose of this article is to consider the opposite situation: we view a randomly initialized Multi-Layer Perceptron (MLP) as a Hamiltonian over its inputs. For typical realizations of the network parameters, we study the properties of the energy landscape induced by this Hamiltonian, focusing on the structure of near-global minimum in the limit of infinite width. Specifically, we use the replica trick to perform an exact analytic calculation giving the entropy (log volume of space) at a given energy. We further derive saddle point equations that describe the overlaps between inputs sampled iid from the Gibbs distribution induced by the random MLP. For linear activations we solve these saddle point equations exactly. But we also solve them numerically for a variety of depths and activation functions, including $\tanh, \sin, \text{ReLU}$, and shaped non-linearities. We find even at infinite width a rich range of behaviors. For some non-linearities, such as $\sin$, for instance, we find that the landscapes of random MLPs exhibit full replica symmetry breaking, while shallow $\tanh$ and ReLU networks or deep shaped MLPs are instead replica symmetric.

Optimizing Model Selection for Compound AI Systems

Compound AI systems that combine multiple LLM calls, such as self-refine and multi-agent-debate, achieve strong performance on many AI tasks. We address a core question in optimizing compound systems: for each LLM call or module in the system, how should one decide which LLM to use? We show that these LLM choices have a large effect on quality, but the search space is exponential. We propose LLMSelector, an efficient framework for model selection in compound systems, which leverages two key empirical insights: (i) end-to-end performance is often monotonic in how well each module performs, with all other modules held fixed, and (ii) per-module performance can be estimated accurately by an LLM. Building upon these insights, LLMSelector iteratively selects one module and allocates to it the model with the highest module-wise performance, as estimated by an LLM, until no further gain is possible. LLMSelector is applicable to any compound system with a bounded number of modules, and its number of API calls scales linearly with the number of modules, achieving high-quality model allocation both empirically and theoretically. Experiments with popular compound systems such as multi-agent debate and self-refine using LLMs such as GPT-4o, Claude 3.5 Sonnet and Gemini 1.5 show that LLMSelector confers 5%-70% accuracy gains compared to using the same LLM for all modules.

Unintentional Unalignment: Likelihood Displacement in Direct Preference Optimization

Direct Preference Optimization (DPO) and its variants are increasingly used for aligning language models with human preferences. Although these methods are designed to teach a model to generate preferred responses more frequently relative to dispreferred responses, prior work has observed that the likelihood of preferred responses often decreases during training. The current work sheds light on the causes and implications of this counter-intuitive phenomenon, which we term likelihood displacement. We demonstrate that likelihood displacement can be catastrophic, shifting probability mass from preferred responses to responses with an opposite meaning. As a simple example, training a model to prefer $\texttt{No}$ over $\texttt{Never}$ can sharply increase the probability of $\texttt{Yes}$. Moreover, when aligning the model to refuse unsafe prompts, we show that such displacement can unintentionally lead to unalignment, by shifting probability mass from preferred refusal responses to harmful responses (e.g., reducing the refusal rate of Llama-3-8B-Instruct from 74.4% to 33.4%). We theoretically characterize that likelihood displacement is driven by preferences that induce similar embeddings, as measured by a centered hidden embedding similarity (CHES) score. Empirically, the CHES score enables identifying which training samples contribute most to likelihood displacement in a given dataset. Filtering out these samples effectively mitigated unintentional unalignment in our experiments. More broadly, our results highlight the importance of curating data with sufficiently distinct preferences, for which we believe the CHES score may prove valuable.

Networks of Networks: Complexity Class Principles Applied to Compound AI Systems Design

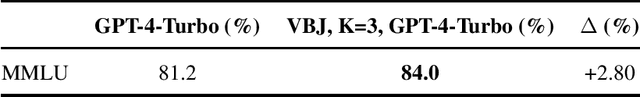
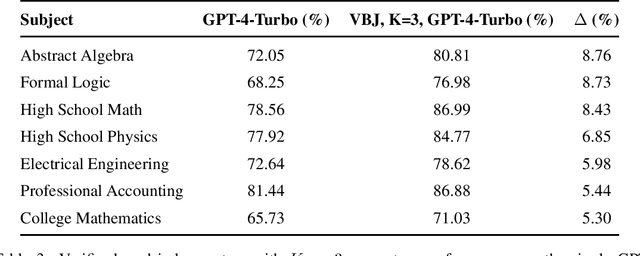
As practitioners seek to surpass the current reliability and quality frontier of monolithic models, Compound AI Systems consisting of many language model inference calls are increasingly employed. In this work, we construct systems, which we call Networks of Networks (NoNs) organized around the distinction between generating a proposed answer and verifying its correctness, a fundamental concept in complexity theory that we show empirically extends to Language Models (LMs). We introduce a verifier-based judge NoN with K generators, an instantiation of "best-of-K" or "judge-based" compound AI systems. Through experiments on synthetic tasks such as prime factorization, and core benchmarks such as the MMLU, we demonstrate notable performance gains. For instance, in factoring products of two 3-digit primes, a simple NoN improves accuracy from 3.7\% to 36.6\%. On MMLU, a verifier-based judge construction with only 3 generators boosts accuracy over individual GPT-4-Turbo calls by 2.8\%. Our analysis reveals that these gains are most pronounced in domains where verification is notably easier than generation--a characterization which we believe subsumes many reasoning and procedural knowledge tasks, but doesn't often hold for factual and declarative knowledge-based settings. For mathematical and formal logic reasoning-based subjects of MMLU, we observe a 5-8\% or higher gain, whilst no gain on others such as geography and religion. We provide key takeaways for ML practitioners, including the importance of considering verification complexity, the impact of witness format on verifiability, and a simple test to determine the potential benefit of this NoN approach for a given problem distribution. This work aims to inform future research and practice in the design of compound AI systems.

Bayesian Inference with Deep Weakly Nonlinear Networks

We show at a physics level of rigor that Bayesian inference with a fully connected neural network and a shaped nonlinearity of the form $\phi(t) = t + \psi t^3/L$ is (perturbatively) solvable in the regime where the number of training datapoints $P$ , the input dimension $N_0$, the network layer widths $N$, and the network depth $L$ are simultaneously large. Our results hold with weak assumptions on the data; the main constraint is that $P < N_0$. We provide techniques to compute the model evidence and posterior to arbitrary order in $1/N$ and at arbitrary temperature. We report the following results from the first-order computation: 1. When the width $N$ is much larger than the depth $L$ and training set size $P$, neural network Bayesian inference coincides with Bayesian inference using a kernel. The value of $\psi$ determines the curvature of a sphere, hyperbola, or plane into which the training data is implicitly embedded under the feature map. 2. When $LP/N$ is a small constant, neural network Bayesian inference departs from the kernel regime. At zero temperature, neural network Bayesian inference is equivalent to Bayesian inference using a data-dependent kernel, and $LP/N$ serves as an effective depth that controls the extent of feature learning. 3. In the restricted case of deep linear networks ($\psi=0$) and noisy data, we show a simple data model for which evidence and generalization error are optimal at zero temperature. As $LP/N$ increases, both evidence and generalization further improve, demonstrating the benefit of depth in benign overfitting.

Are More LLM Calls All You Need? Towards Scaling Laws of Compound Inference Systems

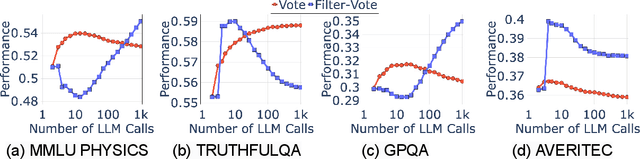
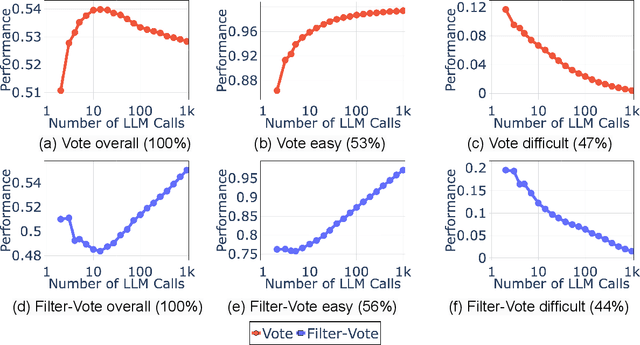
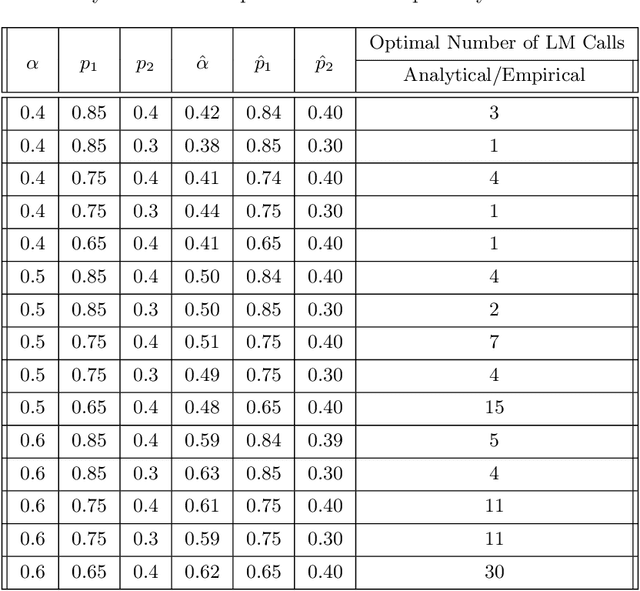
Many recent state-of-the-art results in language tasks were achieved using compound systems that perform multiple Large Language Model (LLM) calls and aggregate their responses. However, there is little understanding of how the number of LLM calls -- e.g., when asking the LLM to answer each question multiple times and taking a consensus -- affects such a compound system's performance. In this paper, we initiate the study of scaling laws of compound inference systems. We analyze, theoretically and empirically, how the number of LLM calls affects the performance of one-layer Voting Inference Systems -- one of the simplest compound systems, which aggregates LLM responses via majority voting. We find empirically that across multiple language tasks, surprisingly, Voting Inference Systems' performance first increases but then decreases as a function of the number of LLM calls. Our theoretical results suggest that this non-monotonicity is due to the diversity of query difficulties within a task: more LLM calls lead to higher performance on "easy" queries, but lower performance on "hard" queries, and non-monotone behavior emerges when a task contains both types of queries. This insight then allows us to compute, from a small number of samples, the number of LLM calls that maximizes system performance, and define a scaling law of Voting Inference Systems. Experiments show that our scaling law can predict the performance of Voting Inference Systems and find the optimal number of LLM calls to make.

Principled Architecture-aware Scaling of Hyperparameters

Training a high-quality deep neural network requires choosing suitable hyperparameters, which is a non-trivial and expensive process. Current works try to automatically optimize or design principles of hyperparameters, such that they can generalize to diverse unseen scenarios. However, most designs or optimization methods are agnostic to the choice of network structures, and thus largely ignore the impact of neural architectures on hyperparameters. In this work, we precisely characterize the dependence of initializations and maximal learning rates on the network architecture, which includes the network depth, width, convolutional kernel size, and connectivity patterns. By pursuing every parameter to be maximally updated with the same mean squared change in pre-activations, we can generalize our initialization and learning rates across MLPs (multi-layer perception) and CNNs (convolutional neural network) with sophisticated graph topologies. We verify our principles with comprehensive experiments. More importantly, our strategy further sheds light on advancing current benchmarks for architecture design. A fair comparison of AutoML algorithms requires accurate network rankings. However, we demonstrate that network rankings can be easily changed by better training networks in benchmarks with our architecture-aware learning rates and initialization.

Depthwise Hyperparameter Transfer in Residual Networks: Dynamics and Scaling Limit

The cost of hyperparameter tuning in deep learning has been rising with model sizes, prompting practitioners to find new tuning methods using a proxy of smaller networks. One such proposal uses $\mu$P parameterized networks, where the optimal hyperparameters for small width networks transfer to networks with arbitrarily large width. However, in this scheme, hyperparameters do not transfer across depths. As a remedy, we study residual networks with a residual branch scale of $1/\sqrt{\text{depth}}$ in combination with the $\mu$P parameterization. We provide experiments demonstrating that residual architectures including convolutional ResNets and Vision Transformers trained with this parameterization exhibit transfer of optimal hyperparameters across width and depth on CIFAR-10 and ImageNet. Furthermore, our empirical findings are supported and motivated by theory. Using recent developments in the dynamical mean field theory (DMFT) description of neural network learning dynamics, we show that this parameterization of ResNets admits a well-defined feature learning joint infinite-width and infinite-depth limit and show convergence of finite-size network dynamics towards this limit.

Les Houches Lectures on Deep Learning at Large & Infinite Width

These lectures, presented at the 2022 Les Houches Summer School on Statistical Physics and Machine Learning, focus on the infinite-width limit and large-width regime of deep neural networks. Topics covered include various statistical and dynamical properties of these networks. In particular, the lecturers discuss properties of random deep neural networks; connections between trained deep neural networks, linear models, kernels, and Gaussian processes that arise in the infinite-width limit; and perturbative and non-perturbative treatments of large but finite-width networks, at initialization and after training.