Are More LLM Calls All You Need? Towards Scaling Laws of Compound Inference Systems

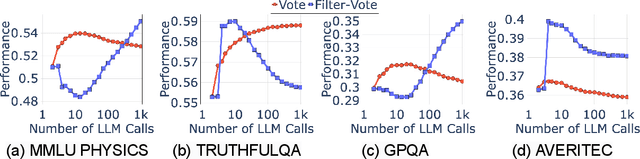
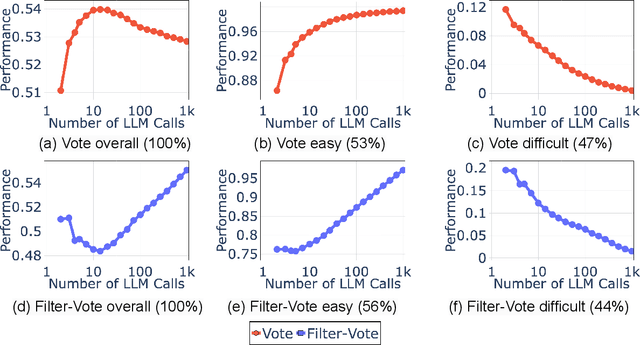
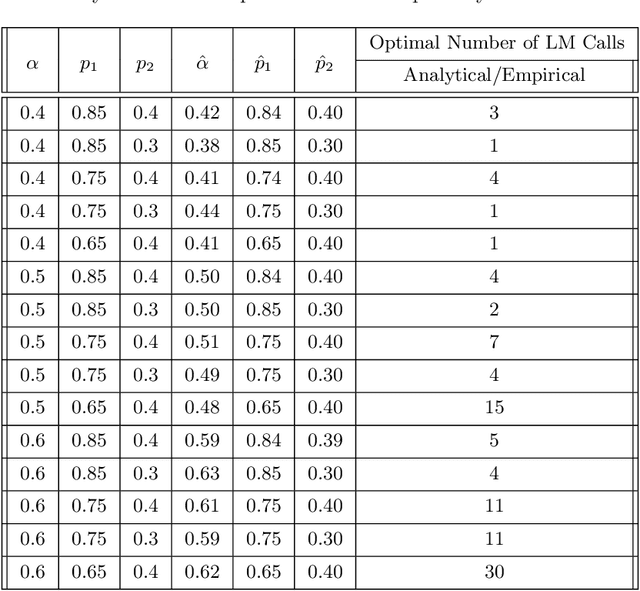
Many recent state-of-the-art results in language tasks were achieved using compound systems that perform multiple Large Language Model (LLM) calls and aggregate their responses. However, there is little understanding of how the number of LLM calls -- e.g., when asking the LLM to answer each question multiple times and taking a consensus -- affects such a compound system's performance. In this paper, we initiate the study of scaling laws of compound inference systems. We analyze, theoretically and empirically, how the number of LLM calls affects the performance of one-layer Voting Inference Systems -- one of the simplest compound systems, which aggregates LLM responses via majority voting. We find empirically that across multiple language tasks, surprisingly, Voting Inference Systems' performance first increases but then decreases as a function of the number of LLM calls. Our theoretical results suggest that this non-monotonicity is due to the diversity of query difficulties within a task: more LLM calls lead to higher performance on "easy" queries, but lower performance on "hard" queries, and non-monotone behavior emerges when a task contains both types of queries. This insight then allows us to compute, from a small number of samples, the number of LLM calls that maximizes system performance, and define a scaling law of Voting Inference Systems. Experiments show that our scaling law can predict the performance of Voting Inference Systems and find the optimal number of LLM calls to make.