Demystifying LLM-as-a-Judge: Analytically Tractable Model for Inference-Time Scaling

Recent developments in large language models have shown advantages in reallocating a notable share of computational resource from training time to inference time. However, the principles behind inference time scaling are not well understood. In this paper, we introduce an analytically tractable model of inference-time scaling: Bayesian linear regression with a reward-weighted sampler, where the reward is determined from a linear model, modeling LLM-as-a-judge scenario. We study this problem in the high-dimensional regime, where the deterministic equivalents dictate a closed-form expression for the posterior predictive mean and variance. We analyze the generalization error when training data are sampled from a teacher model. We draw $k$ inference-time samples and select via softmax at a temperature applied to a quadratic reward. When the reward is not too different from the teacher, the generalization error decreases monotonically with increasing inference time samples $k$. However, the specific reward that optimizes inference-time selection generally differs from the teacher. In contrast, substantial reward misspecification induces a finite optimal $k$ beyond which more sampling can increase the generalization error. For fixed $k$, there exists an optimal sampling temperature. We experimentally verify these facts in large language model inference with an additional large language model as a judge. In the "best-of-$k$" limit with the teacher as reward, we theoretically show that the generalization error decays as $Θ(1/k^2)$ and determine the leading coefficient via extreme value theory. These formulas delineate domains where scaling inference-time computation is provably preferable to collecting more data. Finally, we demonstrate that when task difficulty increases, the previously mentioned advantage of inference-time compute degrades.

Pretrain-Test Task Alignment Governs Generalization in In-Context Learning

In-context learning (ICL) is a central capability of Transformer models, but the structures in data that enable its emergence and govern its robustness remain poorly understood. In this work, we study how the structure of pretraining tasks governs generalization in ICL. Using a solvable model for ICL of linear regression by linear attention, we derive an exact expression for ICL generalization error in high dimensions under arbitrary pretraining-testing task covariance mismatch. This leads to a new alignment measure that quantifies how much information about the pretraining task distribution is useful for inference at test time. We show that this measure directly predicts ICL performance not only in the solvable model but also in nonlinear Transformers. Our analysis further reveals a tradeoff between specialization and generalization in ICL: depending on task distribution alignment, increasing pretraining task diversity can either improve or harm test performance. Together, these results identify train-test task alignment as a key determinant of generalization in ICL.

A Simplified Analysis of SGD for Linear Regression with Weight Averaging

Theoretically understanding stochastic gradient descent (SGD) in overparameterized models has led to the development of several optimization algorithms that are widely used in practice today. Recent work by~\citet{zou2021benign} provides sharp rates for SGD optimization in linear regression using constant learning rate, both with and without tail iterate averaging, based on a bias-variance decomposition of the risk. In our work, we provide a simplified analysis recovering the same bias and variance bounds provided in~\citep{zou2021benign} based on simple linear algebra tools, bypassing the requirement to manipulate operators on positive semi-definite (PSD) matrices. We believe our work makes the analysis of SGD on linear regression very accessible and will be helpful in further analyzing mini-batching and learning rate scheduling, leading to improvements in the training of realistic models.

Don't be lazy: CompleteP enables compute-efficient deep transformers

We study compute efficiency of LLM training when using different parameterizations, i.e., rules for adjusting model and optimizer hyperparameters (HPs) as model size changes. Some parameterizations fail to transfer optimal base HPs (such as learning rate) across changes in model depth, requiring practitioners to either re-tune these HPs as they scale up (expensive), or accept sub-optimal training when re-tuning is prohibitive. Even when they achieve HP transfer, we develop theory to show parameterizations may still exist in the lazy learning regime where layers learn only features close to their linearization, preventing effective use of depth and nonlinearity. Finally, we identify and adopt the unique parameterization we call CompleteP that achieves both depth-wise HP transfer and non-lazy learning in all layers. CompleteP enables a wider range of model width/depth ratios to remain compute-efficient, unlocking shapes better suited for different hardware settings and operational contexts. Moreover, CompleteP enables 12-34\% compute efficiency improvements over the prior state-of-the-art.

Error Broadcast and Decorrelation as a Potential Artificial and Natural Learning Mechanism

We introduce the Error Broadcast and Decorrelation (EBD) algorithm, a novel learning framework that addresses the credit assignment problem in neural networks by directly broadcasting output error to individual layers. Leveraging the stochastic orthogonality property of the optimal minimum mean square error (MMSE) estimator, EBD defines layerwise loss functions to penalize correlations between layer activations and output errors, offering a principled approach to error broadcasting without the need for weight transport. The optimization framework naturally leads to the experimentally observed three-factor learning rule and integrates with biologically plausible frameworks to enhance performance and plausibility. Numerical experiments demonstrate that EBD achieves performance comparable to or better than known error-broadcast methods on benchmark datasets. While the scalability of EBD to very large or complex datasets remains to be further explored, our findings suggest it provides a biologically plausible, efficient, and adaptable alternative for neural network training. This approach could inform future advancements in artificial and natural learning paradigms.

Echo Chamber: RL Post-training Amplifies Behaviors Learned in Pretraining

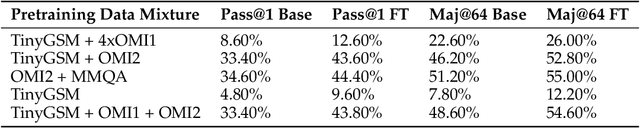
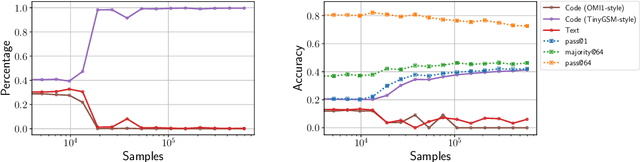
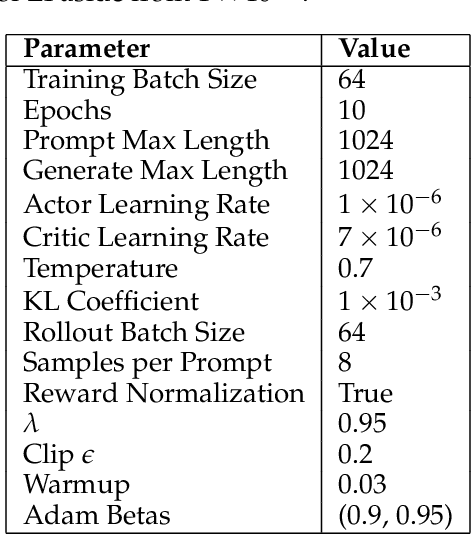
Reinforcement learning (RL)-based fine-tuning has become a crucial step in post-training language models for advanced mathematical reasoning and coding. Following the success of frontier reasoning models, recent work has demonstrated that RL fine-tuning consistently improves performance, even in smaller-scale models; however, the underlying mechanisms driving these improvements are not well-understood. Understanding the effects of RL fine-tuning requires disentangling its interaction with pretraining data composition, hyperparameters, and model scale, but such problems are exacerbated by the lack of transparency regarding the training data used in many existing models. In this work, we present a systematic end-to-end study of RL fine-tuning for mathematical reasoning by training models entirely from scratch on different mixtures of fully open datasets. We investigate the effects of various RL fine-tuning algorithms (PPO, GRPO, and Expert Iteration) across models of different scales. Our study reveals that RL algorithms consistently converge towards a dominant output distribution, amplifying patterns in the pretraining data. We also find that models of different scales trained on the same data mixture will converge to distinct output distributions, suggesting that there are scale-dependent biases in model generalization. Moreover, we find that RL post-training on simpler questions can lead to performance gains on harder ones, indicating that certain reasoning capabilities generalize across tasks. Our findings show that small-scale proxies in controlled settings can elicit interesting insights regarding the role of RL in shaping language model behavior.

Dynamically Learning to Integrate in Recurrent Neural Networks

Learning to remember over long timescales is fundamentally challenging for recurrent neural networks (RNNs). While much prior work has explored why RNNs struggle to learn long timescales and how to mitigate this, we still lack a clear understanding of the dynamics involved when RNNs learn long timescales via gradient descent. Here we build a mathematical theory of the learning dynamics of linear RNNs trained to integrate white noise. We show that when the initial recurrent weights are small, the dynamics of learning are described by a low-dimensional system that tracks a single outlier eigenvalue of the recurrent weights. This reveals the precise manner in which the long timescale associated with white noise integration is learned. We extend our analyses to RNNs learning a damped oscillatory filter, and find rich dynamical equations for the evolution of a conjugate pair of outlier eigenvalues. Taken together, our analyses build a rich mathematical framework for studying dynamical learning problems salient for both machine learning and neuroscience.

Learning richness modulates equality reasoning in neural networks

Equality reasoning is ubiquitous and purely abstract: sameness or difference may be evaluated no matter the nature of the underlying objects. As a result, same-different tasks (SD) have been extensively studied as a starting point for understanding abstract reasoning in humans and across animal species. With the rise of neural networks (NN) that exhibit striking apparent proficiency for abstractions, equality reasoning in NNs has also gained interest. Yet despite extensive study, conclusions about equality reasoning vary widely and with little consensus. To clarify the underlying principles in learning SD, we develop a theory of equality reasoning in multi-layer perceptrons (MLP). Following observations in comparative psychology, we propose a spectrum of behavior that ranges from conceptual to perceptual outcomes. Conceptual behavior is characterized by task-specific representations, efficient learning, and insensitivity to spurious perceptual details. Perceptual behavior is characterized by strong sensitivity to spurious perceptual details, accompanied by the need for exhaustive training to learn the task. We develop a mathematical theory to show that an MLP's behavior is driven by learning richness. Rich-regime MLPs exhibit conceptual behavior, whereas lazy-regime MLPs exhibit perceptual behavior. We validate our theoretical findings in vision SD experiments, showing that rich feature learning promotes success by encouraging hallmarks of conceptual behavior. Overall, our work identifies feature learning richness as a key parameter modulating equality reasoning, and suggests that equality reasoning in humans and animals may similarly depend on learning richness in neural circuits.

Adaptive kernel predictors from feature-learning infinite limits of neural networks

Previous influential work showed that infinite width limits of neural networks in the lazy training regime are described by kernel machines. Here, we show that neural networks trained in the rich, feature learning infinite-width regime in two different settings are also described by kernel machines, but with data-dependent kernels. For both cases, we provide explicit expressions for the kernel predictors and prescriptions to numerically calculate them. To derive the first predictor, we study the large-width limit of feature-learning Bayesian networks, showing how feature learning leads to task-relevant adaptation of layer kernels and preactivation densities. The saddle point equations governing this limit result in a min-max optimization problem that defines the kernel predictor. To derive the second predictor, we study gradient flow training of randomly initialized networks trained with weight decay in the infinite-width limit using dynamical mean field theory (DMFT). The fixed point equations of the arising DMFT defines the task-adapted internal representations and the kernel predictor. We compare our kernel predictors to kernels derived from lazy regime and demonstrate that our adaptive kernels achieve lower test loss on benchmark datasets.

Two-Point Deterministic Equivalence for Stochastic Gradient Dynamics in Linear Models

We derive a novel deterministic equivalence for the two-point function of a random matrix resolvent. Using this result, we give a unified derivation of the performance of a wide variety of high-dimensional linear models trained with stochastic gradient descent. This includes high-dimensional linear regression, kernel regression, and random feature models. Our results include previously known asymptotics as well as novel ones.