A Bayesian Perspective for Determinant Minimization Based Robust Structured Matrix Factorizatio

We introduce a Bayesian perspective for the structured matrix factorization problem. The proposed framework provides a probabilistic interpretation for existing geometric methods based on determinant minimization. We model input data vectors as linear transformations of latent vectors drawn from a distribution uniform over a particular domain reflecting structural assumptions, such as the probability simplex in Nonnegative Matrix Factorization and polytopes in Polytopic Matrix Factorization. We represent the rows of the linear transformation matrix as vectors generated independently from a normal distribution whose covariance matrix is inverse Wishart distributed. We show that the corresponding maximum a posteriori estimation problem boils down to the robust determinant minimization approach for structured matrix factorization, providing insights about parameter selections and potential algorithmic extensions.

Correlative Information Maximization Based Biologically Plausible Neural Networks for Correlated Source Separation

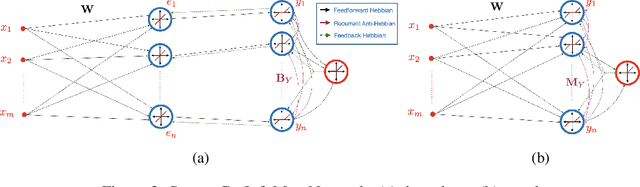
The brain effortlessly extracts latent causes of stimuli, but how it does this at the network level remains unknown. Most prior attempts at this problem proposed neural networks that implement independent component analysis which works under the limitation that latent causes are mutually independent. Here, we relax this limitation and propose a biologically plausible neural network that extracts correlated latent sources by exploiting information about their domains. To derive this network, we choose maximum correlative information transfer from inputs to outputs as the separation objective under the constraint that the outputs are restricted to their presumed sets. The online formulation of this optimization problem naturally leads to neural networks with local learning rules. Our framework incorporates infinitely many source domain choices and flexibly models complex latent structures. Choices of simplex or polytopic source domains result in networks with piecewise-linear activation functions. We provide numerical examples to demonstrate the superior correlated source separation capability for both synthetic and natural sources.

Biologically-Plausible Determinant Maximization Neural Networks for Blind Separation of Correlated Sources

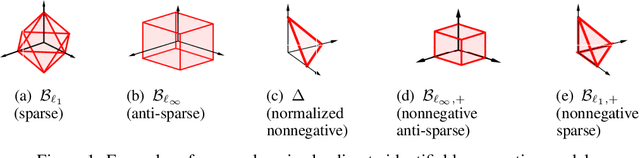
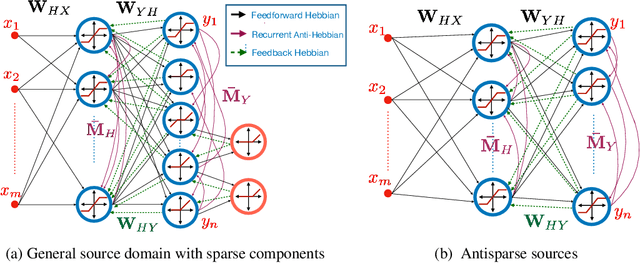
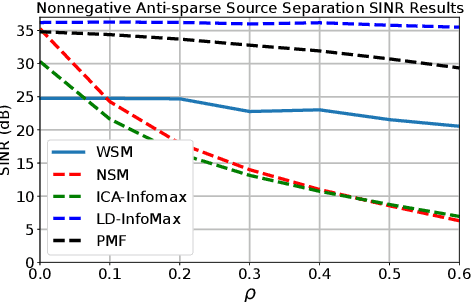
Extraction of latent sources of complex stimuli is critical for making sense of the world. While the brain solves this blind source separation (BSS) problem continuously, its algorithms remain unknown. Previous work on biologically-plausible BSS algorithms assumed that observed signals are linear mixtures of statistically independent or uncorrelated sources, limiting the domain of applicability of these algorithms. To overcome this limitation, we propose novel biologically-plausible neural networks for the blind separation of potentially dependent/correlated sources. Differing from previous work, we assume some general geometric, not statistical, conditions on the source vectors allowing separation of potentially dependent/correlated sources. Concretely, we assume that the source vectors are sufficiently scattered in their domains which can be described by certain polytopes. Then, we consider recovery of these sources by the Det-Max criterion, which maximizes the determinant of the output correlation matrix to enforce a similar spread for the source estimates. Starting from this normative principle, and using a weighted similarity matching approach that enables arbitrary linear transformations adaptable by local learning rules, we derive two-layer biologically-plausible neural network algorithms that can separate mixtures into sources coming from a variety of source domains. We demonstrate that our algorithms outperform other biologically-plausible BSS algorithms on correlated source separation problems.

Self-Supervised Learning with an Information Maximization Criterion

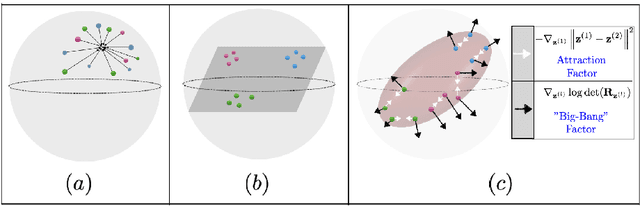
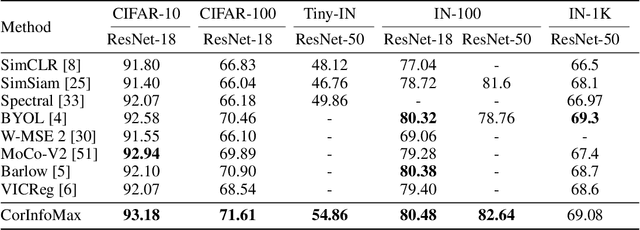
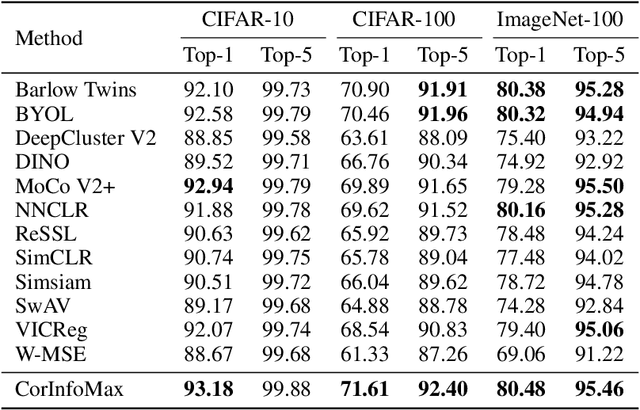
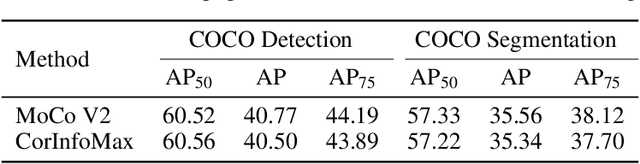
Self-supervised learning allows AI systems to learn effective representations from large amounts of data using tasks that do not require costly labeling. Mode collapse, i.e., the model producing identical representations for all inputs, is a central problem to many self-supervised learning approaches, making self-supervised tasks, such as matching distorted variants of the inputs, ineffective. In this article, we argue that a straightforward application of information maximization among alternative latent representations of the same input naturally solves the collapse problem and achieves competitive empirical results. We propose a self-supervised learning method, CorInfoMax, that uses a second-order statistics-based mutual information measure that reflects the level of correlation among its arguments. Maximizing this correlative information measure between alternative representations of the same input serves two purposes: (1) it avoids the collapse problem by generating feature vectors with non-degenerate covariances; (2) it establishes relevance among alternative representations by increasing the linear dependence among them. An approximation of the proposed information maximization objective simplifies to a Euclidean distance-based objective function regularized by the log-determinant of the feature covariance matrix. The regularization term acts as a natural barrier against feature space degeneracy. Consequently, beyond avoiding complete output collapse to a single point, the proposed approach also prevents dimensional collapse by encouraging the spread of information across the whole feature space. Numerical experiments demonstrate that CorInfoMax achieves better or competitive performance results relative to the state-of-the-art SSL approaches.

An Information Maximization Based Blind Source Separation Approach for Dependent and Independent Sources

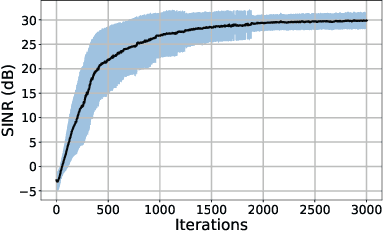
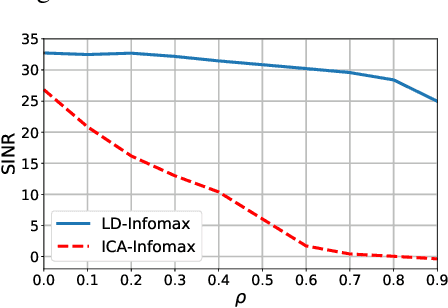
We introduce a new information maximization (infomax) approach for the blind source separation problem. The proposed framework provides an information-theoretic perspective for determinant maximization-based structured matrix factorization methods such as nonnegative and polytopic matrix factorization. For this purpose, we use an alternative joint entropy measure based on the log-determinant of covariance, which we refer to as log-determinant (LD) entropy. The corresponding (LD) mutual information between two vectors reflects a level of their correlation. We pose the infomax BSS criterion as the maximization of the LD-mutual information between the input and output of the separator under the constraint that the output vectors lie in a presumed domain set. In contrast to the ICA infomax approach, the proposed information maximization approach can separate both dependent and independent sources. Furthermore, we can provide a finite sample guarantee for the perfect separation condition in the noiseless case.

On Identifiable Polytope Characterization for Polytopic Matrix Factorization

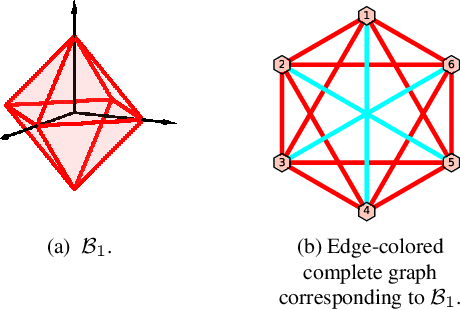
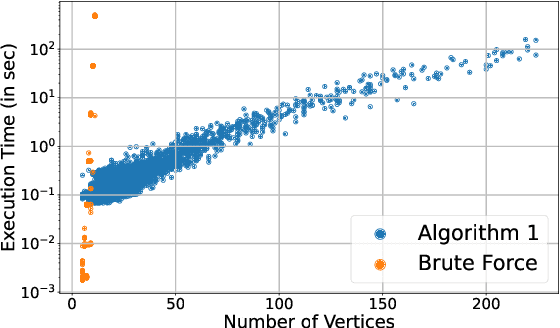
Polytopic matrix factorization (PMF) is a recently introduced matrix decomposition method in which the data vectors are modeled as linear transformations of samples from a polytope. The successful recovery of the original factors in the generative PMF model is conditioned on the "identifiability" of the chosen polytope. In this article, we investigate the problem of determining the identifiability of a polytope. The identifiability condition requires the polytope to be permutation-and/or-sign-only invariant. We show how this problem can be efficiently solved by using a graph automorphism algorithm. In particular, we show that checking only the generating set of the linear automorphism group of a polytope, which corresponds to the automorphism group of an edge-colored complete graph, is sufficient. This property prevents checking all the elements of the permutation group, which requires factorial algorithm complexity. We demonstrate the feasibility of the proposed approach through some numerical experiments.

Polytopic Matrix Factorization: Determinant Maximization Based Criterion and Identifiability

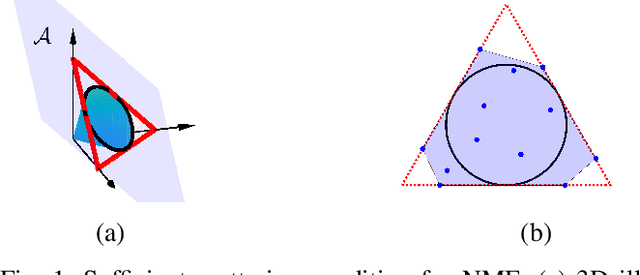
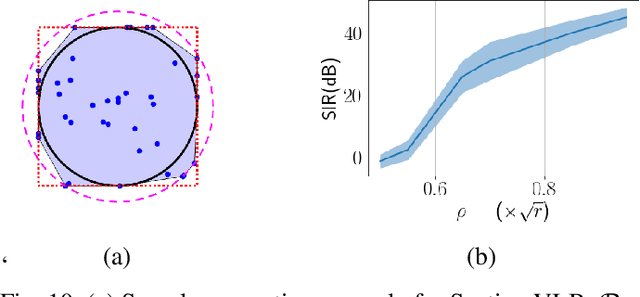
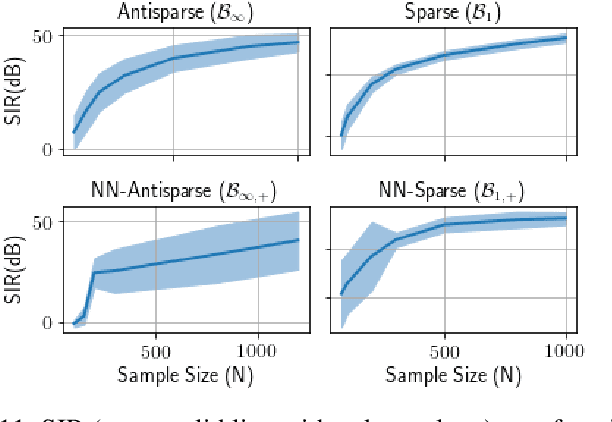
We introduce Polytopic Matrix Factorization (PMF) as a novel data decomposition approach. In this new framework, we model input data as unknown linear transformations of some latent vectors drawn from a polytope. In this sense, the article considers a semi-structured data model, in which the input matrix is modeled as the product of a full column rank matrix and a matrix containing samples from a polytope as its column vectors. The choice of polytope reflects the presumed features of the latent components and their mutual relationships. As the factorization criterion, we propose the determinant maximization (Det-Max) for the sample autocorrelation matrix of the latent vectors. We introduce a sufficient condition for identifiability, which requires that the convex hull of the latent vectors contains the maximum volume inscribed ellipsoid of the polytope with a particular tightness constraint. Based on the Det-Max criterion and the proposed identifiability condition, we show that all polytopes that satisfy a particular symmetry restriction qualify for the PMF framework. Having infinitely many polytope choices provides a form of flexibility in characterizing latent vectors. In particular, it is possible to define latent vectors with heterogeneous features, enabling the assignment of attributes such as nonnegativity and sparsity at the subvector level. The article offers examples illustrating the connection between polytope choices and the corresponding feature representations.

Blind Bounded Source Separation Using Neural Networks with Local Learning Rules

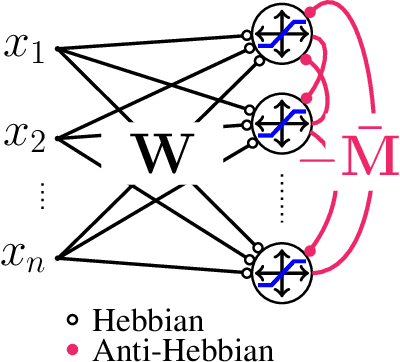
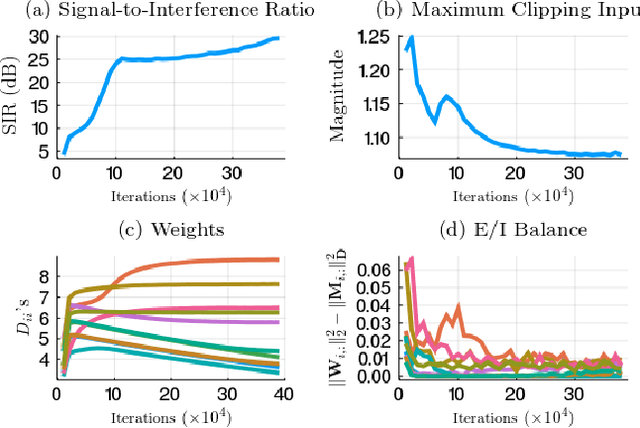
An important problem encountered by both natural and engineered signal processing systems is blind source separation. In many instances of the problem, the sources are bounded by their nature and known to be so, even though the particular bound may not be known. To separate such bounded sources from their mixtures, we propose a new optimization problem, Bounded Similarity Matching (BSM). A principled derivation of an adaptive BSM algorithm leads to a recurrent neural network with a clipping nonlinearity. The network adapts by local learning rules, satisfying an important constraint for both biological plausibility and implementability in neuromorphic hardware.

Random Input Sampling for Complex Models Using Markov Chain Monte Carlo

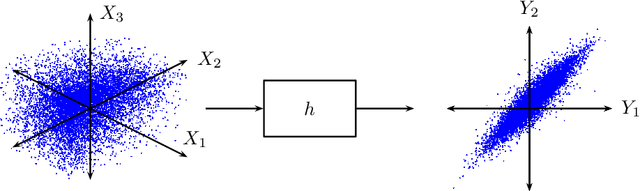
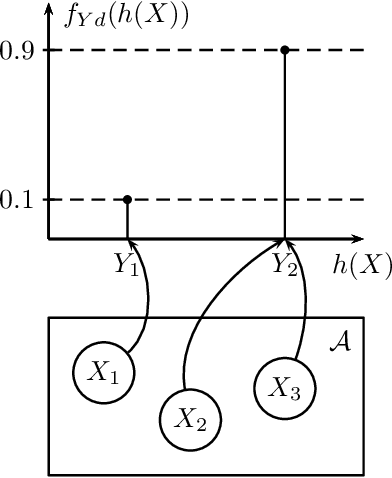
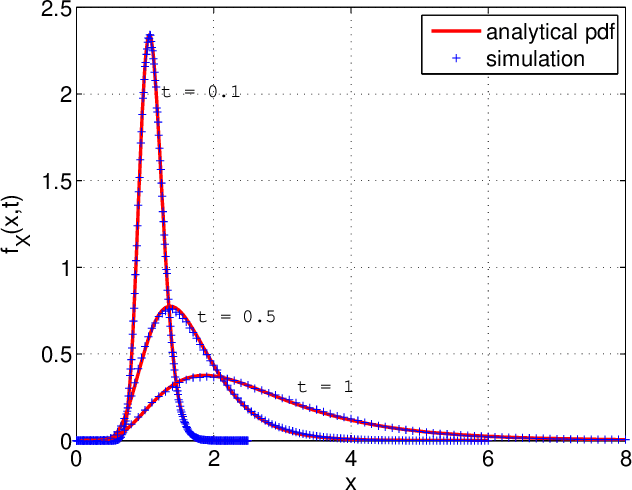
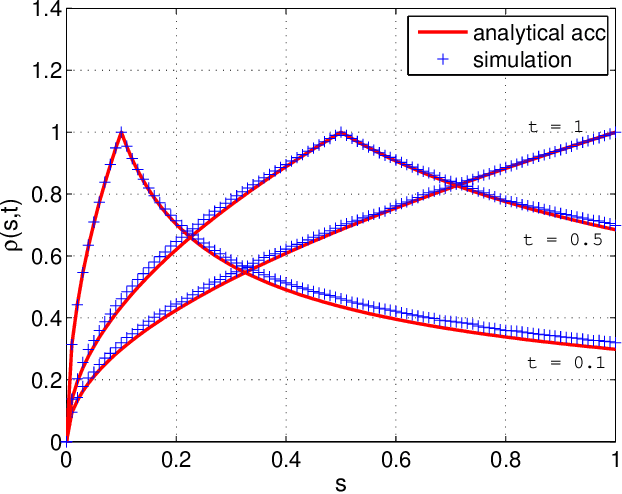
Many random processes can be simulated as the output of a deterministic model accepting random inputs. Such a model usually describes a complex mathematical or physical stochastic system and the randomness is introduced in the input variables of the model. When the statistics of the output event are known, these input variables have to be chosen in a specific way for the output to have the prescribed statistics. Because the probability distribution of the input random variables is not directly known but dictated implicitly by the statistics of the output random variables, this problem is usually intractable for classical sampling methods. Based on Markov Chain Monte Carlo we propose a novel method to sample random inputs to such models by introducing a modification to the standard Metropolis-Hastings algorithm. As an example we consider a system described by a stochastic differential equation (sde) and demonstrate how sample paths of a random process satisfying this sde can be generated with our technique.