Self-Sustaining Oscillator with Frequency Counter for Resonance Frequency Tracking in Micro- and Nanomechanical Sensing

Nanomechanical sensors based on detecting and tracking resonance frequency shifts are to be used in many applications. Various open- and closed-loop tracking schemes, all offering a trade-off between speed and precision, have been studied both theoretically and experimentally. In this work, we advocate the use of a frequency counter as a frequency shift monitor in conjunction with a self-sustaining oscillator (SSO) nanoelectromechanical system (NEMS) configuration. We derive a theoretical model for characterizing the speed and precision of frequency measurements with state-of-the-art frequency counters. Based on the understanding provided by this model, we introduce novel enhancements to frequency counters that result in a trade-off characteristics which is on a par with the other tracking schemes. We describe a low-cost field-programmable-gate array (FPGA) based implementation for the proposed frequency counter and use it with the SSO-NEMS device in order to study its frequency tracking performance. We compare the proposed approach with the phase-locked-loop based scheme both in theory and experimentally. Our results show that similar or better performance can be achieved at a substantially lower cost and improved ease-of-use. We obtain almost perfect correspondence between the theoretical model predictions and the experimental measurements.

Machine Learning and Kalman Filtering for Nanomechanical Mass Spectrometry

Nanomechanical resonant sensors are used in mass spectrometry via detection of resonance frequency jumps. There is a fundamental trade-off between detection speed and accuracy. Temporal and size resolution are limited by the resonator characteristics and noise. A Kalman filtering technique, augmented with maximum-likelihood estimation, was recently proposed as a Pareto optimal solution. We present enhancements and robust realizations for this technique, including a confidence boosted thresholding approach as well as machine learning for event detection. We describe learning techniques that are based on neural networks and boosted decision trees for temporal location and event size estimation. In the pure learning based approach that discards the Kalman filter, the raw data from the sensor are used in training a model for both location and size prediction. In the alternative approach that augments a Kalman filter, the event likelihood history is used in a binary classifier for event occurrence. Locations and sizes are predicted using maximum-likelihood, followed by a Kalman filter that continually improves the size estimate. We present detailed comparisons of the learning based schemes and the confidence boosted thresholding approach, and demonstrate robust performance for a practical realization.

Learning What to Memorize: Using Intrinsic Motivation to Form Useful Memory in Partially Observable Reinforcement Learning

Reinforcement Learning faces an important challenge in partial observable environments that has long-term dependencies. In order to learn in an ambiguous environment, an agent has to keep previous perceptions in a memory. Earlier memory based approaches use a fixed method to determine what to keep in the memory, which limits them to certain problems. In this study, we follow the idea of giving the control of the memory to the agent by allowing it to have memory-changing actions. This learning mechanism is supported by an intrinsic motivation to memorize rare observations that can help the agent to disambiguate its state in the environment. Our approach is experimented and analyzed on several partial observable tasks with long-term dependencies and compared with other memory based methods.

Random Input Sampling for Complex Models Using Markov Chain Monte Carlo

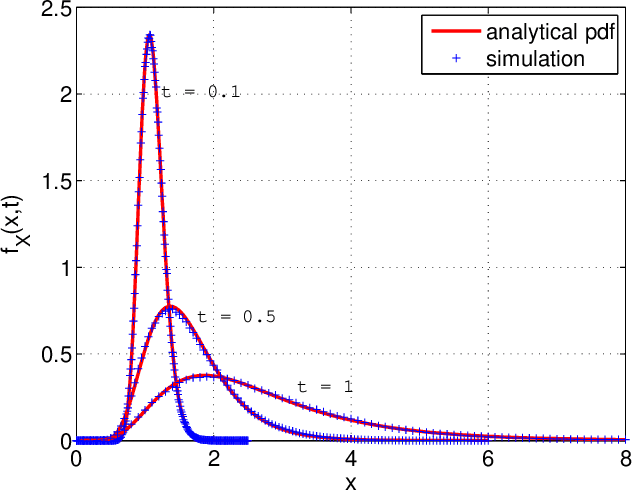
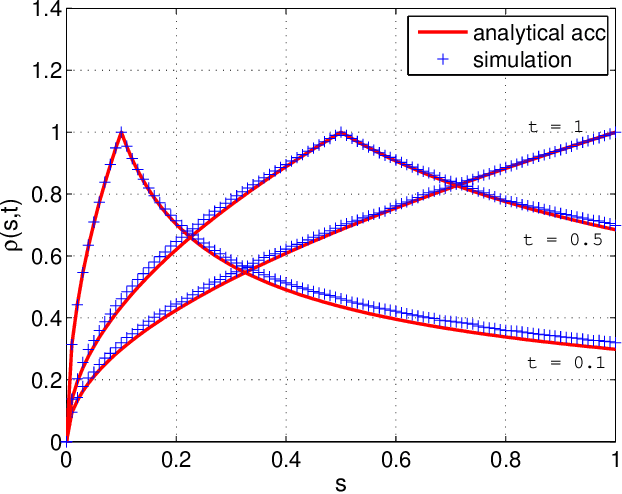
Many random processes can be simulated as the output of a deterministic model accepting random inputs. Such a model usually describes a complex mathematical or physical stochastic system and the randomness is introduced in the input variables of the model. When the statistics of the output event are known, these input variables have to be chosen in a specific way for the output to have the prescribed statistics. Because the probability distribution of the input random variables is not directly known but dictated implicitly by the statistics of the output random variables, this problem is usually intractable for classical sampling methods. Based on Markov Chain Monte Carlo we propose a novel method to sample random inputs to such models by introducing a modification to the standard Metropolis-Hastings algorithm. As an example we consider a system described by a stochastic differential equation (sde) and demonstrate how sample paths of a random process satisfying this sde can be generated with our technique.