Random Input Sampling for Complex Models Using Markov Chain Monte Carlo
Paper and Code
Nov 20, 2012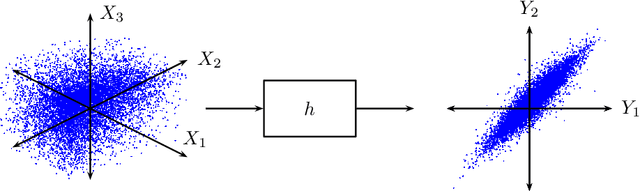
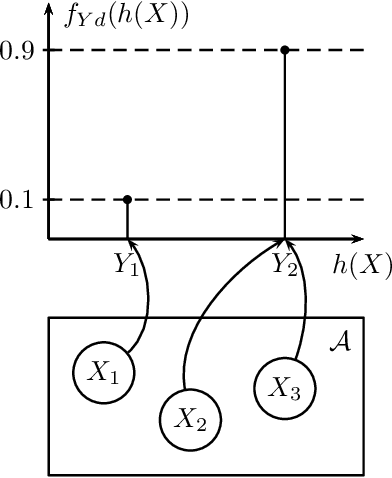
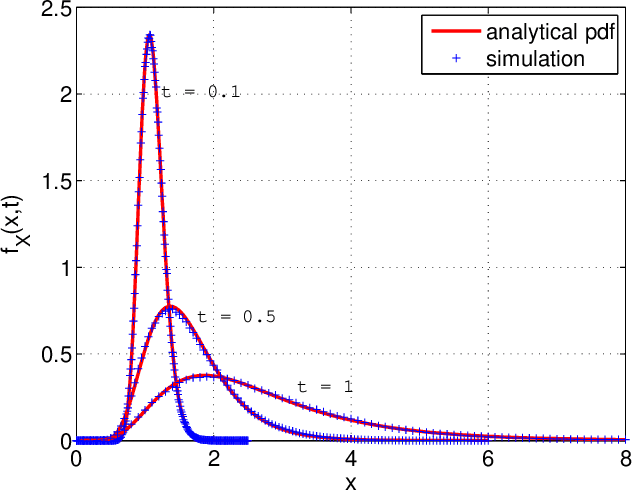
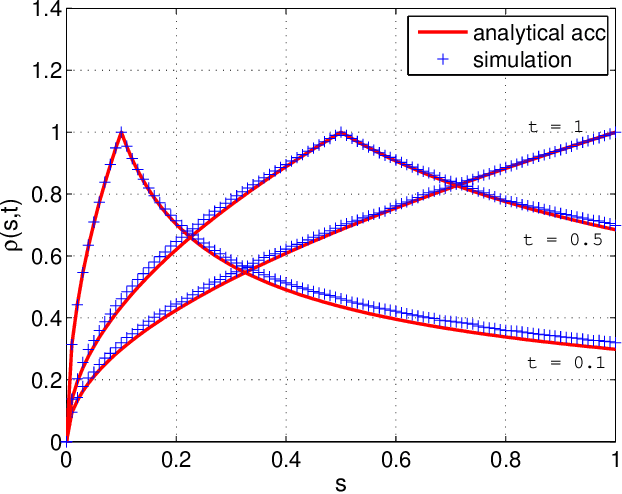
Many random processes can be simulated as the output of a deterministic model accepting random inputs. Such a model usually describes a complex mathematical or physical stochastic system and the randomness is introduced in the input variables of the model. When the statistics of the output event are known, these input variables have to be chosen in a specific way for the output to have the prescribed statistics. Because the probability distribution of the input random variables is not directly known but dictated implicitly by the statistics of the output random variables, this problem is usually intractable for classical sampling methods. Based on Markov Chain Monte Carlo we propose a novel method to sample random inputs to such models by introducing a modification to the standard Metropolis-Hastings algorithm. As an example we consider a system described by a stochastic differential equation (sde) and demonstrate how sample paths of a random process satisfying this sde can be generated with our technique.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge