A Bayesian Perspective for Determinant Minimization Based Robust Structured Matrix Factorizatio

We introduce a Bayesian perspective for the structured matrix factorization problem. The proposed framework provides a probabilistic interpretation for existing geometric methods based on determinant minimization. We model input data vectors as linear transformations of latent vectors drawn from a distribution uniform over a particular domain reflecting structural assumptions, such as the probability simplex in Nonnegative Matrix Factorization and polytopes in Polytopic Matrix Factorization. We represent the rows of the linear transformation matrix as vectors generated independently from a normal distribution whose covariance matrix is inverse Wishart distributed. We show that the corresponding maximum a posteriori estimation problem boils down to the robust determinant minimization approach for structured matrix factorization, providing insights about parameter selections and potential algorithmic extensions.

Polytopic Matrix Factorization: Determinant Maximization Based Criterion and Identifiability

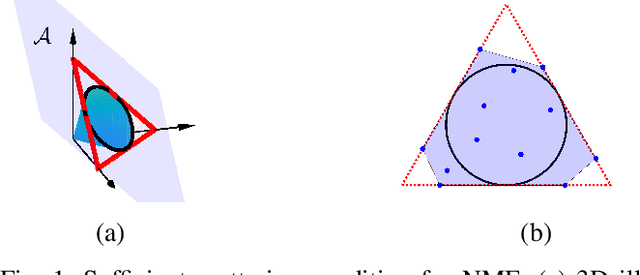
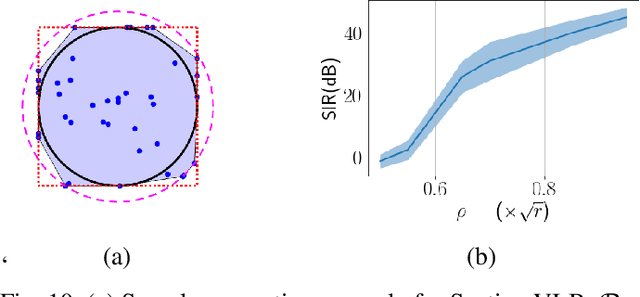
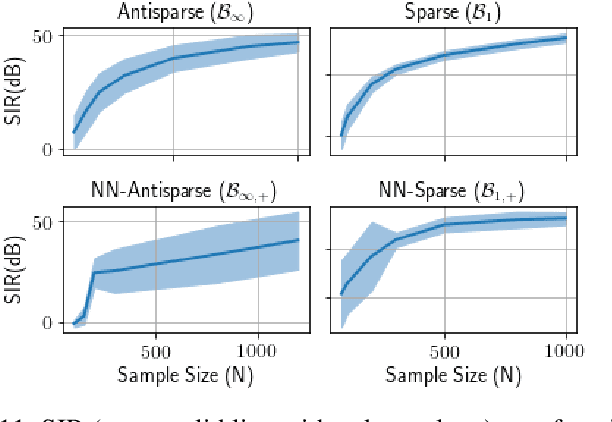
We introduce Polytopic Matrix Factorization (PMF) as a novel data decomposition approach. In this new framework, we model input data as unknown linear transformations of some latent vectors drawn from a polytope. In this sense, the article considers a semi-structured data model, in which the input matrix is modeled as the product of a full column rank matrix and a matrix containing samples from a polytope as its column vectors. The choice of polytope reflects the presumed features of the latent components and their mutual relationships. As the factorization criterion, we propose the determinant maximization (Det-Max) for the sample autocorrelation matrix of the latent vectors. We introduce a sufficient condition for identifiability, which requires that the convex hull of the latent vectors contains the maximum volume inscribed ellipsoid of the polytope with a particular tightness constraint. Based on the Det-Max criterion and the proposed identifiability condition, we show that all polytopes that satisfy a particular symmetry restriction qualify for the PMF framework. Having infinitely many polytope choices provides a form of flexibility in characterizing latent vectors. In particular, it is possible to define latent vectors with heterogeneous features, enabling the assignment of attributes such as nonnegativity and sparsity at the subvector level. The article offers examples illustrating the connection between polytope choices and the corresponding feature representations.