Biologically-Plausible Determinant Maximization Neural Networks for Blind Separation of Correlated Sources
Paper and Code
Sep 27, 2022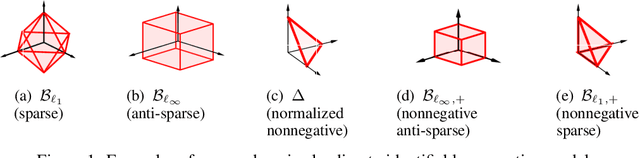

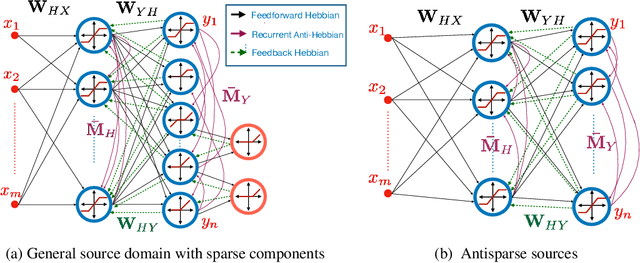
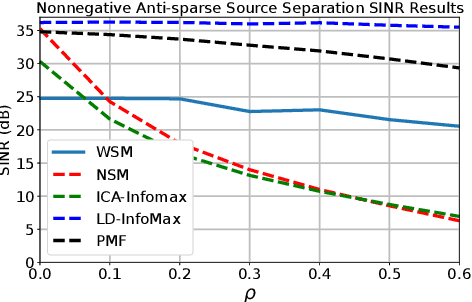
Extraction of latent sources of complex stimuli is critical for making sense of the world. While the brain solves this blind source separation (BSS) problem continuously, its algorithms remain unknown. Previous work on biologically-plausible BSS algorithms assumed that observed signals are linear mixtures of statistically independent or uncorrelated sources, limiting the domain of applicability of these algorithms. To overcome this limitation, we propose novel biologically-plausible neural networks for the blind separation of potentially dependent/correlated sources. Differing from previous work, we assume some general geometric, not statistical, conditions on the source vectors allowing separation of potentially dependent/correlated sources. Concretely, we assume that the source vectors are sufficiently scattered in their domains which can be described by certain polytopes. Then, we consider recovery of these sources by the Det-Max criterion, which maximizes the determinant of the output correlation matrix to enforce a similar spread for the source estimates. Starting from this normative principle, and using a weighted similarity matching approach that enables arbitrary linear transformations adaptable by local learning rules, we derive two-layer biologically-plausible neural network algorithms that can separate mixtures into sources coming from a variety of source domains. We demonstrate that our algorithms outperform other biologically-plausible BSS algorithms on correlated source separation problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge