Bariscan Bozkurt
Density Ratio-Free Doubly Robust Proxy Causal Learning
May 26, 2025Abstract:We study the problem of causal function estimation in the Proxy Causal Learning (PCL) framework, where confounders are not observed but proxies for the confounders are available. Two main approaches have been proposed: outcome bridge-based and treatment bridge-based methods. In this work, we propose two kernel-based doubly robust estimators that combine the strengths of both approaches, and naturally handle continuous and high-dimensional variables. Our identification strategy builds on a recent density ratio-free method for treatment bridge-based PCL; furthermore, in contrast to previous approaches, it does not require indicator functions or kernel smoothing over the treatment variable. These properties make it especially well-suited for continuous or high-dimensional treatments. By using kernel mean embeddings, we have closed-form solutions and strong consistency guarantees. Our estimators outperform existing methods on PCL benchmarks, including a prior doubly robust method that requires both kernel smoothing and density ratio estimation.
Density Ratio-based Proxy Causal Learning Without Density Ratios
Mar 11, 2025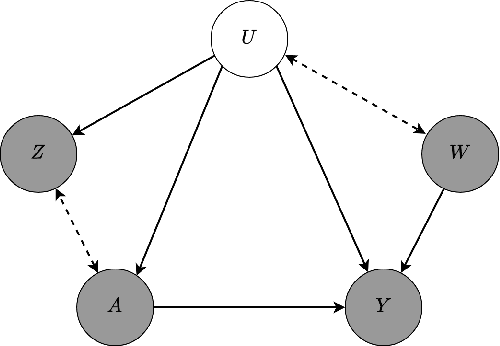
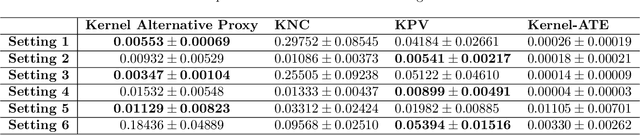
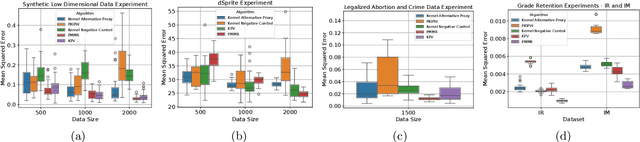
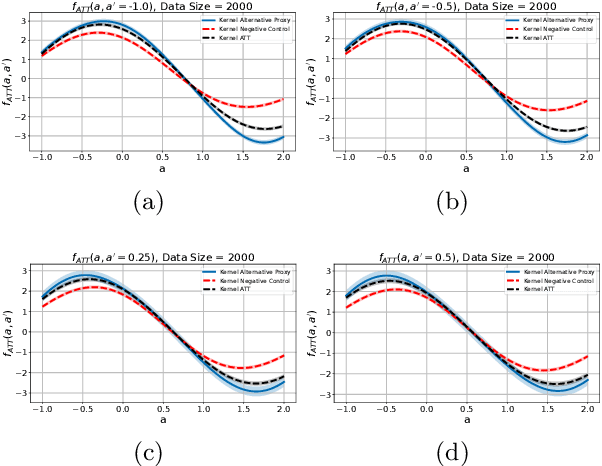
Abstract:We address the setting of Proxy Causal Learning (PCL), which has the goal of estimating causal effects from observed data in the presence of hidden confounding. Proxy methods accomplish this task using two proxy variables related to the latent confounder: a treatment proxy (related to the treatment) and an outcome proxy (related to the outcome). Two approaches have been proposed to perform causal effect estimation given proxy variables; however only one of these has found mainstream acceptance, since the other was understood to require density ratio estimation - a challenging task in high dimensions. In the present work, we propose a practical and effective implementation of the second approach, which bypasses explicit density ratio estimation and is suitable for continuous and high-dimensional treatments. We employ kernel ridge regression to derive estimators, resulting in simple closed-form solutions for dose-response and conditional dose-response curves, along with consistency guarantees. Our methods empirically demonstrate superior or comparable performance to existing frameworks on synthetic and real-world datasets.
Correlative Information Maximization: A Biologically Plausible Approach to Supervised Deep Neural Networks without Weight Symmetry
Jun 09, 2023Abstract:The backpropagation algorithm has experienced remarkable success in training large-scale artificial neural networks, however, its biological-plausibility is disputed, and it remains an open question whether the brain employs supervised learning mechanisms akin to it. Here, we propose correlative information maximization between layer activations as an alternative normative approach to describe the signal propagation in biological neural networks in both forward and backward directions. This new framework addresses many concerns about the biological-plausibility of conventional artificial neural networks and the backpropagation algorithm. The coordinate descent-based optimization of the corresponding objective, combined with the mean square error loss function for fitting labeled supervision data, gives rise to a neural network structure that emulates a more biologically realistic network of multi-compartment pyramidal neurons with dendritic processing and lateral inhibitory neurons. Furthermore, our approach provides a natural resolution to the weight symmetry problem between forward and backward signal propagation paths, a significant critique against the plausibility of the conventional backpropagation algorithm. This is achieved by leveraging two alternative, yet equivalent forms of the correlative mutual information objective. These alternatives intrinsically lead to forward and backward prediction networks without weight symmetry issues, providing a compelling solution to this long-standing challenge.
Correlative Information Maximization Based Biologically Plausible Neural Networks for Correlated Source Separation
Oct 09, 2022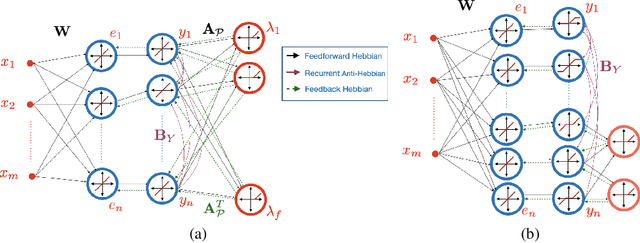

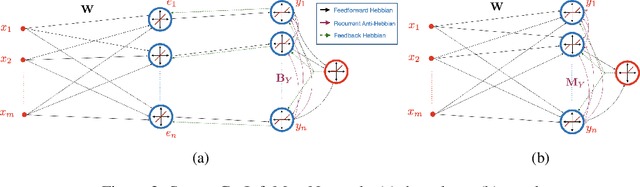

Abstract:The brain effortlessly extracts latent causes of stimuli, but how it does this at the network level remains unknown. Most prior attempts at this problem proposed neural networks that implement independent component analysis which works under the limitation that latent causes are mutually independent. Here, we relax this limitation and propose a biologically plausible neural network that extracts correlated latent sources by exploiting information about their domains. To derive this network, we choose maximum correlative information transfer from inputs to outputs as the separation objective under the constraint that the outputs are restricted to their presumed sets. The online formulation of this optimization problem naturally leads to neural networks with local learning rules. Our framework incorporates infinitely many source domain choices and flexibly models complex latent structures. Choices of simplex or polytopic source domains result in networks with piecewise-linear activation functions. We provide numerical examples to demonstrate the superior correlated source separation capability for both synthetic and natural sources.
Biologically-Plausible Determinant Maximization Neural Networks for Blind Separation of Correlated Sources
Sep 27, 2022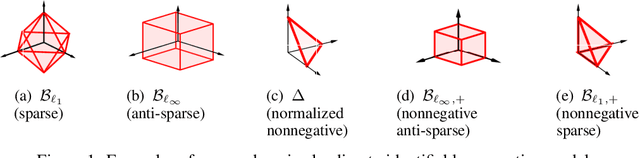

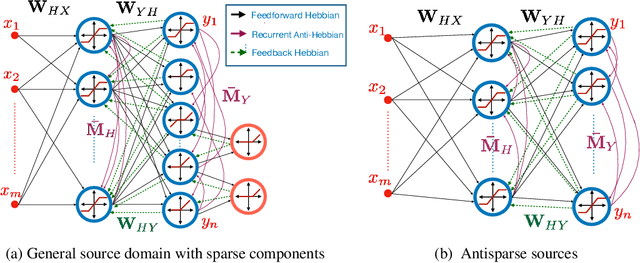
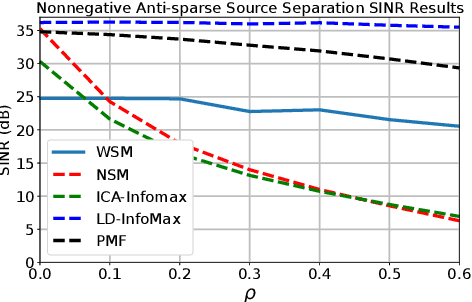
Abstract:Extraction of latent sources of complex stimuli is critical for making sense of the world. While the brain solves this blind source separation (BSS) problem continuously, its algorithms remain unknown. Previous work on biologically-plausible BSS algorithms assumed that observed signals are linear mixtures of statistically independent or uncorrelated sources, limiting the domain of applicability of these algorithms. To overcome this limitation, we propose novel biologically-plausible neural networks for the blind separation of potentially dependent/correlated sources. Differing from previous work, we assume some general geometric, not statistical, conditions on the source vectors allowing separation of potentially dependent/correlated sources. Concretely, we assume that the source vectors are sufficiently scattered in their domains which can be described by certain polytopes. Then, we consider recovery of these sources by the Det-Max criterion, which maximizes the determinant of the output correlation matrix to enforce a similar spread for the source estimates. Starting from this normative principle, and using a weighted similarity matching approach that enables arbitrary linear transformations adaptable by local learning rules, we derive two-layer biologically-plausible neural network algorithms that can separate mixtures into sources coming from a variety of source domains. We demonstrate that our algorithms outperform other biologically-plausible BSS algorithms on correlated source separation problems.
On Identifiable Polytope Characterization for Polytopic Matrix Factorization
Apr 25, 2022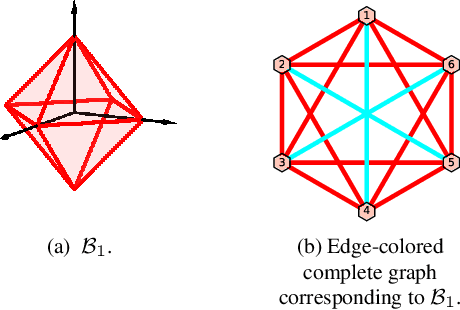
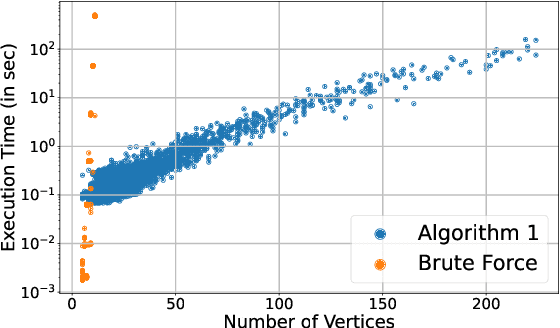
Abstract:Polytopic matrix factorization (PMF) is a recently introduced matrix decomposition method in which the data vectors are modeled as linear transformations of samples from a polytope. The successful recovery of the original factors in the generative PMF model is conditioned on the "identifiability" of the chosen polytope. In this article, we investigate the problem of determining the identifiability of a polytope. The identifiability condition requires the polytope to be permutation-and/or-sign-only invariant. We show how this problem can be efficiently solved by using a graph automorphism algorithm. In particular, we show that checking only the generating set of the linear automorphism group of a polytope, which corresponds to the automorphism group of an edge-colored complete graph, is sufficient. This property prevents checking all the elements of the permutation group, which requires factorial algorithm complexity. We demonstrate the feasibility of the proposed approach through some numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge