On Identifiable Polytope Characterization for Polytopic Matrix Factorization
Paper and Code
Apr 25, 2022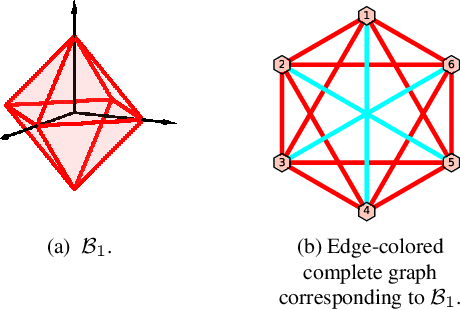
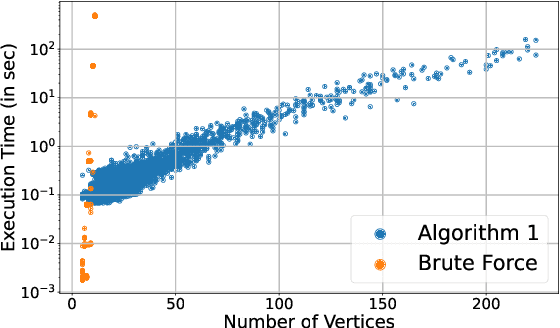
Polytopic matrix factorization (PMF) is a recently introduced matrix decomposition method in which the data vectors are modeled as linear transformations of samples from a polytope. The successful recovery of the original factors in the generative PMF model is conditioned on the "identifiability" of the chosen polytope. In this article, we investigate the problem of determining the identifiability of a polytope. The identifiability condition requires the polytope to be permutation-and/or-sign-only invariant. We show how this problem can be efficiently solved by using a graph automorphism algorithm. In particular, we show that checking only the generating set of the linear automorphism group of a polytope, which corresponds to the automorphism group of an edge-colored complete graph, is sufficient. This property prevents checking all the elements of the permutation group, which requires factorial algorithm complexity. We demonstrate the feasibility of the proposed approach through some numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge