An Information Maximization Based Blind Source Separation Approach for Dependent and Independent Sources
Paper and Code
May 02, 2022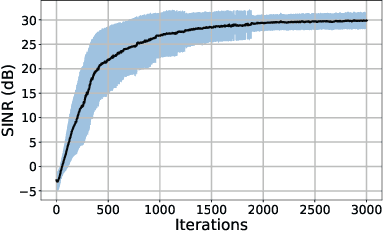
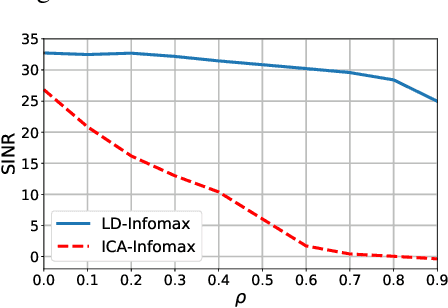
We introduce a new information maximization (infomax) approach for the blind source separation problem. The proposed framework provides an information-theoretic perspective for determinant maximization-based structured matrix factorization methods such as nonnegative and polytopic matrix factorization. For this purpose, we use an alternative joint entropy measure based on the log-determinant of covariance, which we refer to as log-determinant (LD) entropy. The corresponding (LD) mutual information between two vectors reflects a level of their correlation. We pose the infomax BSS criterion as the maximization of the LD-mutual information between the input and output of the separator under the constraint that the output vectors lie in a presumed domain set. In contrast to the ICA infomax approach, the proposed information maximization approach can separate both dependent and independent sources. Furthermore, we can provide a finite sample guarantee for the perfect separation condition in the noiseless case.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge