Risk and cross validation in ridge regression with correlated samples

Recent years have seen substantial advances in our understanding of high-dimensional ridge regression, but existing theories assume that training examples are independent. By leveraging recent techniques from random matrix theory and free probability, we provide sharp asymptotics for the in- and out-of-sample risks of ridge regression when the data points have arbitrary correlations. We demonstrate that in this setting, the generalized cross validation estimator (GCV) fails to correctly predict the out-of-sample risk. However, in the case where the noise residuals have the same correlations as the data points, one can modify the GCV to yield an efficiently-computable unbiased estimator that concentrates in the high-dimensional limit, which we dub CorrGCV. We further extend our asymptotic analysis to the case where the test point has nontrivial correlations with the training set, a setting often encountered in time series forecasting. Assuming knowledge of the correlation structure of the time series, this again yields an extension of the GCV estimator, and sharply characterizes the degree to which such test points yield an overly optimistic prediction of long-time risk. We validate the predictions of our theory across a variety of high dimensional data.

Nadaraya-Watson kernel smoothing as a random energy model

We investigate the behavior of the Nadaraya-Watson kernel smoothing estimator in high dimensions using its relationship to the random energy model and to dense associative memories.

Spectral regularization for adversarially-robust representation learning

The vulnerability of neural network classifiers to adversarial attacks is a major obstacle to their deployment in safety-critical applications. Regularization of network parameters during training can be used to improve adversarial robustness and generalization performance. Usually, the network is regularized end-to-end, with parameters at all layers affected by regularization. However, in settings where learning representations is key, such as self-supervised learning (SSL), layers after the feature representation will be discarded when performing inference. For these models, regularizing up to the feature space is more suitable. To this end, we propose a new spectral regularizer for representation learning that encourages black-box adversarial robustness in downstream classification tasks. In supervised classification settings, we show empirically that this method is more effective in boosting test accuracy and robustness than previously-proposed methods that regularize all layers of the network. We then show that this method improves the adversarial robustness of classifiers using representations learned with self-supervised training or transferred from another classification task. In all, our work begins to unveil how representational structure affects adversarial robustness.

Asymptotic theory of in-context learning by linear attention

Transformers have a remarkable ability to learn and execute tasks based on examples provided within the input itself, without explicit prior training. It has been argued that this capability, known as in-context learning (ICL), is a cornerstone of Transformers' success, yet questions about the necessary sample complexity, pretraining task diversity, and context length for successful ICL remain unresolved. Here, we provide a precise answer to these questions in an exactly solvable model of ICL of a linear regression task by linear attention. We derive sharp asymptotics for the learning curve in a phenomenologically-rich scaling regime where the token dimension is taken to infinity; the context length and pretraining task diversity scale proportionally with the token dimension; and the number of pretraining examples scales quadratically. We demonstrate a double-descent learning curve with increasing pretraining examples, and uncover a phase transition in the model's behavior between low and high task diversity regimes: In the low diversity regime, the model tends toward memorization of training tasks, whereas in the high diversity regime, it achieves genuine in-context learning and generalization beyond the scope of pretrained tasks. These theoretical insights are empirically validated through experiments with both linear attention and full nonlinear Transformer architectures.

Scaling and renormalization in high-dimensional regression

This paper presents a succinct derivation of the training and generalization performance of a variety of high-dimensional ridge regression models using the basic tools of random matrix theory and free probability. We provide an introduction and review of recent results on these topics, aimed at readers with backgrounds in physics and deep learning. Analytic formulas for the training and generalization errors are obtained in a few lines of algebra directly from the properties of the $S$-transform of free probability. This allows for a straightforward identification of the sources of power-law scaling in model performance. We compute the generalization error of a broad class of random feature models. We find that in all models, the $S$-transform corresponds to the train-test generalization gap, and yields an analogue of the generalized-cross-validation estimator. Using these techniques, we derive fine-grained bias-variance decompositions for a very general class of random feature models with structured covariates. These novel results allow us to discover a scaling regime for random feature models where the variance due to the features limits performance in the overparameterized setting. We also demonstrate how anisotropic weight structure in random feature models can limit performance and lead to nontrivial exponents for finite-width corrections in the overparameterized setting. Our results extend and provide a unifying perspective on earlier models of neural scaling laws.

Long Sequence Hopfield Memory

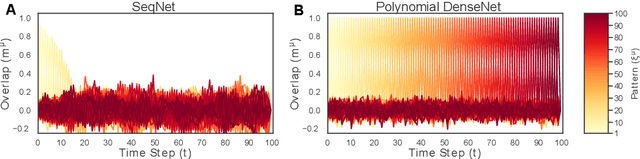
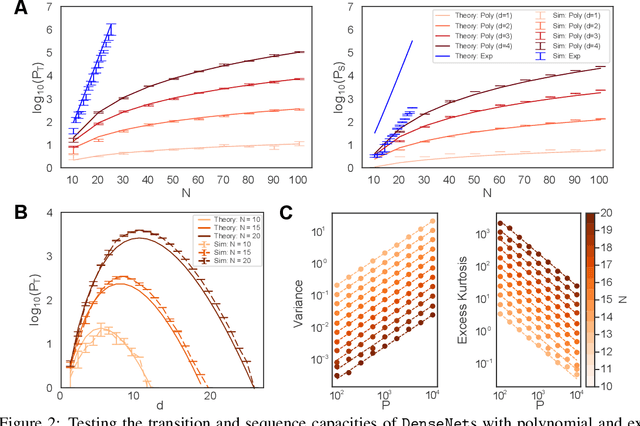
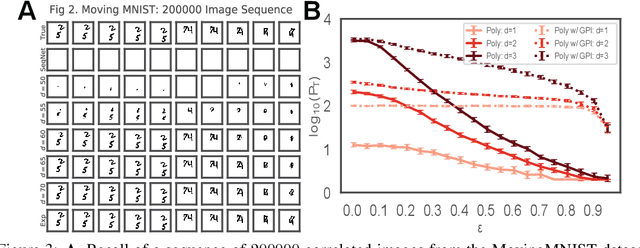
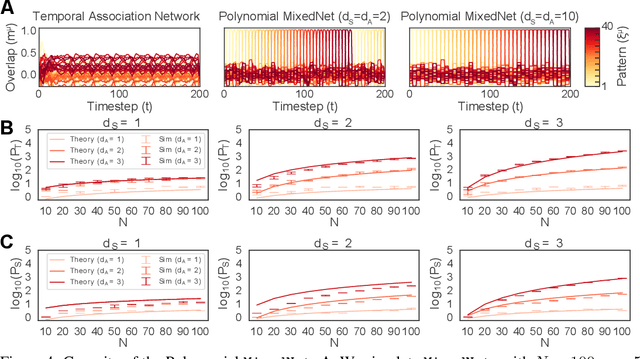
Sequence memory is an essential attribute of natural and artificial intelligence that enables agents to encode, store, and retrieve complex sequences of stimuli and actions. Computational models of sequence memory have been proposed where recurrent Hopfield-like neural networks are trained with temporally asymmetric Hebbian rules. However, these networks suffer from limited sequence capacity (maximal length of the stored sequence) due to interference between the memories. Inspired by recent work on Dense Associative Memories, we expand the sequence capacity of these models by introducing a nonlinear interaction term, enhancing separation between the patterns. We derive novel scaling laws for sequence capacity with respect to network size, significantly outperforming existing scaling laws for models based on traditional Hopfield networks, and verify these theoretical results with numerical simulation. Moreover, we introduce a generalized pseudoinverse rule to recall sequences of highly correlated patterns. Finally, we extend this model to store sequences with variable timing between states' transitions and describe a biologically-plausible implementation, with connections to motor neuroscience.

Learning curves for deep structured Gaussian feature models

In recent years, significant attention in deep learning theory has been devoted to analyzing the generalization performance of models with multiple layers of Gaussian random features. However, few works have considered the effect of feature anisotropy; most assume that features are generated using independent and identically distributed Gaussian weights. Here, we derive learning curves for models with many layers of structured Gaussian features. We show that allowing correlations between the rows of the first layer of features can aid generalization, while structure in later layers is generally detrimental. Our results shed light on how weight structure affects generalization in a simple class of solvable models.

Neural networks learn to magnify areas near decision boundaries

We study how training molds the Riemannian geometry induced by neural network feature maps. At infinite width, neural networks with random parameters induce highly symmetric metrics on input space. Feature learning in networks trained to perform classification tasks magnifies local areas along decision boundaries. These changes are consistent with previously proposed geometric approaches for hand-tuning of kernel methods to improve generalization.

Contrasting random and learned features in deep Bayesian linear regression

Understanding how feature learning affects generalization is among the foremost goals of modern deep learning theory. Here, we study how the ability to learn representations affects the generalization performance of a simple class of models: deep Bayesian linear neural networks trained on unstructured Gaussian data. By comparing deep random feature models to deep networks in which all layers are trained, we provide a detailed characterization of the interplay between width, depth, data density, and prior mismatch. We show that both models display sample-wise double-descent behavior in the presence of label noise. Random feature models can also display model-wise double-descent if there are narrow bottleneck layers, while deep networks do not show these divergences. Random feature models can have particular widths that are optimal for generalization at a given data density, while making neural networks as wide or as narrow as possible is always optimal. Moreover, we show that the leading-order correction to the kernel-limit learning curve cannot distinguish between random feature models and deep networks in which all layers are trained. Taken together, our findings begin to elucidate how architectural details affect generalization performance in this simple class of deep regression models.

On neural network kernels and the storage capacity problem

In this short note, we reify the connection between work on the storage capacity problem in wide two-layer treelike neural networks and the rapidly-growing body of literature on kernel limits of wide neural networks. Concretely, we observe that the "effective order parameter" studied in the statistical mechanics literature is exactly equivalent to the infinite-width Neural Network Gaussian Process Kernel. This correspondence connects the expressivity and trainability of wide two-layer neural networks.