POCO: Scalable Neural Forecasting through Population Conditioning

Predicting future neural activity is a core challenge in modeling brain dynamics, with applications ranging from scientific investigation to closed-loop neurotechnology. While recent models of population activity emphasize interpretability and behavioral decoding, neural forecasting-particularly across multi-session, spontaneous recordings-remains underexplored. We introduce POCO, a unified forecasting model that combines a lightweight univariate forecaster with a population-level encoder to capture both neuron-specific and brain-wide dynamics. Trained across five calcium imaging datasets spanning zebrafish, mice, and C. elegans, POCO achieves state-of-the-art accuracy at cellular resolution in spontaneous behaviors. After pre-training, POCO rapidly adapts to new recordings with minimal fine-tuning. Notably, POCO's learned unit embeddings recover biologically meaningful structure-such as brain region clustering-without any anatomical labels. Our comprehensive analysis reveals several key factors influencing performance, including context length, session diversity, and preprocessing. Together, these results position POCO as a scalable and adaptable approach for cross-session neural forecasting and offer actionable insights for future model design. By enabling accurate, generalizable forecasting models of neural dynamics across individuals and species, POCO lays the groundwork for adaptive neurotechnologies and large-scale efforts for neural foundation models.

No Free Lunch From Random Feature Ensembles

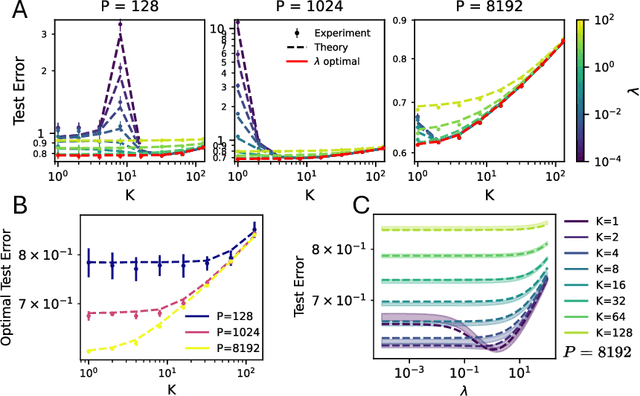
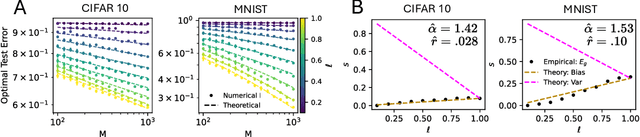
Given a budget on total model size, one must decide whether to train a single, large neural network or to combine the predictions of many smaller networks. We study this trade-off for ensembles of random-feature ridge regression models. We prove that when a fixed number of trainable parameters are partitioned among $K$ independently trained models, $K=1$ achieves optimal performance, provided the ridge parameter is optimally tuned. We then derive scaling laws which describe how the test risk of an ensemble of regression models decays with its total size. We identify conditions on the kernel and task eigenstructure under which ensembles can achieve near-optimal scaling laws. Training ensembles of deep convolutional neural networks on CIFAR-10 and a transformer architecture on C4, we find that a single large network outperforms any ensemble of networks with the same total number of parameters, provided the weight decay and feature-learning strength are tuned to their optimal values.

Infinite Limits of Multi-head Transformer Dynamics

In this work, we analyze various scaling limits of the training dynamics of transformer models in the feature learning regime. We identify the set of parameterizations that admit well-defined infinite width and depth limits, allowing the attention layers to update throughout training--a relevant notion of feature learning in these models. We then use tools from dynamical mean field theory (DMFT) to analyze various infinite limits (infinite key/query dimension, infinite heads, and infinite depth) which have different statistical descriptions depending on which infinite limit is taken and how attention layers are scaled. We provide numerical evidence of convergence to the limits and discuss how the parameterization qualitatively influences learned features.

Long Sequence Hopfield Memory

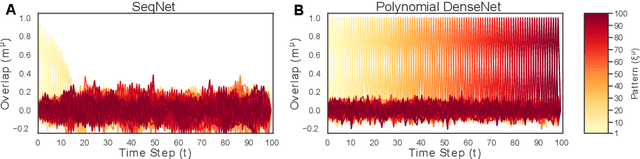
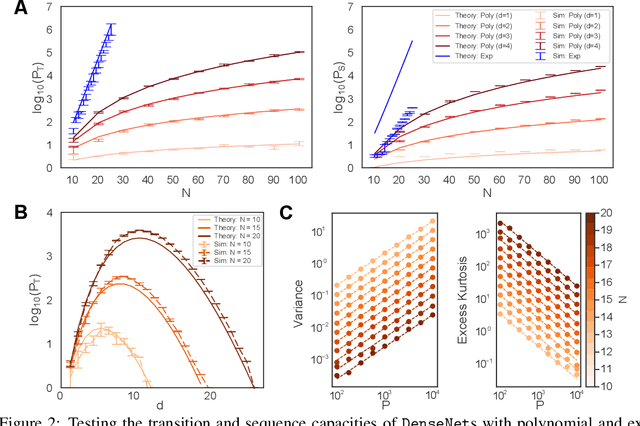
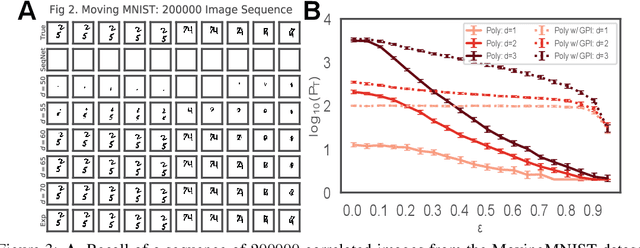
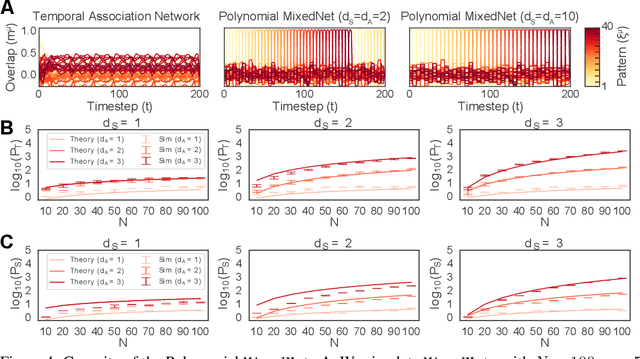
Sequence memory is an essential attribute of natural and artificial intelligence that enables agents to encode, store, and retrieve complex sequences of stimuli and actions. Computational models of sequence memory have been proposed where recurrent Hopfield-like neural networks are trained with temporally asymmetric Hebbian rules. However, these networks suffer from limited sequence capacity (maximal length of the stored sequence) due to interference between the memories. Inspired by recent work on Dense Associative Memories, we expand the sequence capacity of these models by introducing a nonlinear interaction term, enhancing separation between the patterns. We derive novel scaling laws for sequence capacity with respect to network size, significantly outperforming existing scaling laws for models based on traditional Hopfield networks, and verify these theoretical results with numerical simulation. Moreover, we introduce a generalized pseudoinverse rule to recall sequences of highly correlated patterns. Finally, we extend this model to store sequences with variable timing between states' transitions and describe a biologically-plausible implementation, with connections to motor neuroscience.