Exploring the Energy Landscape of RBMs: Reciprocal Space Insights into Bosons, Hierarchical Learning and Symmetry Breaking

Deep generative models have become ubiquitous due to their ability to learn and sample from complex distributions. Despite the proliferation of various frameworks, the relationships among these models remain largely unexplored, a gap that hinders the development of a unified theory of AI learning. We address two central challenges: clarifying the connections between different deep generative models and deepening our understanding of their learning mechanisms. We focus on Restricted Boltzmann Machines (RBMs), known for their universal approximation capabilities for discrete distributions. By introducing a reciprocal space formulation, we reveal a connection between RBMs, diffusion processes, and coupled Bosons. We show that at initialization, the RBM operates at a saddle point, where the local curvature is determined by the singular values, whose distribution follows the Marcenko-Pastur law and exhibits rotational symmetry. During training, this rotational symmetry is broken due to hierarchical learning, where different degrees of freedom progressively capture features at multiple levels of abstraction. This leads to a symmetry breaking in the energy landscape, reminiscent of Landau theory. This symmetry breaking in the energy landscape is characterized by the singular values and the weight matrix eigenvector matrix. We derive the corresponding free energy in a mean-field approximation. We show that in the limit of infinite size RBM, the reciprocal variables are Gaussian distributed. Our findings indicate that in this regime, there will be some modes for which the diffusion process will not converge to the Boltzmann distribution. To illustrate our results, we trained replicas of RBMs with different hidden layer sizes using the MNIST dataset. Our findings bridge the gap between disparate generative frameworks and also shed light on the processes underpinning learning in generative models.

Bayesian RG Flow in Neural Network Field Theories

The Neural Network Field Theory correspondence (NNFT) is a mapping from neural network (NN) architectures into the space of statistical field theories (SFTs). The Bayesian renormalization group (BRG) is an information-theoretic coarse graining scheme that generalizes the principles of the Exact Renormalization Group (ERG) to arbitrarily parameterized probability distributions, including those of NNs. In BRG, coarse graining is performed in parameter space with respect to an information-theoretic distinguishability scale set by the Fisher information metric. In this paper, we unify NNFT and BRG to form a powerful new framework for exploring the space of NNs and SFTs, which we coin BRG-NNFT. With BRG-NNFT, NN training dynamics can be interpreted as inducing a flow in the space of SFTs from the information-theoretic `IR' $\rightarrow$ `UV'. Conversely, applying an information-shell coarse graining to the trained network's parameters induces a flow in the space of SFTs from the information-theoretic `UV' $\rightarrow$ `IR'. When the information-theoretic cutoff scale coincides with a standard momentum scale, BRG is equivalent to ERG. We demonstrate the BRG-NNFT correspondence on two analytically tractable examples. First, we construct BRG flows for trained, infinite-width NNs, of arbitrary depth, with generic activation functions. As a special case, we then restrict to architectures with a single infinitely-wide layer, scalar outputs, and generalized cos-net activations. In this case, we show that BRG coarse-graining corresponds exactly to the momentum-shell ERG flow of a free scalar SFT. Our analytic results are corroborated by a numerical experiment in which an ensemble of asymptotically wide NNs are trained and subsequently renormalized using an information-shell BRG scheme.

Asymptotic theory of in-context learning by linear attention

Transformers have a remarkable ability to learn and execute tasks based on examples provided within the input itself, without explicit prior training. It has been argued that this capability, known as in-context learning (ICL), is a cornerstone of Transformers' success, yet questions about the necessary sample complexity, pretraining task diversity, and context length for successful ICL remain unresolved. Here, we provide a precise answer to these questions in an exactly solvable model of ICL of a linear regression task by linear attention. We derive sharp asymptotics for the learning curve in a phenomenologically-rich scaling regime where the token dimension is taken to infinity; the context length and pretraining task diversity scale proportionally with the token dimension; and the number of pretraining examples scales quadratically. We demonstrate a double-descent learning curve with increasing pretraining examples, and uncover a phase transition in the model's behavior between low and high task diversity regimes: In the low diversity regime, the model tends toward memorization of training tasks, whereas in the high diversity regime, it achieves genuine in-context learning and generalization beyond the scope of pretrained tasks. These theoretical insights are empirically validated through experiments with both linear attention and full nonlinear Transformer architectures.

Wilsonian Renormalization of Neural Network Gaussian Processes

Separating relevant and irrelevant information is key to any modeling process or scientific inquiry. Theoretical physics offers a powerful tool for achieving this in the form of the renormalization group (RG). Here we demonstrate a practical approach to performing Wilsonian RG in the context of Gaussian Process (GP) Regression. We systematically integrate out the unlearnable modes of the GP kernel, thereby obtaining an RG flow of the Gaussian Process in which the data plays the role of the energy scale. In simple cases, this results in a universal flow of the ridge parameter, which becomes input-dependent in the richer scenario in which non-Gaussianities are included. In addition to being analytically tractable, this approach goes beyond structural analogies between RG and neural networks by providing a natural connection between RG flow and learnable vs. unlearnable modes. Studying such flows may improve our understanding of feature learning in deep neural networks, and identify potential universality classes in these models.

Neural Network Field Theories: Non-Gaussianity, Actions, and Locality

Both the path integral measure in field theory and ensembles of neural networks describe distributions over functions. When the central limit theorem can be applied in the infinite-width (infinite-$N$) limit, the ensemble of networks corresponds to a free field theory. Although an expansion in $1/N$ corresponds to interactions in the field theory, others, such as in a small breaking of the statistical independence of network parameters, can also lead to interacting theories. These other expansions can be advantageous over the $1/N$-expansion, for example by improved behavior with respect to the universal approximation theorem. Given the connected correlators of a field theory, one can systematically reconstruct the action order-by-order in the expansion parameter, using a new Feynman diagram prescription whose vertices are the connected correlators. This method is motivated by the Edgeworth expansion and allows one to derive actions for neural network field theories. Conversely, the correspondence allows one to engineer architectures realizing a given field theory by representing action deformations as deformations of neural network parameter densities. As an example, $\phi^4$ theory is realized as an infinite-$N$ neural network field theory.

Symmetry-via-Duality: Invariant Neural Network Densities from Parameter-Space Correlators

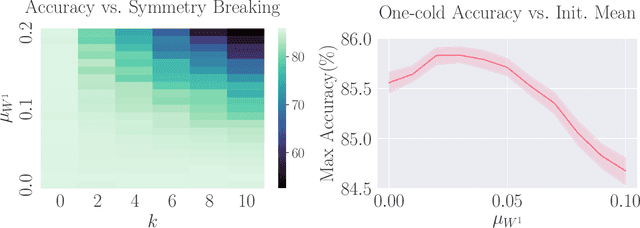
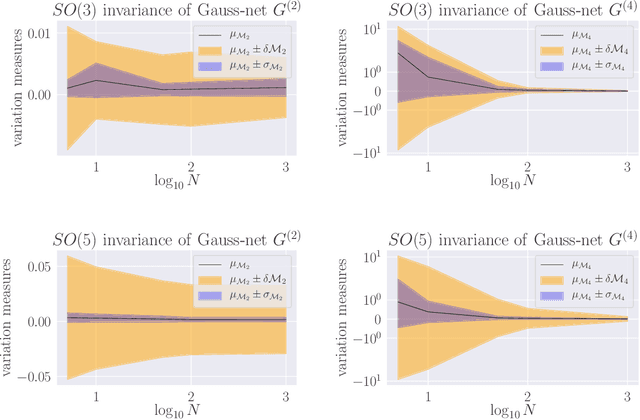
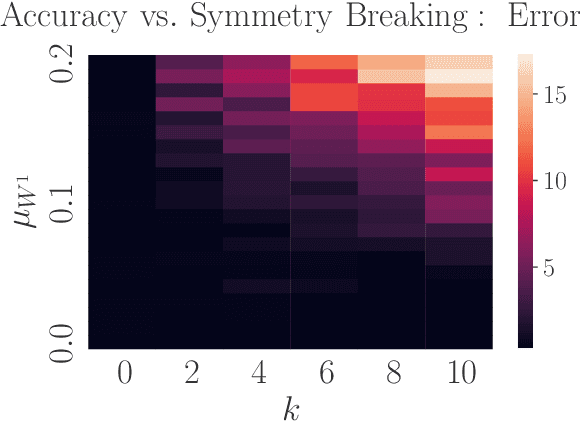
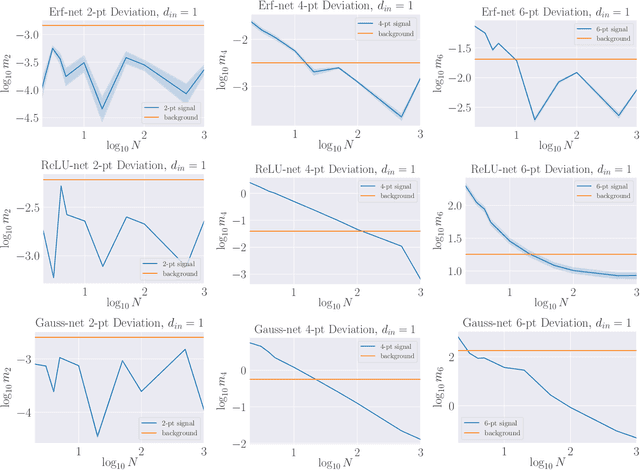
Parameter-space and function-space provide two different duality frames in which to study neural networks. We demonstrate that symmetries of network densities may be determined via dual computations of network correlation functions, even when the density is unknown and the network is not equivariant. Symmetry-via-duality relies on invariance properties of the correlation functions, which stem from the choice of network parameter distributions. Input and output symmetries of neural network densities are determined, which recover known Gaussian process results in the infinite width limit. The mechanism may also be utilized to determine symmetries during training, when parameters are correlated, as well as symmetries of the Neural Tangent Kernel. We demonstrate that the amount of symmetry in the initialization density affects the accuracy of networks trained on Fashion-MNIST, and that symmetry breaking helps only when it is in the direction of ground truth.

Neural Networks and Quantum Field Theory

We propose a theoretical understanding of neural networks in terms of Wilsonian effective field theory. The correspondence relies on the fact that many asymptotic neural networks are drawn from Gaussian processes, the analog of non-interacting field theories. Moving away from the asymptotic limit yields a non-Gaussian process and corresponds to turning on particle interactions, allowing for the computation of correlation functions of neural network outputs with Feynman diagrams. Minimal non-Gaussian process likelihoods are determined by the most relevant non-Gaussian terms, according to the flow in their coefficients induced by the Wilsonian renormalization group. This yields a direct connection between overparameterization and simplicity of neural network likelihoods. Whether the coefficients are constants or functions may be understood in terms of GP limit symmetries, as expected from 't Hooft's technical naturalness. General theoretical calculations are matched to neural network experiments in the simplest class of models allowing the correspondence. Our formalism is valid for any of the many architectures that becomes a GP in an asymptotic limit, a property preserved under certain types of training.