Exploring the Energy Landscape of RBMs: Reciprocal Space Insights into Bosons, Hierarchical Learning and Symmetry Breaking

Deep generative models have become ubiquitous due to their ability to learn and sample from complex distributions. Despite the proliferation of various frameworks, the relationships among these models remain largely unexplored, a gap that hinders the development of a unified theory of AI learning. We address two central challenges: clarifying the connections between different deep generative models and deepening our understanding of their learning mechanisms. We focus on Restricted Boltzmann Machines (RBMs), known for their universal approximation capabilities for discrete distributions. By introducing a reciprocal space formulation, we reveal a connection between RBMs, diffusion processes, and coupled Bosons. We show that at initialization, the RBM operates at a saddle point, where the local curvature is determined by the singular values, whose distribution follows the Marcenko-Pastur law and exhibits rotational symmetry. During training, this rotational symmetry is broken due to hierarchical learning, where different degrees of freedom progressively capture features at multiple levels of abstraction. This leads to a symmetry breaking in the energy landscape, reminiscent of Landau theory. This symmetry breaking in the energy landscape is characterized by the singular values and the weight matrix eigenvector matrix. We derive the corresponding free energy in a mean-field approximation. We show that in the limit of infinite size RBM, the reciprocal variables are Gaussian distributed. Our findings indicate that in this regime, there will be some modes for which the diffusion process will not converge to the Boltzmann distribution. To illustrate our results, we trained replicas of RBMs with different hidden layer sizes using the MNIST dataset. Our findings bridge the gap between disparate generative frameworks and also shed light on the processes underpinning learning in generative models.

Autoregressive model path dependence near Ising criticality

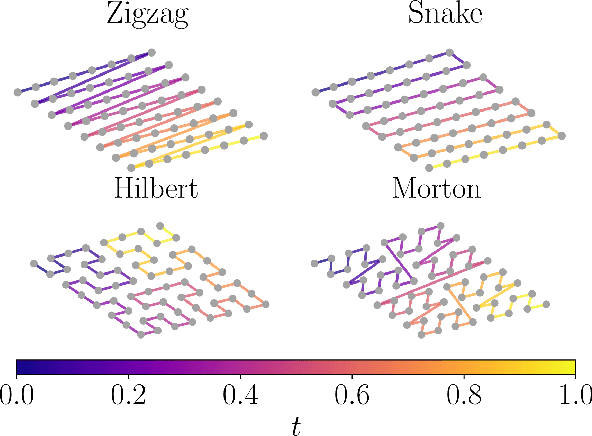
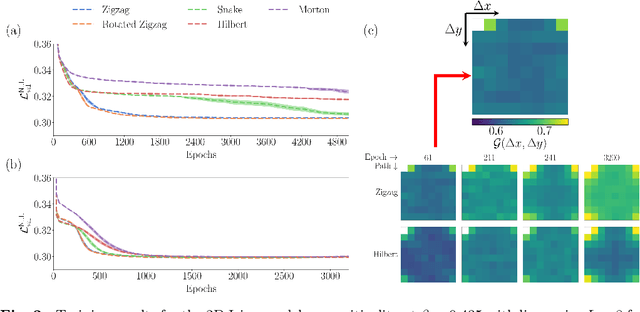
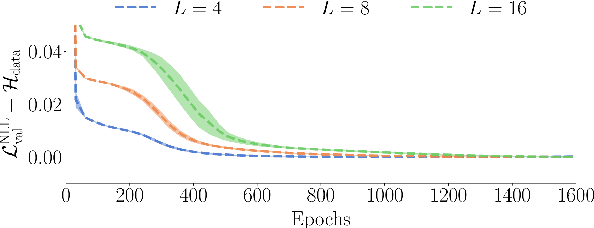
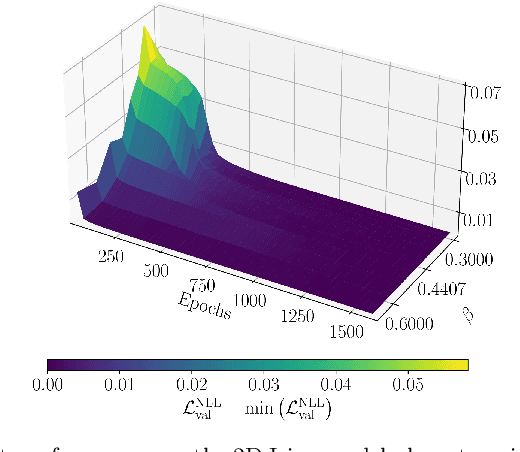
Autoregressive models are a class of generative model that probabilistically predict the next output of a sequence based on previous inputs. The autoregressive sequence is by definition one-dimensional (1D), which is natural for language tasks and hence an important component of modern architectures like recurrent neural networks (RNNs) and transformers. However, when language models are used to predict outputs on physical systems that are not intrinsically 1D, the question arises of which choice of autoregressive sequence -- if any -- is optimal. In this paper, we study the reconstruction of critical correlations in the two-dimensional (2D) Ising model, using RNNs and transformers trained on binary spin data obtained near the thermal phase transition. We compare the training performance for a number of different 1D autoregressive sequences imposed on finite-size 2D lattices. We find that paths with long 1D segments are more efficient at training the autoregressive models compared to space-filling curves that better preserve the 2D locality. Our results illustrate the potential importance in choosing the optimal autoregressive sequence ordering when training modern language models for tasks in physics.

Robust quantum dots charge autotuning using neural networks uncertainty

This study presents a machine-learning-based procedure to automate the charge tuning of semiconductor spin qubits with minimal human intervention, addressing one of the significant challenges in scaling up quantum dot technologies. This method exploits artificial neural networks to identify noisy transition lines in stability diagrams, guiding a robust exploration strategy leveraging neural networks' uncertainty estimations. Tested across three distinct offline experimental datasets representing different single quantum dot technologies, the approach achieves over 99% tuning success rate in optimal cases, where more than 10% of the success is directly attributable to uncertainty exploitation. The challenging constraints of small training sets containing high diagram-to-diagram variability allowed us to evaluate the capabilities and limits of the proposed procedure.

CaloQVAE : Simulating high-energy particle-calorimeter interactions using hybrid quantum-classical generative models

The Large Hadron Collider's high luminosity era presents major computational challenges in the analysis of collision events. Large amounts of Monte Carlo (MC) simulation will be required to constrain the statistical uncertainties of the simulated datasets below these of the experimental data. Modelling of high-energy particles propagating through the calorimeter section of the detector is the most computationally intensive MC simulation task. We introduce a technique combining recent advancements in generative models and quantum annealing for fast and efficient simulation of high-energy particle-calorimeter interactions.

Investigating Topological Order using Recurrent Neural Networks

Recurrent neural networks (RNNs), originally developed for natural language processing, hold great promise for accurately describing strongly correlated quantum many-body systems. Here, we employ 2D RNNs to investigate two prototypical quantum many-body Hamiltonians exhibiting topological order. Specifically, we demonstrate that RNN wave functions can effectively capture the topological order of the toric code and a Bose-Hubbard spin liquid on the kagome lattice by estimating their topological entanglement entropies. We also find that RNNs favor coherent superpositions of minimally-entangled states over minimally-entangled states themselves. Overall, our findings demonstrate that RNN wave functions constitute a powerful tool to study phases of matter beyond Landau's symmetry-breaking paradigm.

Supplementing Recurrent Neural Network Wave Functions with Symmetry and Annealing to Improve Accuracy

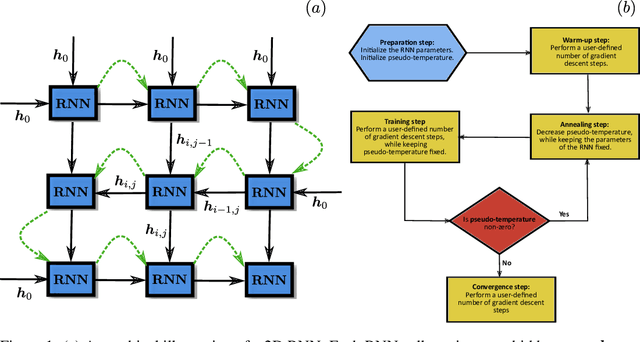
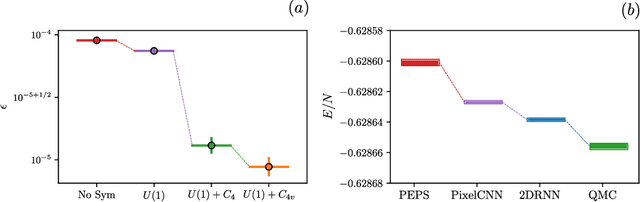
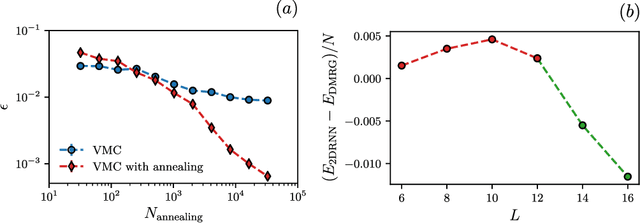
Recurrent neural networks (RNNs) are a class of neural networks that have emerged from the paradigm of artificial intelligence and has enabled lots of interesting advances in the field of natural language processing. Interestingly, these architectures were shown to be powerful ansatze to approximate the ground state of quantum systems. Here, we build over the results of [Phys. Rev. Research 2, 023358 (2020)] and construct a more powerful RNN wave function ansatz in two dimensions. We use symmetry and annealing to obtain accurate estimates of ground state energies of the two-dimensional (2D) Heisenberg model, on the square lattice and on the triangular lattice. We show that our method is superior to Density Matrix Renormalisation Group (DMRG) for system sizes larger than or equal to $14 \times 14$ on the triangular lattice.

Twin Neural Network Regression is a Semi-Supervised Regression Algorithm

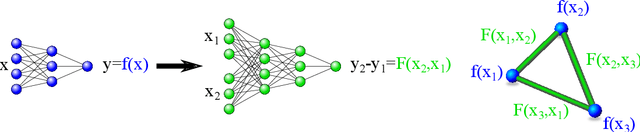
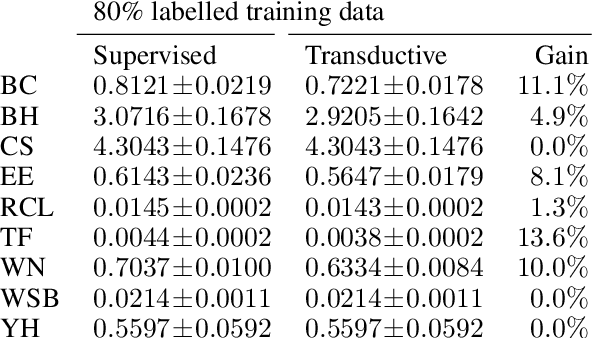
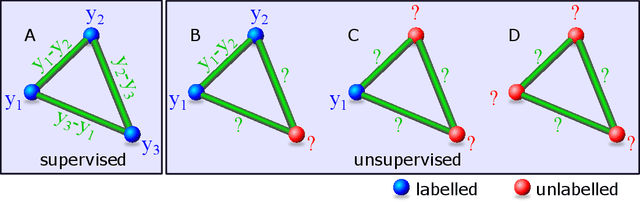
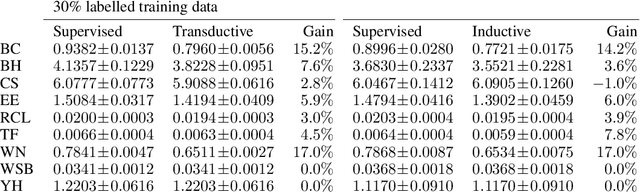
Twin neural network regression (TNNR) is a semi-supervised regression algorithm, it can be trained on unlabelled data points as long as other, labelled anchor data points, are present. TNNR is trained to predict differences between the target values of two different data points rather than the targets themselves. By ensembling predicted differences between the targets of an unseen data point and all training data points, it is possible to obtain a very accurate prediction for the original regression problem. Since any loop of predicted differences should sum to zero, loops can be supplied to the training data, even if the data points themselves within loops are unlabelled. Semi-supervised training improves TNNR performance, which is already state of the art, significantly.

Variational Neural Annealing

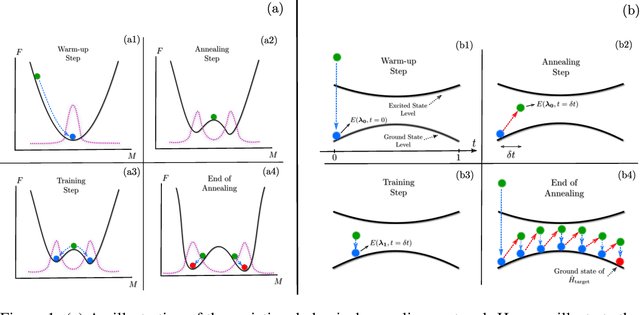
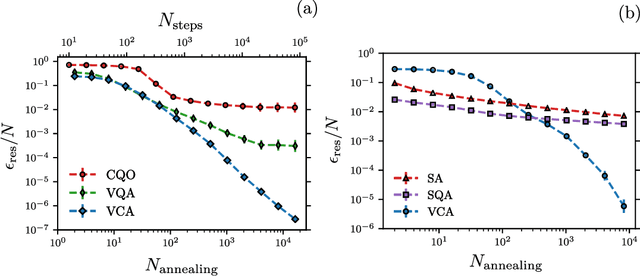
Many important challenges in science and technology can be cast as optimization problems. When viewed in a statistical physics framework, these can be tackled by simulated annealing, where a gradual cooling procedure helps search for groundstate solutions of a target Hamiltonian. While powerful, simulated annealing is known to have prohibitively slow sampling dynamics when the optimization landscape is rough or glassy. Here we show that by generalizing the target distribution with a parameterized model, an analogous annealing framework based on the variational principle can be used to search for groundstate solutions. Modern autoregressive models such as recurrent neural networks provide ideal parameterizations since they can be exactly sampled without slow dynamics even when the model encodes a rough landscape. We implement this procedure in the classical and quantum settings on several prototypical spin glass Hamiltonians, and find that it significantly outperforms traditional simulated annealing in the asymptotic limit, illustrating the potential power of this yet unexplored route to optimization.

Twin Neural Network Regression

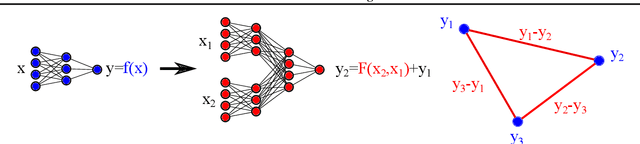
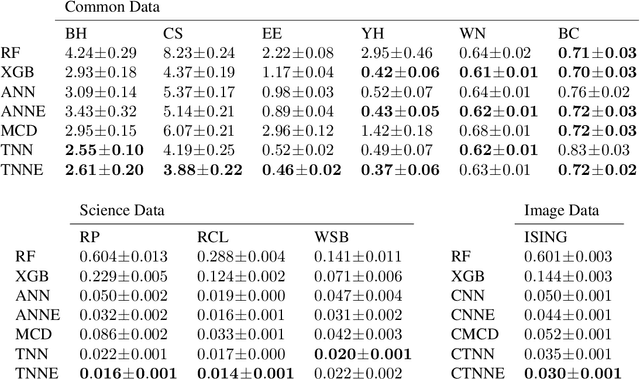
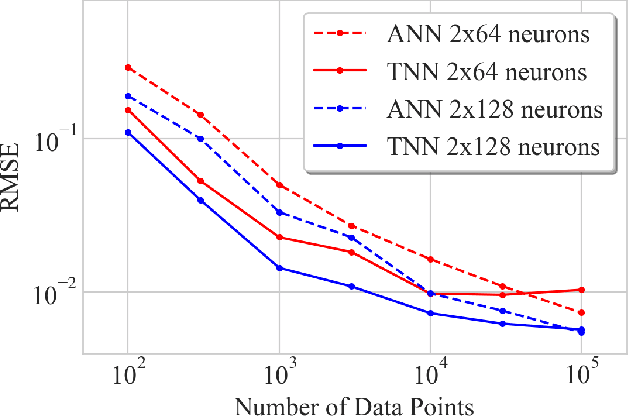
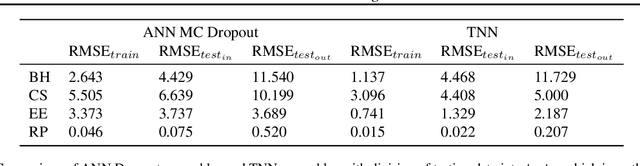
We introduce twin neural network (TNN) regression. This method predicts differences between the target values of two different data points rather than the targets themselves. The solution of a traditional regression problem is then obtained by averaging over an ensemble of all predicted differences between the targets of an unseen data point and all training data points. Whereas ensembles are normally costly to produce, TNN regression intrinsically creates an ensemble of predictions of twice the size of the training set while only training a single neural network. Since ensembles have been shown to be more accurate than single models this property naturally transfers to TNN regression. We show that TNNs are able to compete or yield more accurate predictions for different data sets, compared to other state-of-the-art methods. Furthermore, TNN regression is constrained by self-consistency conditions. We find that the violation of these conditions provides an estimate for the prediction uncertainty.

Discovering Symmetry Invariants and Conserved Quantities by Interpreting Siamese Neural Networks

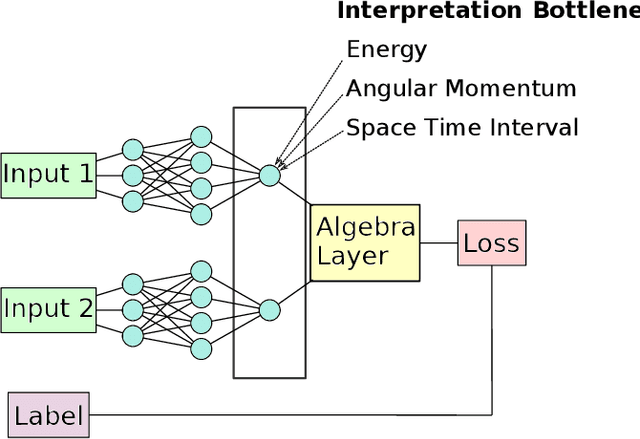
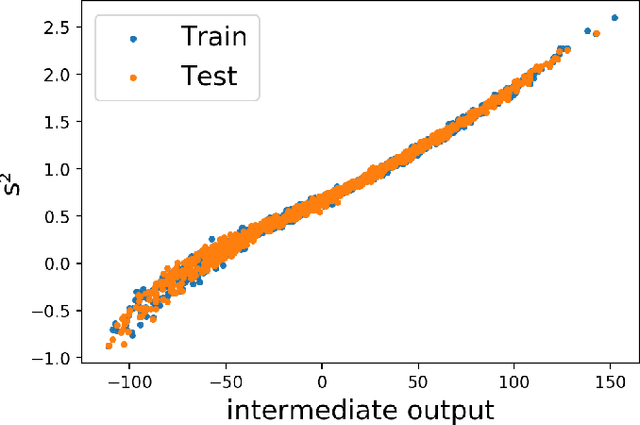
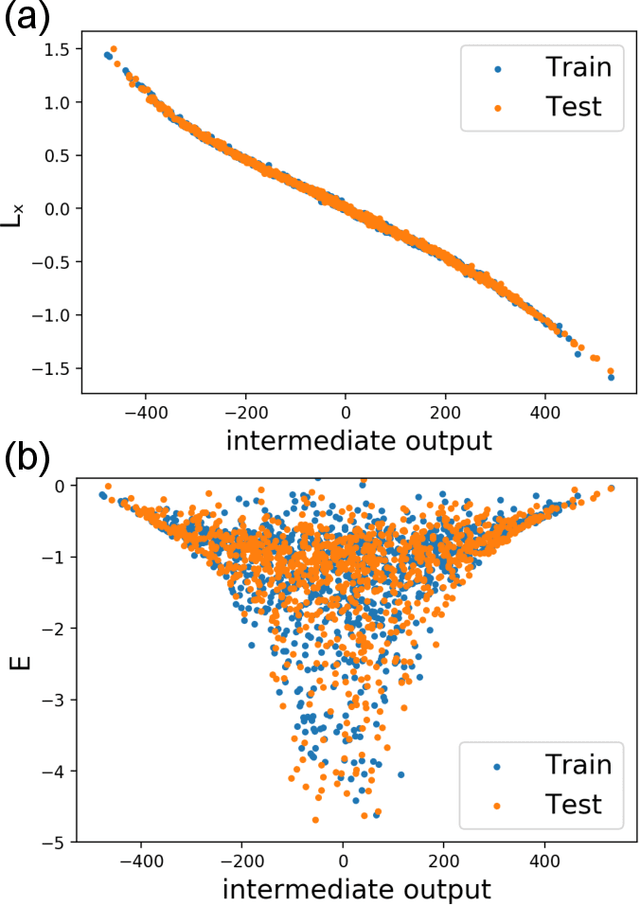
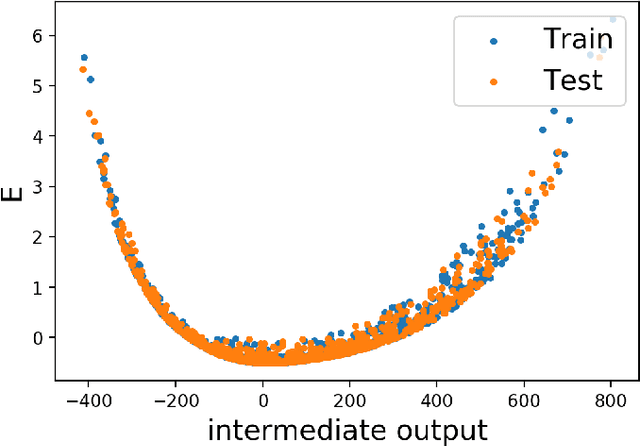
In this paper, we introduce interpretable Siamese Neural Networks (SNN) for similarity detection to the field of theoretical physics. More precisely, we apply SNNs to events in special relativity, the transformation of electromagnetic fields, and the motion of particles in a central potential. In these examples, the SNNs learn to identify datapoints belonging to the same events, field configurations, or trajectory of motion. It turns out that in the process of learning which datapoints belong to the same event or field configuration, these SNNs also learn the relevant symmetry invariants and conserved quantities. These SNNs are highly interpretable, which enables us to reveal the symmetry invariants and conserved quantities without prior knowledge.