BertRLFuzzer: A BERT and Reinforcement Learning based Fuzzer

We present a novel tool BertRLFuzzer, a BERT and Reinforcement Learning (RL) based fuzzer aimed at finding security vulnerabilities. BertRLFuzzer works as follows: given a list of seed inputs, the fuzzer performs grammar-adhering and attack-provoking mutation operations on them to generate candidate attack vectors. The key insight of BertRLFuzzer is the combined use of two machine learning concepts. The first one is the use of semi-supervised learning with language models (e.g., BERT) that enables BertRLFuzzer to learn (relevant fragments of) the grammar of a victim application as well as attack patterns, without requiring the user to specify it explicitly. The second one is the use of RL with BERT model as an agent to guide the fuzzer to efficiently learn grammar-adhering and attack-provoking mutation operators. The RL-guided feedback loop enables BertRLFuzzer to automatically search the space of attack vectors to exploit the weaknesses of the given victim application without the need to create labeled training data. Furthermore, these two features together enable BertRLFuzzer to be extensible, i.e., the user can extend BertRLFuzzer to a variety of victim applications and attack vectors automatically (i.e., without explicitly modifying the fuzzer or providing a grammar). In order to establish the efficacy of BertRLFuzzer we compare it against a total of 13 black box and white box fuzzers over a benchmark of 9 victim websites. We observed a significant improvement in terms of time to first attack (54% less than the nearest competing tool), time to find all vulnerabilities (40-60% less than the nearest competing tool), and attack rate (4.4% more attack vectors generated than the nearest competing tool). Our experiments show that the combination of the BERT model and RL-based learning makes BertRLFuzzer an effective, adaptive, easy-to-use, automatic, and extensible fuzzer.

Logic Guided Genetic Algorithms

We present a novel Auxiliary Truth enhanced Genetic Algorithm (GA) that uses logical or mathematical constraints as a means of data augmentation as well as to compute loss (in conjunction with the traditional MSE), with the aim of increasing both data efficiency and accuracy of symbolic regression (SR) algorithms. Our method, logic-guided genetic algorithm (LGGA), takes as input a set of labelled data points and auxiliary truths (ATs) (mathematical facts known a priori about the unknown function the regressor aims to learn) and outputs a specially generated and curated dataset that can be used with any SR method. Three key insights underpin our method: first, SR users often know simple ATs about the function they are trying to learn. Second, whenever an SR system produces a candidate equation inconsistent with these ATs, we can compute a counterexample to prove the inconsistency, and further, this counterexample may be used to augment the dataset and fed back to the SR system in a corrective feedback loop. Third, the value addition of these ATs is that their use in both the loss function and the data augmentation process leads to better rates of convergence, accuracy, and data efficiency. We evaluate LGGA against state-of-the-art SR tools, namely, Eureqa and TuringBot on 16 physics equations from "The Feynman Lectures on Physics" book. We find that using these SR tools in conjunction with LGGA results in them solving up to 30.0% more equations, needing only a fraction of the amount of data compared to the same tool without LGGA, i.e., resulting in up to a 61.9% improvement in data efficiency.

LGML: Logic Guided Machine Learning

We introduce Logic Guided Machine Learning (LGML), a novel approach that symbiotically combines machine learning (ML) and logic solvers with the goal of learning mathematical functions from data. LGML consists of two phases, namely a learning-phase and a logic-phase with a corrective feedback loop, such that, the learning-phase learns symbolic expressions from input data, and the logic-phase cross verifies the consistency of the learned expression with known auxiliary truths. If inconsistent, the logic-phase feeds back "counterexamples" to the learning-phase. This process is repeated until the learned expression is consistent with auxiliary truth. Using LGML, we were able to learn expressions that correspond to the Pythagorean theorem and the sine function, with several orders of magnitude improvements in data efficiency compared to an approach based on an out-of-the-box multi-layered perceptron (MLP).

Discovering Symmetry Invariants and Conserved Quantities by Interpreting Siamese Neural Networks

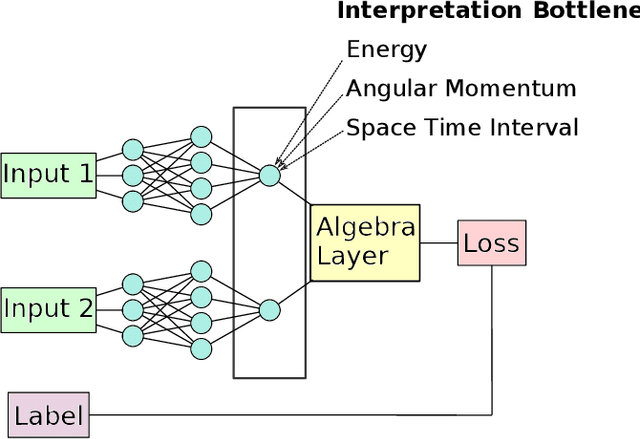
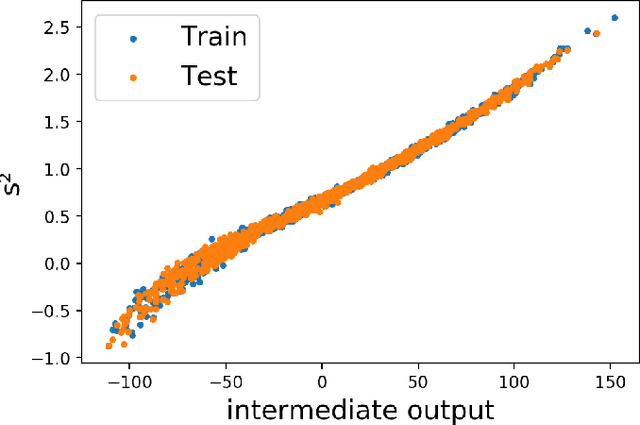
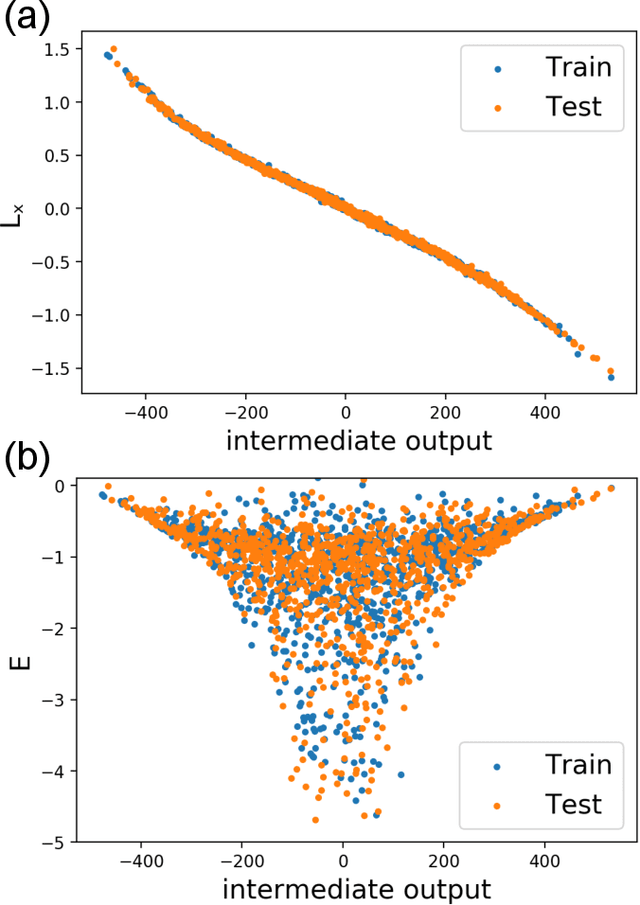
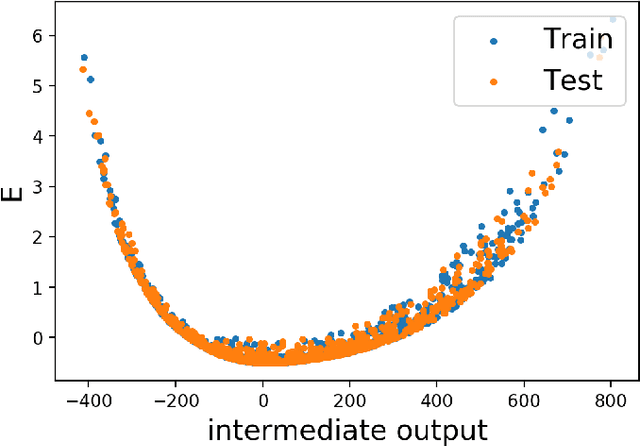
In this paper, we introduce interpretable Siamese Neural Networks (SNN) for similarity detection to the field of theoretical physics. More precisely, we apply SNNs to events in special relativity, the transformation of electromagnetic fields, and the motion of particles in a central potential. In these examples, the SNNs learn to identify datapoints belonging to the same events, field configurations, or trajectory of motion. It turns out that in the process of learning which datapoints belong to the same event or field configuration, these SNNs also learn the relevant symmetry invariants and conserved quantities. These SNNs are highly interpretable, which enables us to reveal the symmetry invariants and conserved quantities without prior knowledge.

LogicGAN: Logic-guided Generative Adversarial Networks

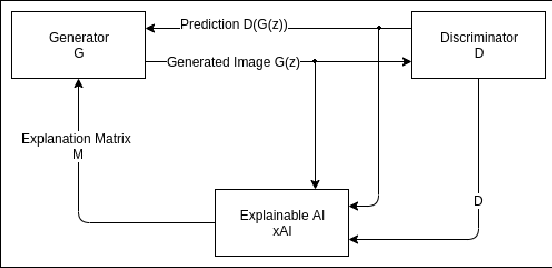
Generative Adversarial Networks (GANs) are a revolutionary class of Deep Neural Networks (DNNs) that have been successfully used to generate realistic images, music, text, and other data. However, it is well known that GAN training can be notoriously resource-intensive and presents many challenges. Further, a potential weakness in GANs is that discriminator DNNs typically provide only one value (loss) of corrective feedback to generator DNNs (namely, the discriminator's assessment of the generated example). By contrast, we propose a new class of GAN we refer to as LogicGAN, that leverages recent advances in (logic-based) explainable AI (xAI) systems to provide a "richer" form of corrective feedback from discriminators to generators. Specifically, we modify the gradient descent process using xAI systems that specify the reason as to why the discriminator made the classification it did, thus providing the richer corrective feedback that helps the generator to better fool the discriminator. Using our approach, we show that LogicGANs learn much faster on MNIST data, achieving an improvement in data efficiency of 45% in single and 12.73% in multi-class setting over standard GANs while maintaining the same quality as measured by Fr\'echet Inception Distance. Further, we argue that LogicGAN enables users greater control over how models learn than standard GAN systems.