Twin Neural Network Improved k-Nearest Neighbor Regression

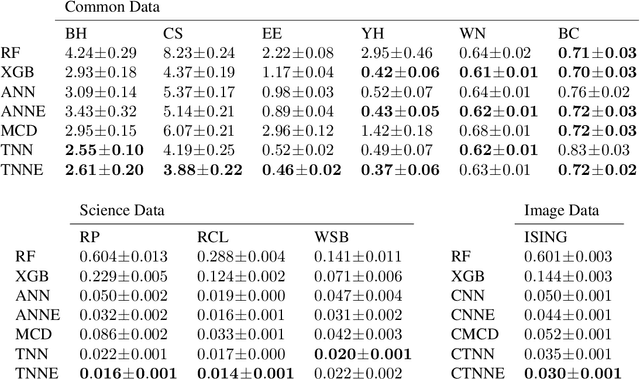
Twin neural network regression is trained to predict differences between regression targets rather than the targets themselves. A solution to the original regression problem can be obtained by ensembling predicted differences between the targets of an unknown data point and multiple known anchor data points. Choosing the anchors to be the nearest neighbors of the unknown data point leads to a neural network-based improvement of k-nearest neighbor regression. This algorithm is shown to outperform both neural networks and k-nearest neighbor regression on small to medium-sized data sets.

How to get the most out of Twinned Regression Methods

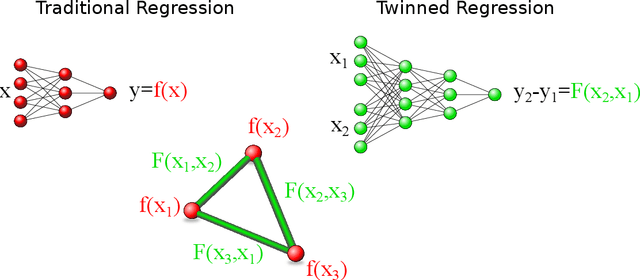
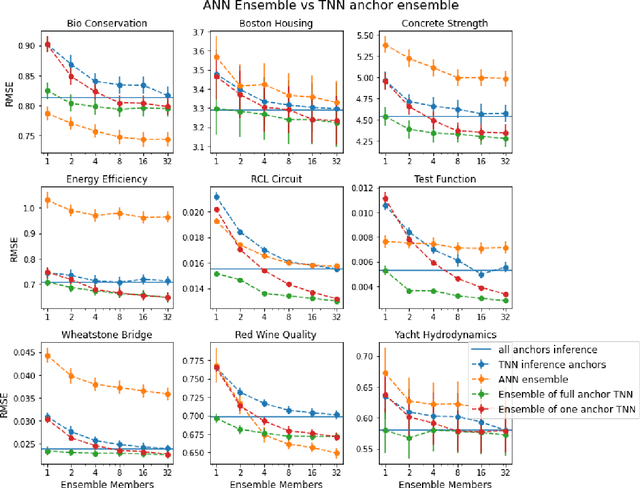
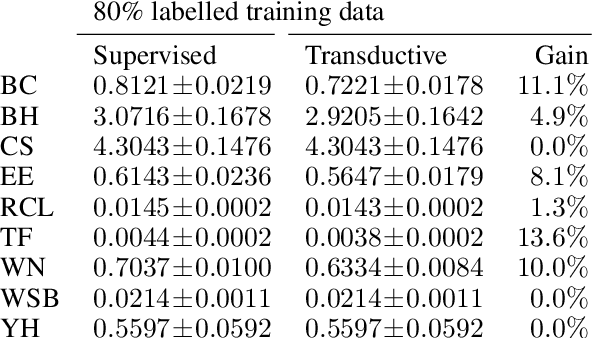
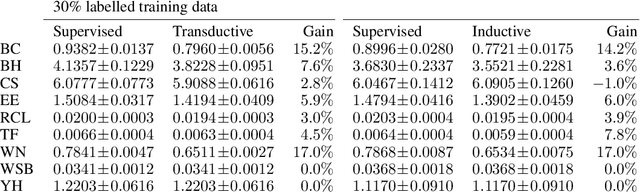
Twinned regression methods are designed to solve the dual problem to the original regression problem, predicting differences between regression targets rather then the targets themselves. A solution to the original regression problem can be obtained by ensembling predicted differences between the targets of an unknown data point and multiple known anchor data points. We explore different aspects of twinned regression methods: (1) We decompose different steps in twinned regression algorithms and examine their contributions to the final performance, (2) We examine the intrinsic ensemble quality, (3) We combine twin neural network regression with k-nearest neighbor regression to design a more accurate and efficient regression method, and (4) we develop a simplified semi-supervised regression scheme.

Unsupervised Learning of Rydberg Atom Array Phase Diagram with Siamese Neural Networks

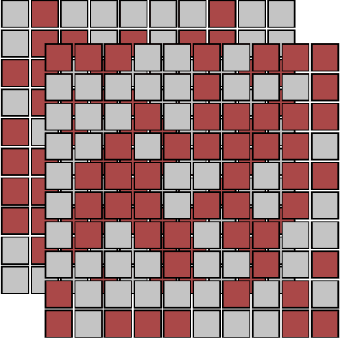
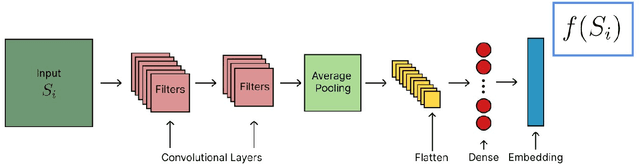
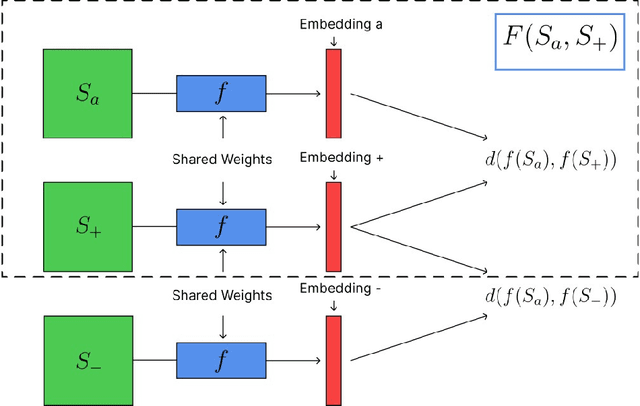
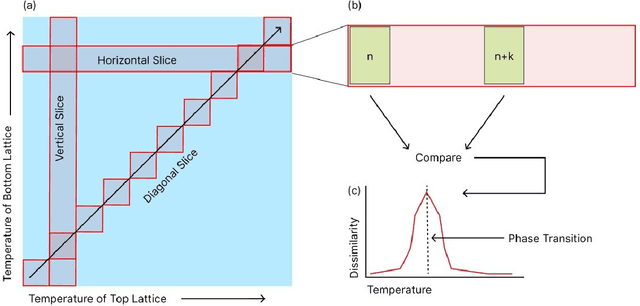
We introduce an unsupervised machine learning method based on Siamese Neural Networks (SNN) to detect phase boundaries. This method is applied to Monte-Carlo simulations of Ising-type systems and Rydberg atom arrays. In both cases the SNN reveals phase boundaries consistent with prior research. The combination of leveraging the power of feed-forward neural networks, unsupervised learning and the ability to learn about multiple phases without knowing about their existence provides a powerful method to explore new and unknown phases of matter.

Twin Neural Network Regression is a Semi-Supervised Regression Algorithm

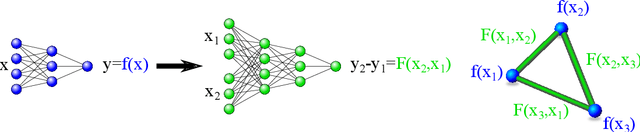
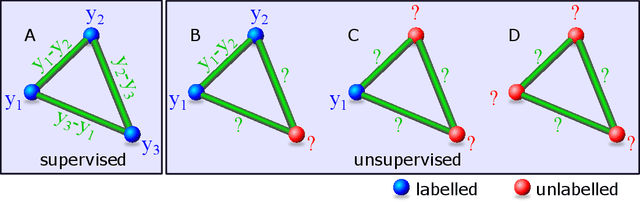
Twin neural network regression (TNNR) is a semi-supervised regression algorithm, it can be trained on unlabelled data points as long as other, labelled anchor data points, are present. TNNR is trained to predict differences between the target values of two different data points rather than the targets themselves. By ensembling predicted differences between the targets of an unseen data point and all training data points, it is possible to obtain a very accurate prediction for the original regression problem. Since any loop of predicted differences should sum to zero, loops can be supplied to the training data, even if the data points themselves within loops are unlabelled. Semi-supervised training improves TNNR performance, which is already state of the art, significantly.

Twin Neural Network Regression

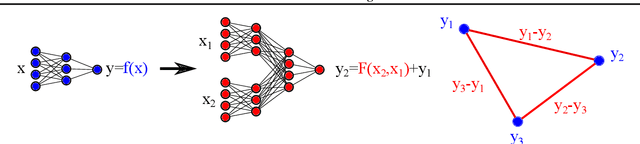
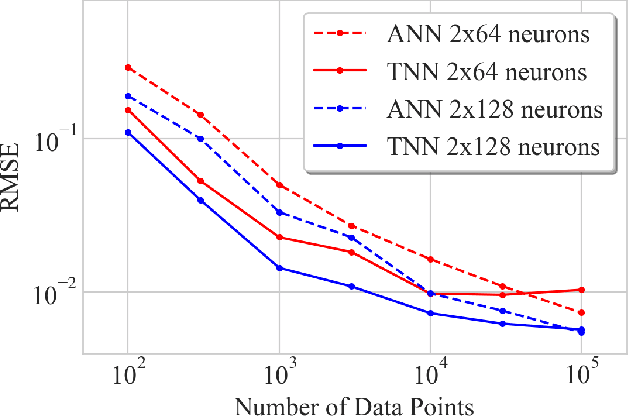
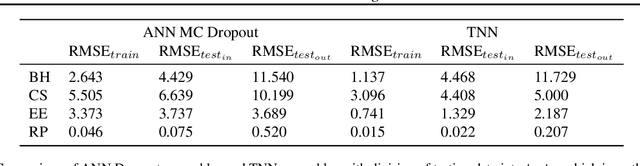
We introduce twin neural network (TNN) regression. This method predicts differences between the target values of two different data points rather than the targets themselves. The solution of a traditional regression problem is then obtained by averaging over an ensemble of all predicted differences between the targets of an unseen data point and all training data points. Whereas ensembles are normally costly to produce, TNN regression intrinsically creates an ensemble of predictions of twice the size of the training set while only training a single neural network. Since ensembles have been shown to be more accurate than single models this property naturally transfers to TNN regression. We show that TNNs are able to compete or yield more accurate predictions for different data sets, compared to other state-of-the-art methods. Furthermore, TNN regression is constrained by self-consistency conditions. We find that the violation of these conditions provides an estimate for the prediction uncertainty.

Discovering Symmetry Invariants and Conserved Quantities by Interpreting Siamese Neural Networks

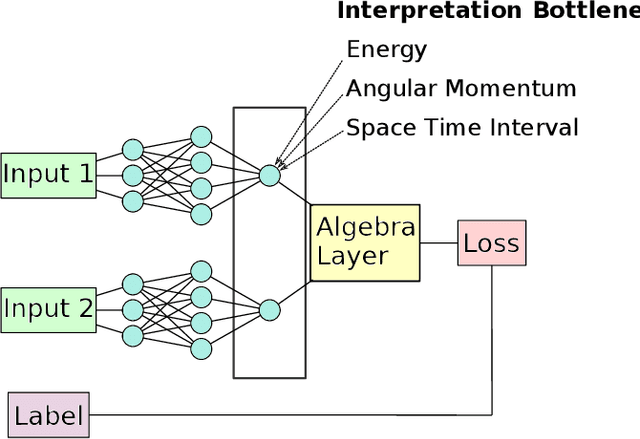
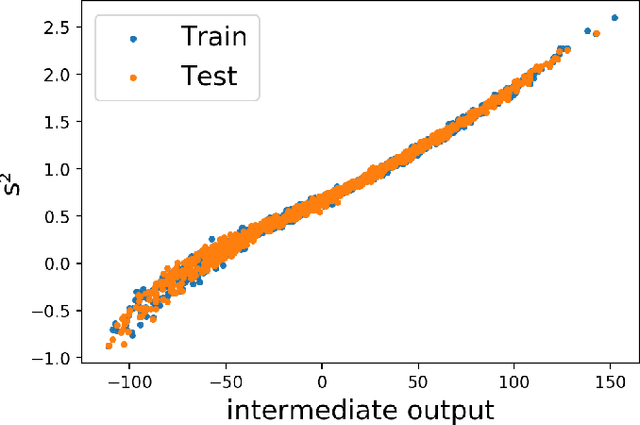
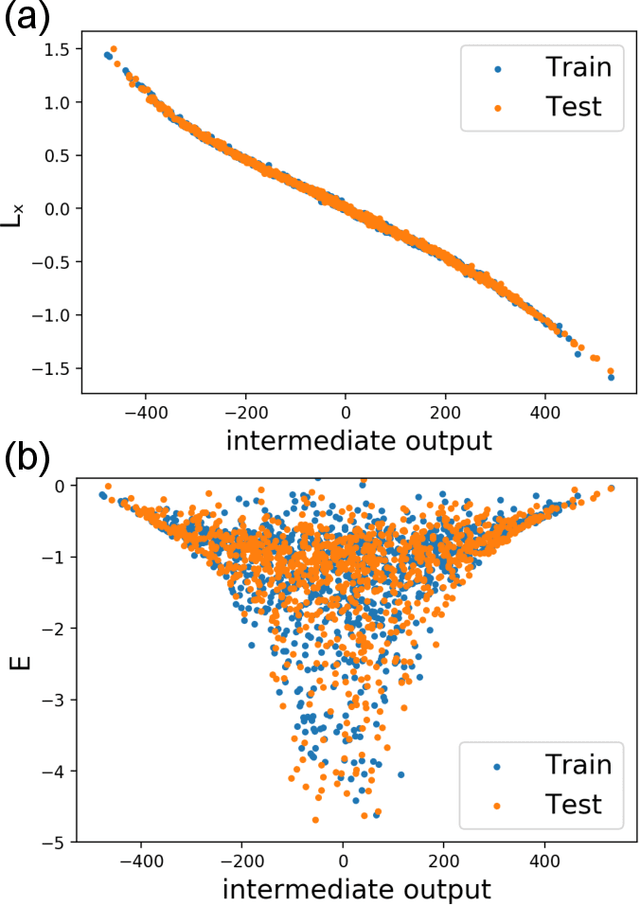
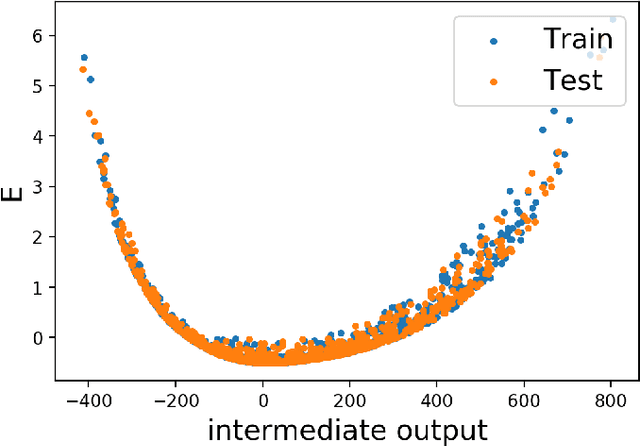
In this paper, we introduce interpretable Siamese Neural Networks (SNN) for similarity detection to the field of theoretical physics. More precisely, we apply SNNs to events in special relativity, the transformation of electromagnetic fields, and the motion of particles in a central potential. In these examples, the SNNs learn to identify datapoints belonging to the same events, field configurations, or trajectory of motion. It turns out that in the process of learning which datapoints belong to the same event or field configuration, these SNNs also learn the relevant symmetry invariants and conserved quantities. These SNNs are highly interpretable, which enables us to reveal the symmetry invariants and conserved quantities without prior knowledge.

Spectral Reconstruction with Deep Neural Networks

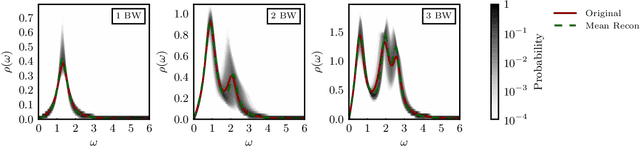
We explore artificial neural networks as a tool for the reconstruction of spectral functions from imaginary time Green's functions, a classic ill-conditioned inverse problem. Our ansatz is based on a supervised learning framework in which prior knowledge is encoded in the training data and the inverse transformation manifold is explicitly parametrised through a neural network. We systematically investigate this novel reconstruction approach, providing a detailed analysis of its performance on physically motivated mock data, and compare it to established methods of Bayesian inference. The reconstruction accuracy is found to be at least comparable, and potentially superior in particular at larger noise levels. We argue that the use of labelled training data in a supervised setting and the freedom in defining an optimisation objective are inherent advantages of the present approach and may lead to significant improvements over state-of-the-art methods in the future. Potential directions for further research are discussed in detail.