Flow-based density of states for complex actions

Emerging sampling algorithms based on normalizing flows have the potential to solve ergodicity problems in lattice calculations. Furthermore, it has been noted that flows can be used to compute thermodynamic quantities which are difficult to access with traditional methods. This suggests that they are also applicable to the density-of-states approach to complex action problems. In particular, flow-based sampling may be used to compute the density directly, in contradistinction to the conventional strategy of reconstructing it via measuring and integrating the derivative of its logarithm. By circumventing this procedure, the accumulation of errors from the numerical integration is avoided completely and the overall normalization factor can be determined explicitly. In this proof-of-principle study, we demonstrate our method in the context of two-component scalar field theory where the $O(2)$ symmetry is explicitly broken by an imaginary external field. First, we concentrate on the zero-dimensional case which can be solved exactly. We show that with our method, the Lee-Yang zeroes of the associated partition function can be successfully located. Subsequently, we confirm that the flow-based approach correctly reproduces the density computed with conventional methods in one- and two-dimensional models.

Spiking neuromorphic chip learns entangled quantum states

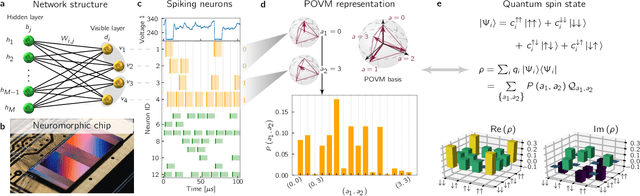
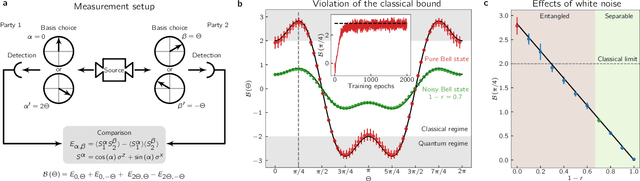
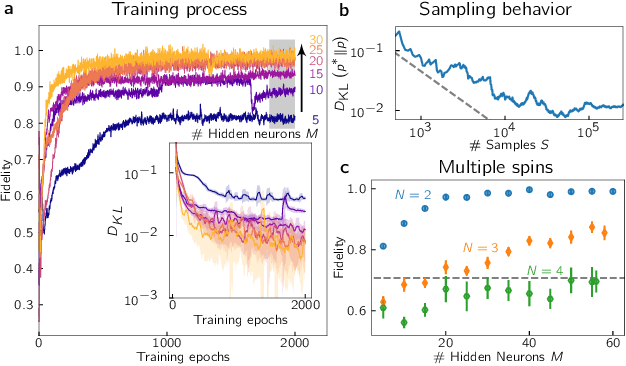
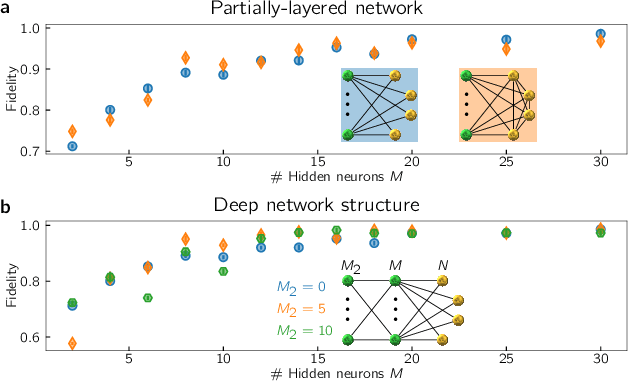
Neuromorphic systems are designed to emulate certain structural and dynamical properties of biological neuronal networks, with the aim of inheriting the brain's functional performance and energy efficiency in artificial-intelligence applications [1,2]. Among the platforms existing today, the spike-based BrainScaleS system stands out by realizing fast analog dynamics which can boost computationally expensive tasks [3]. Here we use the latest BrainScaleS generation [4] for the algorithm-free simulation of quantum systems, thereby opening up an entirely new application space for these devices. This requires an appropriate spike-based representation of quantum states and an associated training method for imprinting a desired target state onto the network. We employ a representation of quantum states using probability distributions [5,6], enabling the use of a Bayesian sampling framework for spiking neurons [7]. For training, we developed a Hebbian learning scheme that explicitly exploits the inherent speed of the substrate, which enables us to realize a variety of network topologies. We encoded maximally entangled states of up to four qubits and observed fidelities that imply genuine $N$-partite entanglement. In particular, the encoding of entangled pure and mixed two-qubit states reaches a quality that allows the observation of Bell correlations, thus demonstrating that non-classical features of quantum systems can be captured by spiking neural dynamics. Our work establishes an intriguing connection between quantum systems and classical spiking networks, and demonstrates the feasibility of simulating quantum systems with neuromorphic hardware.

Towards Novel Insights in Lattice Field Theory with Explainable Machine Learning

Machine learning has the potential to aid our understanding of phase structures in lattice quantum field theories through the statistical analysis of Monte Carlo samples. Available algorithms, in particular those based on deep learning, often demonstrate remarkable performance in the search for previously unidentified features, but tend to lack transparency if applied naively. To address these shortcomings, we propose representation learning in combination with interpretability methods as a framework for the identification of observables. More specifically, we investigate action parameter regression as a pretext task while using layer-wise relevance propagation (LRP) to identify the most important observables depending on the location in the phase diagram. The approach is put to work in the context of a scalar Yukawa model in (2+1)d. First, we investigate a multilayer perceptron to determine an importance hierarchy of several predefined, standard observables. The method is then applied directly to the raw field configurations using a convolutional network, demonstrating the ability to reconstruct all order parameters from the learned filter weights. Based on our results, we argue that due to its broad applicability, attribution methods such as LRP could prove a useful and versatile tool in our search for new physical insights. In the case of the Yukawa model, it facilitates the construction of an observable that characterises the symmetric phase.

Spectral Reconstruction with Deep Neural Networks

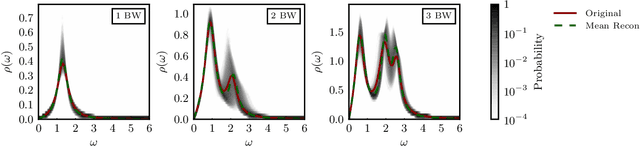
We explore artificial neural networks as a tool for the reconstruction of spectral functions from imaginary time Green's functions, a classic ill-conditioned inverse problem. Our ansatz is based on a supervised learning framework in which prior knowledge is encoded in the training data and the inverse transformation manifold is explicitly parametrised through a neural network. We systematically investigate this novel reconstruction approach, providing a detailed analysis of its performance on physically motivated mock data, and compare it to established methods of Bayesian inference. The reconstruction accuracy is found to be at least comparable, and potentially superior in particular at larger noise levels. We argue that the use of labelled training data in a supervised setting and the freedom in defining an optimisation objective are inherent advantages of the present approach and may lead to significant improvements over state-of-the-art methods in the future. Potential directions for further research are discussed in detail.

The Discrete Langevin Machine: Bridging the Gap Between Thermodynamic and Neuromorphic Systems

A formulation of Langevin dynamics for discrete systems is derived as a new class of generic stochastic processes. The dynamics simplify for a two-state system and suggest a novel network architecture which is implemented by the Langevin machine. The Langevin machine represents a promising approach to compute successfully quantitative exact results of Boltzmann distributed systems by LIF neurons. Besides a detailed introduction of the new dynamics, different simplified models of a neuromorphic hardware system are studied with respect to a control of emerging sources of errors.