Practical applications of machine-learned flows on gauge fields

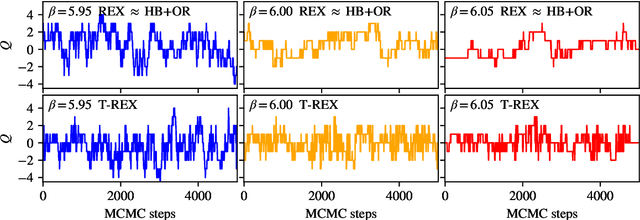
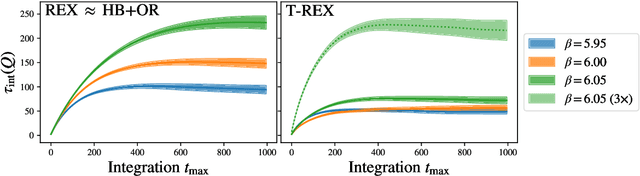
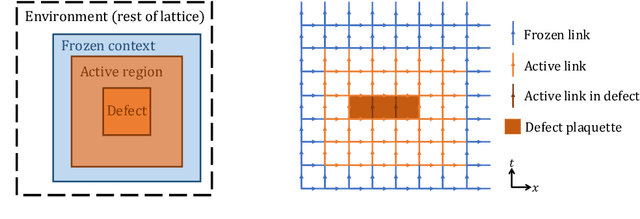
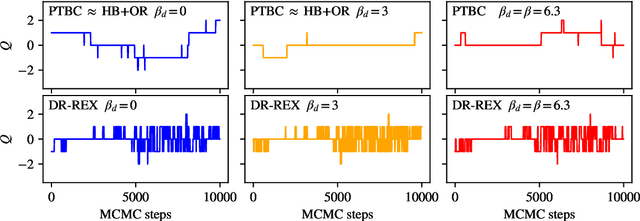
Normalizing flows are machine-learned maps between different lattice theories which can be used as components in exact sampling and inference schemes. Ongoing work yields increasingly expressive flows on gauge fields, but it remains an open question how flows can improve lattice QCD at state-of-the-art scales. We discuss and demonstrate two applications of flows in replica exchange (parallel tempering) sampling, aimed at improving topological mixing, which are viable with iterative improvements upon presently available flows.

Applications of flow models to the generation of correlated lattice QCD ensembles

Machine-learned normalizing flows can be used in the context of lattice quantum field theory to generate statistically correlated ensembles of lattice gauge fields at different action parameters. This work demonstrates how these correlations can be exploited for variance reduction in the computation of observables. Three different proof-of-concept applications are demonstrated using a novel residual flow architecture: continuum limits of gauge theories, the mass dependence of QCD observables, and hadronic matrix elements based on the Feynman-Hellmann approach. In all three cases, it is shown that statistical uncertainties are significantly reduced when machine-learned flows are incorporated as compared with the same calculations performed with uncorrelated ensembles or direct reweighting.

Normalizing flows for lattice gauge theory in arbitrary space-time dimension

Applications of normalizing flows to the sampling of field configurations in lattice gauge theory have so far been explored almost exclusively in two space-time dimensions. We report new algorithmic developments of gauge-equivariant flow architectures facilitating the generalization to higher-dimensional lattice geometries. Specifically, we discuss masked autoregressive transformations with tractable and unbiased Jacobian determinants, a key ingredient for scalable and asymptotically exact flow-based sampling algorithms. For concreteness, results from a proof-of-principle application to SU(3) lattice gauge theory in four space-time dimensions are reported.

Aspects of scaling and scalability for flow-based sampling of lattice QCD

Recent applications of machine-learned normalizing flows to sampling in lattice field theory suggest that such methods may be able to mitigate critical slowing down and topological freezing. However, these demonstrations have been at the scale of toy models, and it remains to be determined whether they can be applied to state-of-the-art lattice quantum chromodynamics calculations. Assessing the viability of sampling algorithms for lattice field theory at scale has traditionally been accomplished using simple cost scaling laws, but as we discuss in this work, their utility is limited for flow-based approaches. We conclude that flow-based approaches to sampling are better thought of as a broad family of algorithms with different scaling properties, and that scalability must be assessed experimentally.

Gauge-equivariant flow models for sampling in lattice field theories with pseudofermions

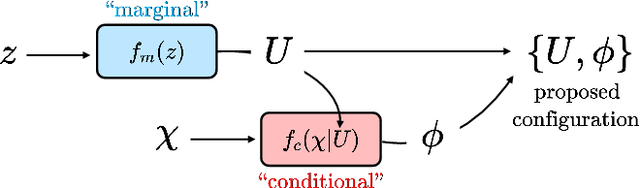
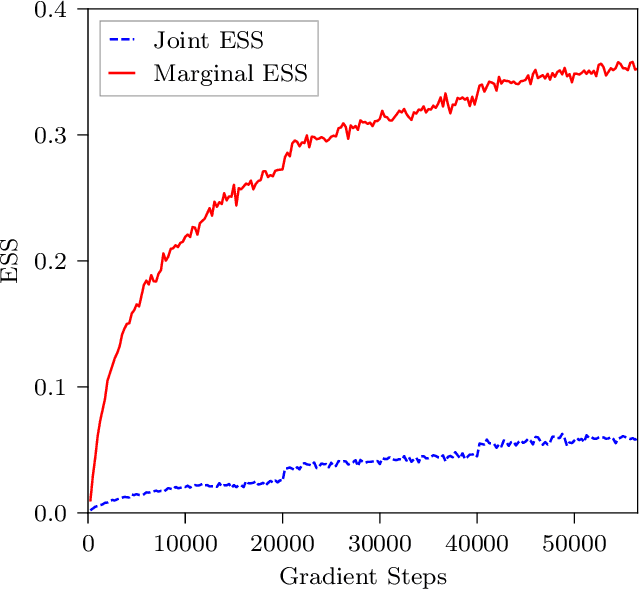
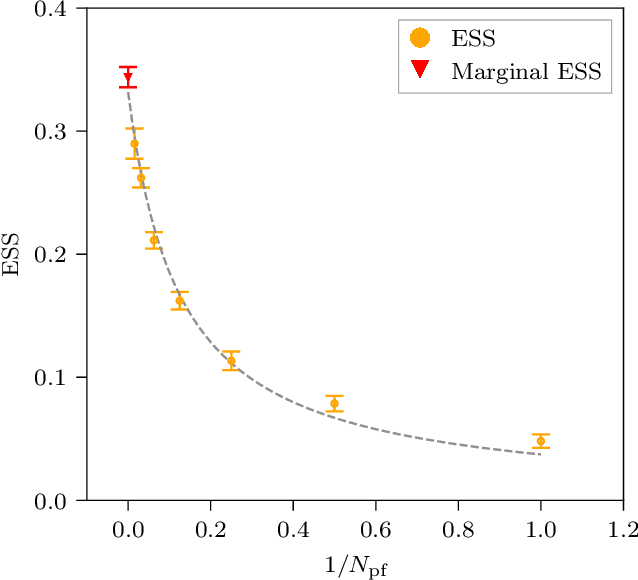
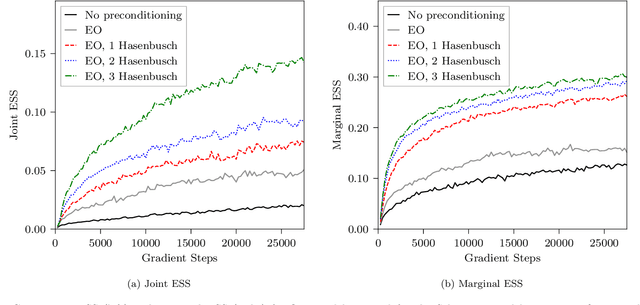
This work presents gauge-equivariant architectures for flow-based sampling in fermionic lattice field theories using pseudofermions as stochastic estimators for the fermionic determinant. This is the default approach in state-of-the-art lattice field theory calculations, making this development critical to the practical application of flow models to theories such as QCD. Methods by which flow-based sampling approaches can be improved via standard techniques such as even/odd preconditioning and the Hasenbusch factorization are also outlined. Numerical demonstrations in two-dimensional U(1) and SU(3) gauge theories with $N_f=2$ flavors of fermions are provided.

Flow-based density of states for complex actions

Emerging sampling algorithms based on normalizing flows have the potential to solve ergodicity problems in lattice calculations. Furthermore, it has been noted that flows can be used to compute thermodynamic quantities which are difficult to access with traditional methods. This suggests that they are also applicable to the density-of-states approach to complex action problems. In particular, flow-based sampling may be used to compute the density directly, in contradistinction to the conventional strategy of reconstructing it via measuring and integrating the derivative of its logarithm. By circumventing this procedure, the accumulation of errors from the numerical integration is avoided completely and the overall normalization factor can be determined explicitly. In this proof-of-principle study, we demonstrate our method in the context of two-component scalar field theory where the $O(2)$ symmetry is explicitly broken by an imaginary external field. First, we concentrate on the zero-dimensional case which can be solved exactly. We show that with our method, the Lee-Yang zeroes of the associated partition function can be successfully located. Subsequently, we confirm that the flow-based approach correctly reproduces the density computed with conventional methods in one- and two-dimensional models.

Flow-based sampling in the lattice Schwinger model at criticality

Recent results suggest that flow-based algorithms may provide efficient sampling of field distributions for lattice field theory applications, such as studies of quantum chromodynamics and the Schwinger model. In this work, we provide a numerical demonstration of robust flow-based sampling in the Schwinger model at the critical value of the fermion mass. In contrast, at the same parameters, conventional methods fail to sample all parts of configuration space, leading to severely underestimated uncertainties.

Flow-based sampling for fermionic lattice field theories

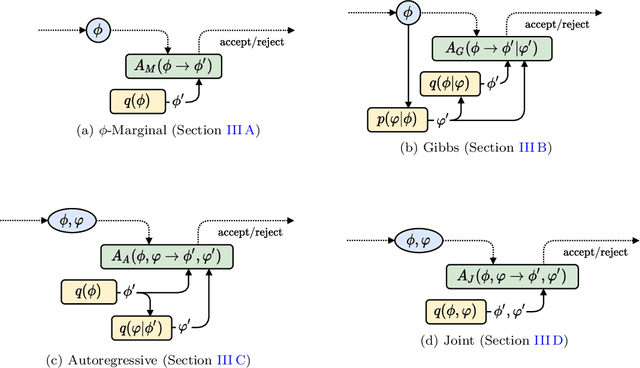
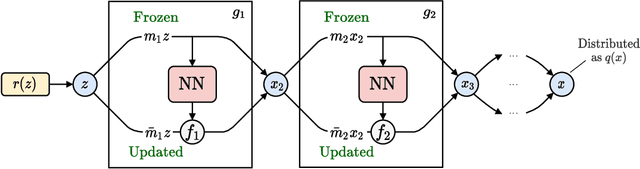
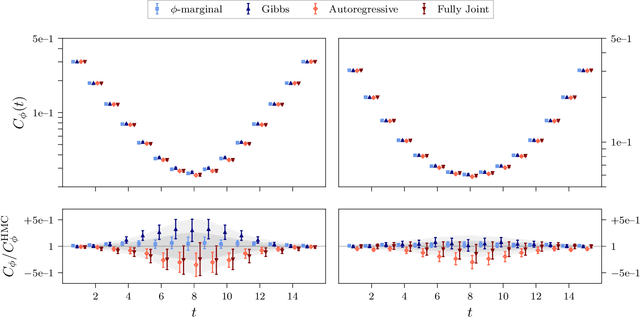
Algorithms based on normalizing flows are emerging as promising machine learning approaches to sampling complicated probability distributions in a way that can be made asymptotically exact. In the context of lattice field theory, proof-of-principle studies have demonstrated the effectiveness of this approach for scalar theories, gauge theories, and statistical systems. This work develops approaches that enable flow-based sampling of theories with dynamical fermions, which is necessary for the technique to be applied to lattice field theory studies of the Standard Model of particle physics and many condensed matter systems. As a practical demonstration, these methods are applied to the sampling of field configurations for a two-dimensional theory of massless staggered fermions coupled to a scalar field via a Yukawa interaction.

Towards Novel Insights in Lattice Field Theory with Explainable Machine Learning

Machine learning has the potential to aid our understanding of phase structures in lattice quantum field theories through the statistical analysis of Monte Carlo samples. Available algorithms, in particular those based on deep learning, often demonstrate remarkable performance in the search for previously unidentified features, but tend to lack transparency if applied naively. To address these shortcomings, we propose representation learning in combination with interpretability methods as a framework for the identification of observables. More specifically, we investigate action parameter regression as a pretext task while using layer-wise relevance propagation (LRP) to identify the most important observables depending on the location in the phase diagram. The approach is put to work in the context of a scalar Yukawa model in (2+1)d. First, we investigate a multilayer perceptron to determine an importance hierarchy of several predefined, standard observables. The method is then applied directly to the raw field configurations using a convolutional network, demonstrating the ability to reconstruct all order parameters from the learned filter weights. Based on our results, we argue that due to its broad applicability, attribution methods such as LRP could prove a useful and versatile tool in our search for new physical insights. In the case of the Yukawa model, it facilitates the construction of an observable that characterises the symmetric phase.

Spectral Reconstruction with Deep Neural Networks

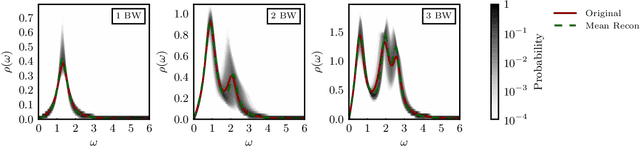
We explore artificial neural networks as a tool for the reconstruction of spectral functions from imaginary time Green's functions, a classic ill-conditioned inverse problem. Our ansatz is based on a supervised learning framework in which prior knowledge is encoded in the training data and the inverse transformation manifold is explicitly parametrised through a neural network. We systematically investigate this novel reconstruction approach, providing a detailed analysis of its performance on physically motivated mock data, and compare it to established methods of Bayesian inference. The reconstruction accuracy is found to be at least comparable, and potentially superior in particular at larger noise levels. We argue that the use of labelled training data in a supervised setting and the freedom in defining an optimisation objective are inherent advantages of the present approach and may lead to significant improvements over state-of-the-art methods in the future. Potential directions for further research are discussed in detail.