Practical applications of machine-learned flows on gauge fields

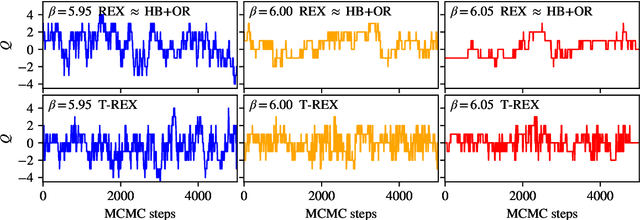
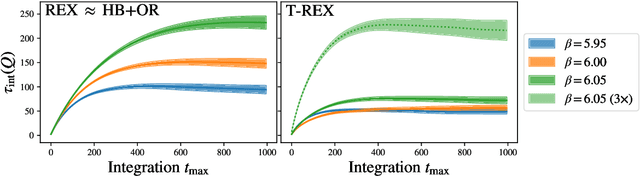
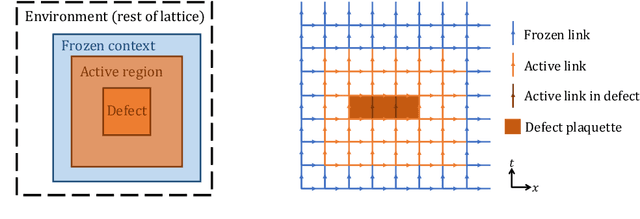
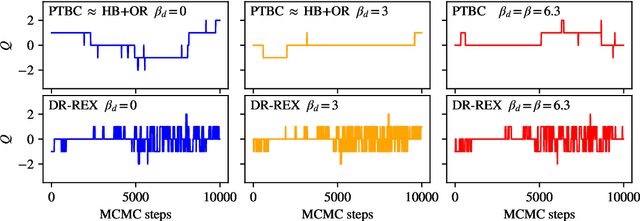
Normalizing flows are machine-learned maps between different lattice theories which can be used as components in exact sampling and inference schemes. Ongoing work yields increasingly expressive flows on gauge fields, but it remains an open question how flows can improve lattice QCD at state-of-the-art scales. We discuss and demonstrate two applications of flows in replica exchange (parallel tempering) sampling, aimed at improving topological mixing, which are viable with iterative improvements upon presently available flows.

Applications of flow models to the generation of correlated lattice QCD ensembles

Machine-learned normalizing flows can be used in the context of lattice quantum field theory to generate statistically correlated ensembles of lattice gauge fields at different action parameters. This work demonstrates how these correlations can be exploited for variance reduction in the computation of observables. Three different proof-of-concept applications are demonstrated using a novel residual flow architecture: continuum limits of gauge theories, the mass dependence of QCD observables, and hadronic matrix elements based on the Feynman-Hellmann approach. In all three cases, it is shown that statistical uncertainties are significantly reduced when machine-learned flows are incorporated as compared with the same calculations performed with uncorrelated ensembles or direct reweighting.

Normalizing flows for lattice gauge theory in arbitrary space-time dimension

Applications of normalizing flows to the sampling of field configurations in lattice gauge theory have so far been explored almost exclusively in two space-time dimensions. We report new algorithmic developments of gauge-equivariant flow architectures facilitating the generalization to higher-dimensional lattice geometries. Specifically, we discuss masked autoregressive transformations with tractable and unbiased Jacobian determinants, a key ingredient for scalable and asymptotically exact flow-based sampling algorithms. For concreteness, results from a proof-of-principle application to SU(3) lattice gauge theory in four space-time dimensions are reported.

Aspects of scaling and scalability for flow-based sampling of lattice QCD

Recent applications of machine-learned normalizing flows to sampling in lattice field theory suggest that such methods may be able to mitigate critical slowing down and topological freezing. However, these demonstrations have been at the scale of toy models, and it remains to be determined whether they can be applied to state-of-the-art lattice quantum chromodynamics calculations. Assessing the viability of sampling algorithms for lattice field theory at scale has traditionally been accomplished using simple cost scaling laws, but as we discuss in this work, their utility is limited for flow-based approaches. We conclude that flow-based approaches to sampling are better thought of as a broad family of algorithms with different scaling properties, and that scalability must be assessed experimentally.

Neural-network preconditioners for solving the Dirac equation in lattice gauge theory

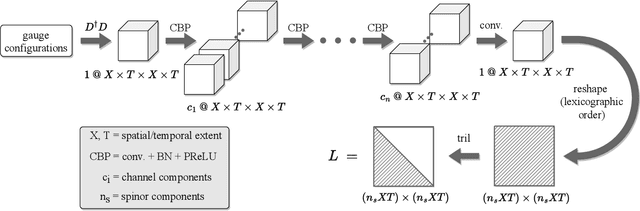
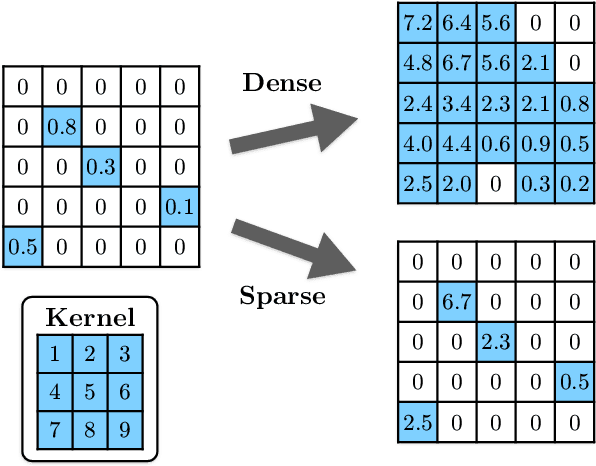
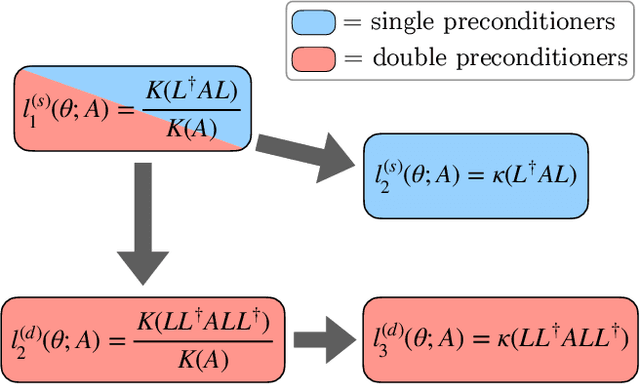
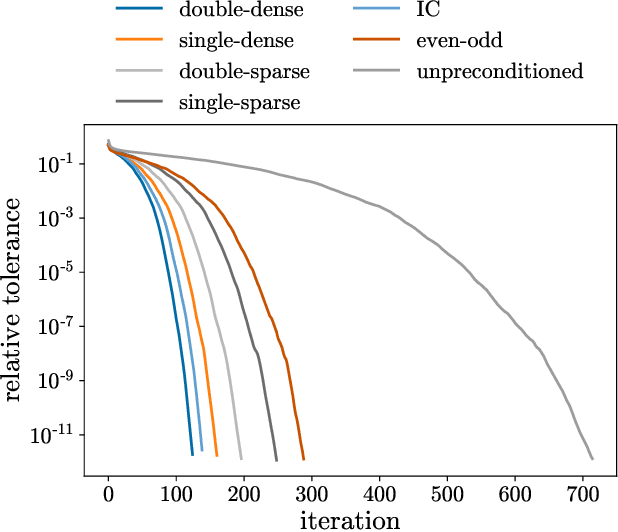
This work develops neural-network--based preconditioners to accelerate solution of the Wilson-Dirac normal equation in lattice quantum field theories. The approach is implemented for the two-flavor lattice Schwinger model near the critical point. In this system, neural-network preconditioners are found to accelerate the convergence of the conjugate gradient solver compared with the solution of unpreconditioned systems or those preconditioned with conventional approaches based on even-odd or incomplete Cholesky decompositions, as measured by reductions in the number of iterations and/or complex operations required for convergence. It is also shown that a preconditioner trained on ensembles with small lattice volumes can be used to construct preconditioners for ensembles with many times larger lattice volumes, with minimal degradation of performance. This volume-transferring technique amortizes the training cost and presents a pathway towards scaling such preconditioners to lattice field theory calculations with larger lattice volumes and in four dimensions.

Gauge-equivariant flow models for sampling in lattice field theories with pseudofermions

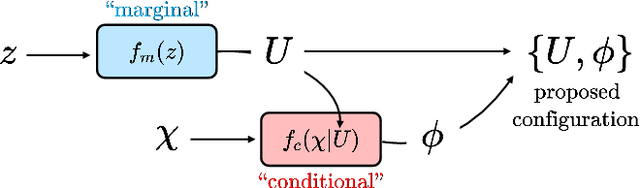
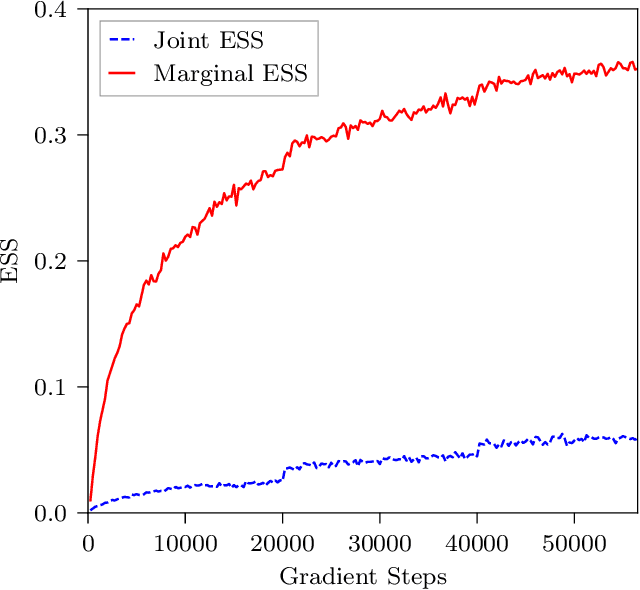
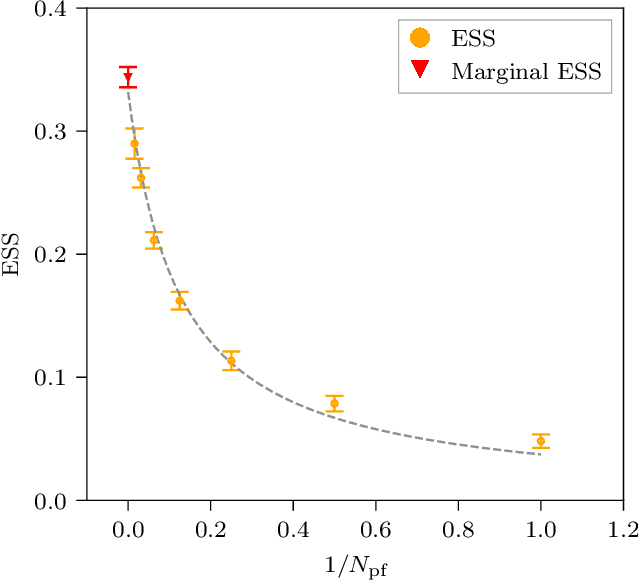
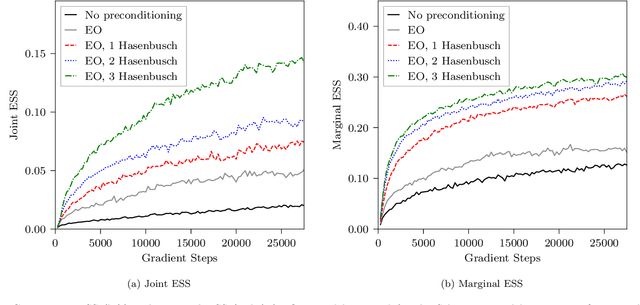
This work presents gauge-equivariant architectures for flow-based sampling in fermionic lattice field theories using pseudofermions as stochastic estimators for the fermionic determinant. This is the default approach in state-of-the-art lattice field theory calculations, making this development critical to the practical application of flow models to theories such as QCD. Methods by which flow-based sampling approaches can be improved via standard techniques such as even/odd preconditioning and the Hasenbusch factorization are also outlined. Numerical demonstrations in two-dimensional U(1) and SU(3) gauge theories with $N_f=2$ flavors of fermions are provided.

Flow-based sampling in the lattice Schwinger model at criticality

Recent results suggest that flow-based algorithms may provide efficient sampling of field distributions for lattice field theory applications, such as studies of quantum chromodynamics and the Schwinger model. In this work, we provide a numerical demonstration of robust flow-based sampling in the Schwinger model at the critical value of the fermion mass. In contrast, at the same parameters, conventional methods fail to sample all parts of configuration space, leading to severely underestimated uncertainties.

Applications of Machine Learning to Lattice Quantum Field Theory

There is great potential to apply machine learning in the area of numerical lattice quantum field theory, but full exploitation of that potential will require new strategies. In this white paper for the Snowmass community planning process, we discuss the unique requirements of machine learning for lattice quantum field theory research and outline what is needed to enable exploration and deployment of this approach in the future.

Flow-based sampling for multimodal distributions in lattice field theory

Recent results have demonstrated that samplers constructed with flow-based generative models are a promising new approach for configuration generation in lattice field theory. In this paper, we present a set of methods to construct flow models for targets with multiple separated modes (i.e. theories with multiple vacua). We demonstrate the application of these methods to modeling two-dimensional real scalar field theory in its symmetry-broken phase. In this context we investigate the performance of different flow-based sampling algorithms, including a composite sampling algorithm where flow-based proposals are occasionally augmented by applying updates using traditional algorithms like HMC.

Flow-based sampling for fermionic lattice field theories

Algorithms based on normalizing flows are emerging as promising machine learning approaches to sampling complicated probability distributions in a way that can be made asymptotically exact. In the context of lattice field theory, proof-of-principle studies have demonstrated the effectiveness of this approach for scalar theories, gauge theories, and statistical systems. This work develops approaches that enable flow-based sampling of theories with dynamical fermions, which is necessary for the technique to be applied to lattice field theory studies of the Standard Model of particle physics and many condensed matter systems. As a practical demonstration, these methods are applied to the sampling of field configurations for a two-dimensional theory of massless staggered fermions coupled to a scalar field via a Yukawa interaction.