Generalizable Equivariant Diffusion Models for Non-Abelian Lattice Gauge Theory

We demonstrate that gauge equivariant diffusion models can accurately model the physics of non-Abelian lattice gauge theory using the Metropolis-adjusted annealed Langevin algorithm (MAALA), as exemplified by computations in two-dimensional U(2) and SU(2) gauge theories. Our network architecture is based on lattice gauge equivariant convolutional neural networks (L-CNNs), which respect local and global symmetries on the lattice. Models are trained on a single ensemble generated using a traditional Monte Carlo method. By studying Wilson loops of various size as well as the topological susceptibility, we find that the diffusion approach generalizes remarkably well to larger inverse couplings and lattice sizes with negligible loss of accuracy while retaining moderately high acceptance rates.

Strategic White Paper on AI Infrastructure for Particle, Nuclear, and Astroparticle Physics: Insights from JENA and EuCAIF

Artificial intelligence (AI) is transforming scientific research, with deep learning methods playing a central role in data analysis, simulations, and signal detection across particle, nuclear, and astroparticle physics. Within the JENA communities-ECFA, NuPECC, and APPEC-and as part of the EuCAIF initiative, AI integration is advancing steadily. However, broader adoption remains constrained by challenges such as limited computational resources, a lack of expertise, and difficulties in transitioning from research and development (R&D) to production. This white paper provides a strategic roadmap, informed by a community survey, to address these barriers. It outlines critical infrastructure requirements, prioritizes training initiatives, and proposes funding strategies to scale AI capabilities across fundamental physics over the next five years.

Physics-Conditioned Diffusion Models for Lattice Gauge Theory

We develop diffusion models for simulating lattice gauge theories, where stochastic quantization is explicitly incorporated as a physical condition for sampling. We demonstrate the applicability of this novel sampler to U(1) gauge theory in two spacetime dimensions and find that a model trained at a small inverse coupling constant can be extrapolated to larger inverse coupling regions without encountering the topological freezing problem. Additionally, the trained model can be employed to sample configurations on different lattice sizes without requiring further training. The exactness of the generated samples is ensured by incorporating Metropolis-adjusted Langevin dynamics into the generation process. Furthermore, we demonstrate that this approach enables more efficient sampling of topological quantities compared to traditional algorithms such as Hybrid Monte Carlo and Langevin simulations.

Physics-Driven Learning for Inverse Problems in Quantum Chromodynamics

The integration of deep learning techniques and physics-driven designs is reforming the way we address inverse problems, in which accurate physical properties are extracted from complex data sets. This is particularly relevant for quantum chromodynamics (QCD), the theory of strong interactions, with its inherent limitations in observational data and demanding computational approaches. This perspective highlights advances and potential of physics-driven learning methods, focusing on predictions of physical quantities towards QCD physics, and drawing connections to machine learning(ML). It is shown that the fusion of ML and physics can lead to more efficient and reliable problem-solving strategies. Key ideas of ML, methodology of embedding physics priors, and generative models as inverse modelling of physical probability distributions are introduced. Specific applications cover first-principle lattice calculations, and QCD physics of hadrons, neutron stars, and heavy-ion collisions. These examples provide a structured and concise overview of how incorporating prior knowledge such as symmetry, continuity and equations into deep learning designs can address diverse inverse problems across different physical sciences.

Random Matrix Theory for Stochastic Gradient Descent

Investigating the dynamics of learning in machine learning algorithms is of paramount importance for understanding how and why an approach may be successful. The tools of physics and statistics provide a robust setting for such investigations. Here we apply concepts from random matrix theory to describe stochastic weight matrix dynamics, using the framework of Dyson Brownian motion. We derive the linear scaling rule between the learning rate (step size) and the batch size, and identify universal and non-universal aspects of weight matrix dynamics. We test our findings in the (near-)solvable case of the Gaussian Restricted Boltzmann Machine and in a linear one-hidden-layer neural network.

Diffusion models learn distributions generated by complex Langevin dynamics

The probability distribution effectively sampled by a complex Langevin process for theories with a sign problem is not known a priori and notoriously hard to understand. Diffusion models, a class of generative AI, can learn distributions from data. In this contribution, we explore the ability of diffusion models to learn the distributions created by a complex Langevin process.

Dyson Brownian motion and random matrix dynamics of weight matrices during learning

During training, weight matrices in machine learning architectures are updated using stochastic gradient descent or variations thereof. In this contribution we employ concepts of random matrix theory to analyse the resulting stochastic matrix dynamics. We first demonstrate that the dynamics can generically be described using Dyson Brownian motion, leading to e.g. eigenvalue repulsion. The level of stochasticity is shown to depend on the ratio of the learning rate and the mini-batch size, explaining the empirically observed linear scaling rule. We verify this linear scaling in the restricted Boltzmann machine. Subsequently we study weight matrix dynamics in transformers (a nano-GPT), following the evolution from a Marchenko-Pastur distribution for eigenvalues at initialisation to a combination with additional structure at the end of learning.

On learning higher-order cumulants in diffusion models

To analyse how diffusion models learn correlations beyond Gaussian ones, we study the behaviour of higher-order cumulants, or connected n-point functions, under both the forward and backward process. We derive explicit expressions for the moment- and cumulant-generating functionals, in terms of the distribution of the initial data and properties of forward process. It is shown analytically that during the forward process higher-order cumulants are conserved in models without a drift, such as the variance-expanding scheme, and that therefore the endpoint of the forward process maintains nontrivial correlations. We demonstrate that since these correlations are encoded in the score function, higher-order cumulants are learnt in the backward process, also when starting from a normal prior. We confirm our analytical results in an exactly solvable toy model with nonzero cumulants and in scalar lattice field theory.

Stochastic weight matrix dynamics during learning and Dyson Brownian motion

We demonstrate that the update of weight matrices in learning algorithms can be described in the framework of Dyson Brownian motion, thereby inheriting many features of random matrix theory. We relate the level of stochasticity to the ratio of the learning rate and the mini-batch size, providing more robust evidence to a previously conjectured scaling relationship. We discuss universal and non-universal features in the resulting Coulomb gas distribution and identify the Wigner surmise and Wigner semicircle explicitly in a teacher-student model and in the (near-)solvable case of the Gaussian restricted Boltzmann machine.

Generative Diffusion Models for Lattice Field Theory

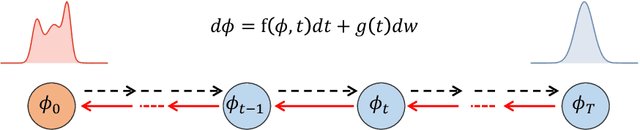
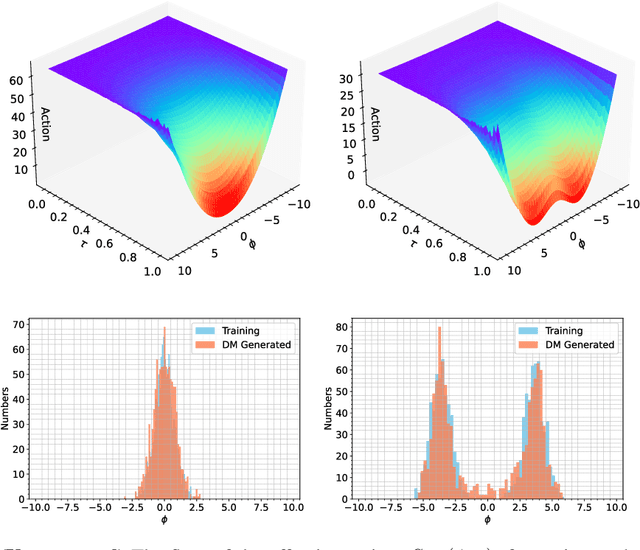
This study delves into the connection between machine learning and lattice field theory by linking generative diffusion models (DMs) with stochastic quantization, from a stochastic differential equation perspective. We show that DMs can be conceptualized by reversing a stochastic process driven by the Langevin equation, which then produces samples from an initial distribution to approximate the target distribution. In a toy model, we highlight the capability of DMs to learn effective actions. Furthermore, we demonstrate its feasibility to act as a global sampler for generating configurations in the two-dimensional $\phi^4$ quantum lattice field theory.