Physics-Driven Learning for Inverse Problems in Quantum Chromodynamics

The integration of deep learning techniques and physics-driven designs is reforming the way we address inverse problems, in which accurate physical properties are extracted from complex data sets. This is particularly relevant for quantum chromodynamics (QCD), the theory of strong interactions, with its inherent limitations in observational data and demanding computational approaches. This perspective highlights advances and potential of physics-driven learning methods, focusing on predictions of physical quantities towards QCD physics, and drawing connections to machine learning(ML). It is shown that the fusion of ML and physics can lead to more efficient and reliable problem-solving strategies. Key ideas of ML, methodology of embedding physics priors, and generative models as inverse modelling of physical probability distributions are introduced. Specific applications cover first-principle lattice calculations, and QCD physics of hadrons, neutron stars, and heavy-ion collisions. These examples provide a structured and concise overview of how incorporating prior knowledge such as symmetry, continuity and equations into deep learning designs can address diverse inverse problems across different physical sciences.

Diffusion models learn distributions generated by complex Langevin dynamics

The probability distribution effectively sampled by a complex Langevin process for theories with a sign problem is not known a priori and notoriously hard to understand. Diffusion models, a class of generative AI, can learn distributions from data. In this contribution, we explore the ability of diffusion models to learn the distributions created by a complex Langevin process.

On learning higher-order cumulants in diffusion models

To analyse how diffusion models learn correlations beyond Gaussian ones, we study the behaviour of higher-order cumulants, or connected n-point functions, under both the forward and backward process. We derive explicit expressions for the moment- and cumulant-generating functionals, in terms of the distribution of the initial data and properties of forward process. It is shown analytically that during the forward process higher-order cumulants are conserved in models without a drift, such as the variance-expanding scheme, and that therefore the endpoint of the forward process maintains nontrivial correlations. We demonstrate that since these correlations are encoded in the score function, higher-order cumulants are learnt in the backward process, also when starting from a normal prior. We confirm our analytical results in an exactly solvable toy model with nonzero cumulants and in scalar lattice field theory.

The Limits and Potentials of Local SGD for Distributed Heterogeneous Learning with Intermittent Communication

Local SGD is a popular optimization method in distributed learning, often outperforming other algorithms in practice, including mini-batch SGD. Despite this success, theoretically proving the dominance of local SGD in settings with reasonable data heterogeneity has been difficult, creating a significant gap between theory and practice. In this paper, we provide new lower bounds for local SGD under existing first-order data heterogeneity assumptions, showing that these assumptions are insufficient to prove the effectiveness of local update steps. Furthermore, under these same assumptions, we demonstrate the min-max optimality of accelerated mini-batch SGD, which fully resolves our understanding of distributed optimization for several problem classes. Our results emphasize the need for better models of data heterogeneity to understand the effectiveness of local SGD in practice. Towards this end, we consider higher-order smoothness and heterogeneity assumptions, providing new upper bounds that imply the dominance of local SGD over mini-batch SGD when data heterogeneity is low.

Pessimistic Value Iteration for Multi-Task Data Sharing in Offline Reinforcement Learning

Offline Reinforcement Learning (RL) has shown promising results in learning a task-specific policy from a fixed dataset. However, successful offline RL often relies heavily on the coverage and quality of the given dataset. In scenarios where the dataset for a specific task is limited, a natural approach is to improve offline RL with datasets from other tasks, namely, to conduct Multi-Task Data Sharing (MTDS). Nevertheless, directly sharing datasets from other tasks exacerbates the distribution shift in offline RL. In this paper, we propose an uncertainty-based MTDS approach that shares the entire dataset without data selection. Given ensemble-based uncertainty quantification, we perform pessimistic value iteration on the shared offline dataset, which provides a unified framework for single- and multi-task offline RL. We further provide theoretical analysis, which shows that the optimality gap of our method is only related to the expected data coverage of the shared dataset, thus resolving the distribution shift issue in data sharing. Empirically, we release an MTDS benchmark and collect datasets from three challenging domains. The experimental results show our algorithm outperforms the previous state-of-the-art methods in challenging MTDS problems. See https://github.com/Baichenjia/UTDS for the datasets and code.

Federated Online and Bandit Convex Optimization

We study the problems of distributed online and bandit convex optimization against an adaptive adversary. We aim to minimize the average regret on $M$ machines working in parallel over $T$ rounds with $R$ intermittent communications. Assuming the underlying cost functions are convex and can be generated adaptively, our results show that collaboration is not beneficial when the machines have access to the first-order gradient information at the queried points. This is in contrast to the case for stochastic functions, where each machine samples the cost functions from a fixed distribution. Furthermore, we delve into the more challenging setting of federated online optimization with bandit (zeroth-order) feedback, where the machines can only access values of the cost functions at the queried points. The key finding here is identifying the high-dimensional regime where collaboration is beneficial and may even lead to a linear speedup in the number of machines. We further illustrate our findings through federated adversarial linear bandits by developing novel distributed single and two-point feedback algorithms. Our work is the first attempt towards a systematic understanding of federated online optimization with limited feedback, and it attains tight regret bounds in the intermittent communication setting for both first and zeroth-order feedback. Our results thus bridge the gap between stochastic and adaptive settings in federated online optimization.

On the Effect of Defections in Federated Learning and How to Prevent Them

Federated learning is a machine learning protocol that enables a large population of agents to collaborate over multiple rounds to produce a single consensus model. There are several federated learning applications where agents may choose to defect permanently$-$essentially withdrawing from the collaboration$-$if they are content with their instantaneous model in that round. This work demonstrates the detrimental impact of such defections on the final model's robustness and ability to generalize. We also show that current federated optimization algorithms fail to disincentivize these harmful defections. We introduce a novel optimization algorithm with theoretical guarantees to prevent defections while ensuring asymptotic convergence to an effective solution for all participating agents. We also provide numerical experiments to corroborate our findings and demonstrate the effectiveness of our algorithm.

Generative Diffusion Models for Lattice Field Theory

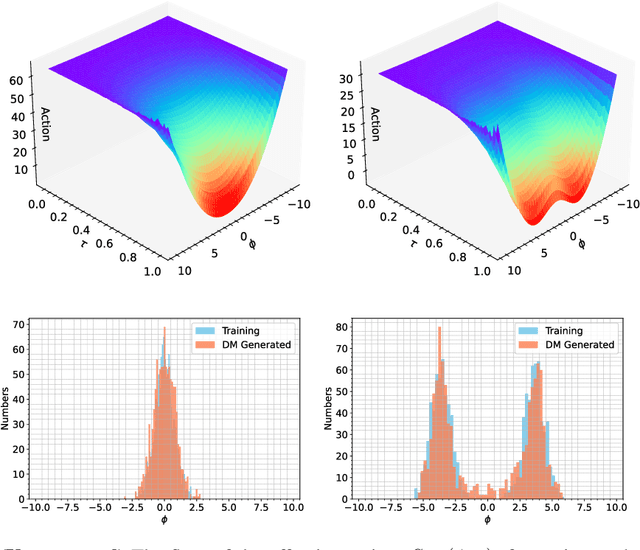
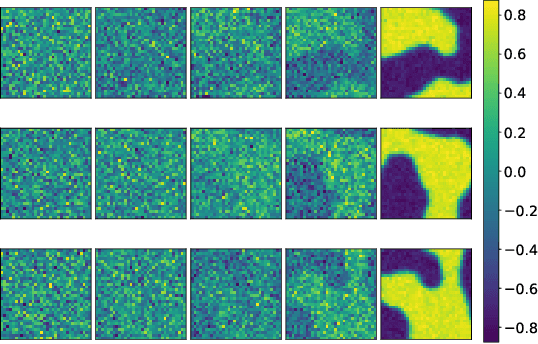
This study delves into the connection between machine learning and lattice field theory by linking generative diffusion models (DMs) with stochastic quantization, from a stochastic differential equation perspective. We show that DMs can be conceptualized by reversing a stochastic process driven by the Langevin equation, which then produces samples from an initial distribution to approximate the target distribution. In a toy model, we highlight the capability of DMs to learn effective actions. Furthermore, we demonstrate its feasibility to act as a global sampler for generating configurations in the two-dimensional $\phi^4$ quantum lattice field theory.

Diffusion Models as Stochastic Quantization in Lattice Field Theory

In this work, we establish a direct connection between generative diffusion models (DMs) and stochastic quantization (SQ). The DM is realized by approximating the reversal of a stochastic process dictated by the Langevin equation, generating samples from a prior distribution to effectively mimic the target distribution. Using numerical simulations, we demonstrate that the DM can serve as a global sampler for generating quantum lattice field configurations in two-dimensional $\phi^4$ theory. We demonstrate that DMs can notably reduce autocorrelation times in the Markov chain, especially in the critical region where standard Markov Chain Monte-Carlo (MCMC) algorithms experience critical slowing down. The findings can potentially inspire further advancements in lattice field theory simulations, in particular in cases where it is expensive to generate large ensembles.

Privileged Knowledge Distillation for Sim-to-Real Policy Generalization

Reinforcement Learning (RL) has recently achieved remarkable success in robotic control. However, most RL methods operate in simulated environments where privileged knowledge (e.g., dynamics, surroundings, terrains) is readily available. Conversely, in real-world scenarios, robot agents usually rely solely on local states (e.g., proprioceptive feedback of robot joints) to select actions, leading to a significant sim-to-real gap. Existing methods address this gap by either gradually reducing the reliance on privileged knowledge or performing a two-stage policy imitation. However, we argue that these methods are limited in their ability to fully leverage the privileged knowledge, resulting in suboptimal performance. In this paper, we propose a novel single-stage privileged knowledge distillation method called the Historical Information Bottleneck (HIB) to narrow the sim-to-real gap. In particular, HIB learns a privileged knowledge representation from historical trajectories by capturing the underlying changeable dynamic information. Theoretical analysis shows that the learned privileged knowledge representation helps reduce the value discrepancy between the oracle and learned policies. Empirical experiments on both simulated and real-world tasks demonstrate that HIB yields improved generalizability compared to previous methods.