Functional Gradient Flows for Constrained Sampling

Recently, through a unified gradient flow perspective of Markov chain Monte Carlo (MCMC) and variational inference (VI), particle-based variational inference methods (ParVIs) have been proposed that tend to combine the best of both worlds. While typical ParVIs such as Stein Variational Gradient Descent (SVGD) approximate the gradient flow within a reproducing kernel Hilbert space (RKHS), many attempts have been made recently to replace RKHS with more expressive function spaces, such as neural networks. While successful, these methods are mainly designed for sampling from unconstrained domains. In this paper, we offer a general solution to constrained sampling by introducing a boundary condition for the gradient flow which would confine the particles within the specific domain. This allows us to propose a new functional gradient ParVI method for constrained sampling, called constrained functional gradient flow (CFG), with provable continuous-time convergence in total variation (TV). We also present novel numerical strategies to handle the boundary integral term arising from the domain constraints. Our theory and experiments demonstrate the effectiveness of the proposed framework.

Semi-Implicit Functional Gradient Flow

Particle-based variational inference methods (ParVIs) use non-parametric variational families represented by particles to approximate the target distribution according to the kernelized Wasserstein gradient flow for the Kullback-Leibler (KL) divergence. Recent works introduce functional gradient flows to substitute the kernel for better flexibility. However, the deterministic updating mechanism may suffer from limited exploration and require expensive repetitive runs for new samples. In this paper, we propose Semi-Implicit Functional Gradient flow (SIFG), a functional gradient ParVI method that uses perturbed particles as the approximation family. The corresponding functional gradient flow, which can be estimated via denoising score matching, exhibits strong theoretical convergence guarantee. We also present an adaptive version of our method to automatically choose the suitable noise magnitude. Extensive experiments demonstrate the effectiveness and efficiency of the proposed framework on both simulated and real data problems.

Kernel Semi-Implicit Variational Inference

Semi-implicit variational inference (SIVI) extends traditional variational families with semi-implicit distributions defined in a hierarchical manner. Due to the intractable densities of semi-implicit distributions, classical SIVI often resorts to surrogates of evidence lower bound (ELBO) that would introduce biases for training. A recent advancement in SIVI, named SIVI-SM, utilizes an alternative score matching objective made tractable via a minimax formulation, albeit requiring an additional lower-level optimization. In this paper, we propose kernel SIVI (KSIVI), a variant of SIVI-SM that eliminates the need for lower-level optimization through kernel tricks. Specifically, we show that when optimizing over a reproducing kernel Hilbert space (RKHS), the lower-level problem has an explicit solution. This way, the upper-level objective becomes the kernel Stein discrepancy (KSD), which is readily computable for stochastic gradient descent due to the hierarchical structure of semi-implicit variational distributions. An upper bound for the variance of the Monte Carlo gradient estimators of the KSD objective is derived, which allows us to establish novel convergence guarantees of KSIVI. We demonstrate the effectiveness and efficiency of KSIVI on both synthetic distributions and a variety of real data Bayesian inference tasks.

Reflected Flow Matching

Continuous normalizing flows (CNFs) learn an ordinary differential equation to transform prior samples into data. Flow matching (FM) has recently emerged as a simulation-free approach for training CNFs by regressing a velocity model towards the conditional velocity field. However, on constrained domains, the learned velocity model may lead to undesirable flows that result in highly unnatural samples, e.g., oversaturated images, due to both flow matching error and simulation error. To address this, we add a boundary constraint term to CNFs, which leads to reflected CNFs that keep trajectories within the constrained domains. We propose reflected flow matching (RFM) to train the velocity model in reflected CNFs by matching the conditional velocity fields in a simulation-free manner, similar to the vanilla FM. Moreover, the analytical form of conditional velocity fields in RFM avoids potentially biased approximations, making it superior to existing score-based generative models on constrained domains. We demonstrate that RFM achieves comparable or better results on standard image benchmarks and produces high-quality class-conditioned samples under high guidance weight.

The Limits and Potentials of Local SGD for Distributed Heterogeneous Learning with Intermittent Communication

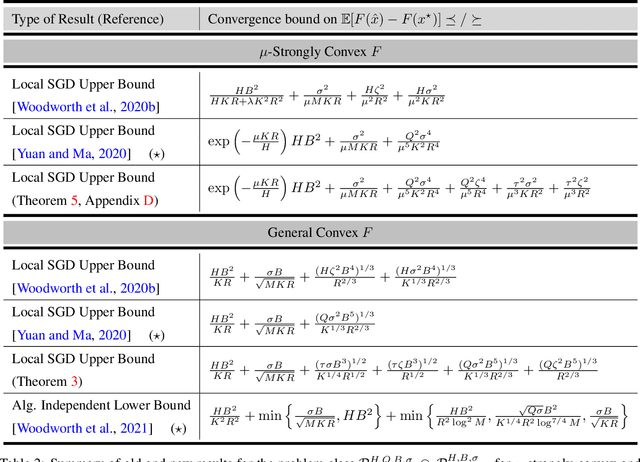
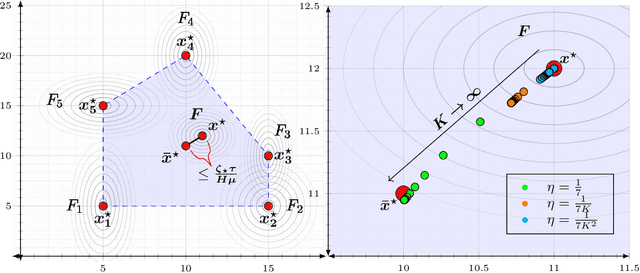
Local SGD is a popular optimization method in distributed learning, often outperforming other algorithms in practice, including mini-batch SGD. Despite this success, theoretically proving the dominance of local SGD in settings with reasonable data heterogeneity has been difficult, creating a significant gap between theory and practice. In this paper, we provide new lower bounds for local SGD under existing first-order data heterogeneity assumptions, showing that these assumptions are insufficient to prove the effectiveness of local update steps. Furthermore, under these same assumptions, we demonstrate the min-max optimality of accelerated mini-batch SGD, which fully resolves our understanding of distributed optimization for several problem classes. Our results emphasize the need for better models of data heterogeneity to understand the effectiveness of local SGD in practice. Towards this end, we consider higher-order smoothness and heterogeneity assumptions, providing new upper bounds that imply the dominance of local SGD over mini-batch SGD when data heterogeneity is low.

SnapCap: Efficient Snapshot Compressive Video Captioning

Video Captioning (VC) is a challenging multi-modal task since it requires describing the scene in language by understanding various and complex videos. For machines, the traditional VC follows the "imaging-compression-decoding-and-then-captioning" pipeline, where compression is pivot for storage and transmission. However, in such a pipeline, some potential shortcomings are inevitable, i.e., information redundancy resulting in low efficiency and information loss during the sampling process for captioning. To address these problems, in this paper, we propose a novel VC pipeline to generate captions directly from the compressed measurement, which can be captured by a snapshot compressive sensing camera and we dub our model SnapCap. To be more specific, benefiting from the signal simulation, we have access to obtain abundant measurement-video-annotation data pairs for our model. Besides, to better extract language-related visual representations from the compressed measurement, we propose to distill the knowledge from videos via a pre-trained CLIP with plentiful language-vision associations to guide the learning of our SnapCap. To demonstrate the effectiveness of SnapCap, we conduct experiments on two widely-used VC datasets. Both the qualitative and quantitative results verify the superiority of our pipeline over conventional VC pipelines. In particular, compared to the "caption-after-reconstruction" methods, our SnapCap can run at least 3$\times$ faster, and achieve better caption results.

Particle-based Variational Inference with Generalized Wasserstein Gradient Flow

Particle-based variational inference methods (ParVIs) such as Stein variational gradient descent (SVGD) update the particles based on the kernelized Wasserstein gradient flow for the Kullback-Leibler (KL) divergence. However, the design of kernels is often non-trivial and can be restrictive for the flexibility of the method. Recent works show that functional gradient flow approximations with quadratic form regularization terms can improve performance. In this paper, we propose a ParVI framework, called generalized Wasserstein gradient descent (GWG), based on a generalized Wasserstein gradient flow of the KL divergence, which can be viewed as a functional gradient method with a broader class of regularizers induced by convex functions. We show that GWG exhibits strong convergence guarantees. We also provide an adaptive version that automatically chooses Wasserstein metric to accelerate convergence. In experiments, we demonstrate the effectiveness and efficiency of the proposed framework on both simulated and real data problems.

Momentum Benefits Non-IID Federated Learning Simply and Provably

Federated learning is a powerful paradigm for large-scale machine learning, but it faces significant challenges due to unreliable network connections, slow communication, and substantial data heterogeneity across clients. FedAvg and SCAFFOLD are two fundamental algorithms to address these challenges. In particular, FedAvg employs multiple local updates before communicating with a central server, while SCAFFOLD maintains a control variable on each client to compensate for "client drift" in its local updates. Various methods have been proposed in literature to enhance the convergence of these two algorithms, but they either make impractical adjustments to algorithmic structure, or rely on the assumption of bounded data heterogeneity. This paper explores the utilization of momentum to enhance the performance of FedAvg and SCAFFOLD. When all clients participate in the training process, we demonstrate that incorporating momentum allows FedAvg to converge without relying on the assumption of bounded data heterogeneity even using a constant local learning rate. This is a novel result since existing analyses for FedAvg require bounded data heterogeneity even with diminishing local learning rates. In the case of partial client participation, we show that momentum enables SCAFFOLD to converge provably faster without imposing any additional assumptions. Furthermore, we use momentum to develop new variance-reduced extensions of FedAvg and SCAFFOLD, which exhibit state-of-the-art convergence rates. Our experimental results support all theoretical findings.

Joint Graph Learning and Model Fitting in Laplacian Regularized Stratified Models

Laplacian regularized stratified models (LRSM) are models that utilize the explicit or implicit network structure of the sub-problems as defined by the categorical features called strata (e.g., age, region, time, forecast horizon, etc.), and draw upon data from neighboring strata to enhance the parameter learning of each sub-problem. They have been widely applied in machine learning and signal processing problems, including but not limited to time series forecasting, representation learning, graph clustering, max-margin classification, and general few-shot learning. Nevertheless, existing works on LRSM have either assumed a known graph or are restricted to specific applications. In this paper, we start by showing the importance and sensitivity of graph weights in LRSM, and provably show that the sensitivity can be arbitrarily large when the parameter scales and sample sizes are heavily imbalanced across nodes. We then propose a generic approach to jointly learn the graph while fitting the model parameters by solving a single optimization problem. We interpret the proposed formulation from both a graph connectivity viewpoint and an end-to-end Bayesian perspective, and propose an efficient algorithm to solve the problem. Convergence guarantees of the proposed optimization algorithm is also provided despite the lack of global strongly smoothness of the Laplacian regularization term typically required in the existing literature, which may be of independent interest. Finally, we illustrate the efficiency of our approach compared to existing methods by various real-world numerical examples.

Motion-aware Dynamic Graph Neural Network for Video Compressive Sensing

Video snapshot compressive imaging (SCI) utilizes a 2D detector to capture sequential video frames and compresses them into a single measurement. Various reconstruction methods have been developed to recover the high-speed video frames from the snapshot measurement. However, most existing reconstruction methods are incapable of capturing long-range spatial and temporal dependencies, which are critical for video processing. In this paper, we propose a flexible and robust approach based on graph neural network (GNN) to efficiently model non-local interactions between pixels in space as well as time regardless of the distance. Specifically, we develop a motion-aware dynamic GNN for better video representation, i.e., represent each pixel as the aggregation of relative nodes under the guidance of frame-by-frame motions, which consists of motion-aware dynamic sampling, cross-scale node sampling and graph aggregation. Extensive results on both simulation and real data demonstrate both the effectiveness and efficiency of the proposed approach, and the visualization clearly illustrates the intrinsic dynamic sampling operations of our proposed model for boosting the video SCI reconstruction results. The code and models will be released to the public.